Diffusion은 신이고 GPT는 무적이다

ICLR 2022. [Paper] [Github]
Max W. Y. Lam, Jun Wang, Dan Su, Dong Yu
Tencent AI Lab
25 Mar 2022

Introduction

Likelihood 기반 모델의 최신 클래스는 diffusion probabilistic model (DPM)로, forward diffusion process를 사용하여 주어진 분포를 순차적으로 손상시키고 이러한 diffusion process의 역을 학습하여 데이터 분포를 복원한다. 샘플링을 위해. 유사한 관점에서 Langevin dynamics를 통해 샘플이 생성될 수 있도록 신경망을 학습시키기 위해 score matching 기법을 적용하여 score 기반 생성 모델도 제안되었다. 이 두 가지 연구 라인을 따라 고품질 이미지 합성을 위한 DDPM이 제안되었다. Improved DDPM은 SOTA GAN 기반 모델에 필적하거나 더 우수한 품질의 고품질 이미지를 생성할 수 있다. 음성 합성의 경우 Wavegrad와 DiffWave에도 DDPM을 적용하여 기존의 non-autoregressive model보다 충실도가 높은 오디오 샘플을 생성하고 SOTA autoregressive 방법의 품질과 일치했다.

설득력 있는 결과에도 불구하고 diffusion model은 GAN이나 VAE와 같은 다른 생성 모델보다 2~3배 더 느리다. 주요 제한 사항은 대상 분포를 학습하기 위해 학습 중에 최대 수천 개의 diffusion step이 필요하다는 것이다. 따라서 샘플링 시간에 많은 reverse step이 필요한 경우가 많다.

최근에 고품질 샘플을 효율적으로 생성하기 위한 샘플링 step을 줄이기 위한 광범위한 연구가 수행되었다. 특이하게도, 저자들은 기존의 diffusion model과 비슷하거나 더 우수한 생성 성능을 달성하면서 샘플링을 위한 훨씬 더 짧은 noise schedule을 효율적이고 적응적으로 추정하도록 신경망을 학습시킬 수 있다고 생각했다.

본 논문은 기존 diffusion model을 도입한 후 양방향 모델링 관점에서 이름을 딴 Bilateral Denoising Diffusion Models (BDDM)을 제안한다. Forward process와 reverse process를 각각 schedule network와 score network로 parameterize한다. 저자들은 이론적으로 score network가 최적화된 후에 schedule network가 학습되어야 한다고 추론하였다.

Schedule network를 학습하기 위해 새로 파생된 하한과 log marginal likelihood 사이의 간격을 최소화하는 새로운 목적 함수를 제안하였다. Schedule network의 학습은 새로 파생된 목적 함수를 사용하여 매우 빠르게 수렴되며 해당 학습은 DDPM에 무시할 수 있는 오버헤드만 추가한다. 저자들은 BDDM이 최소 3개의 샘플링 step으로 고충실도 샘플을 생성할 수 있음을 보여주었다. 또한 단 7개의 샘플링 step만으로 인간의 음성과 구별할 수 없는 음성 샘플을 생성할 수 있다. (WaveGrad보다 143배 빠르고 DiffWave보다 28.6배 빠름)

Bilateral Denoising Diffusion Models (BDDMs)

1. Problem Formulation


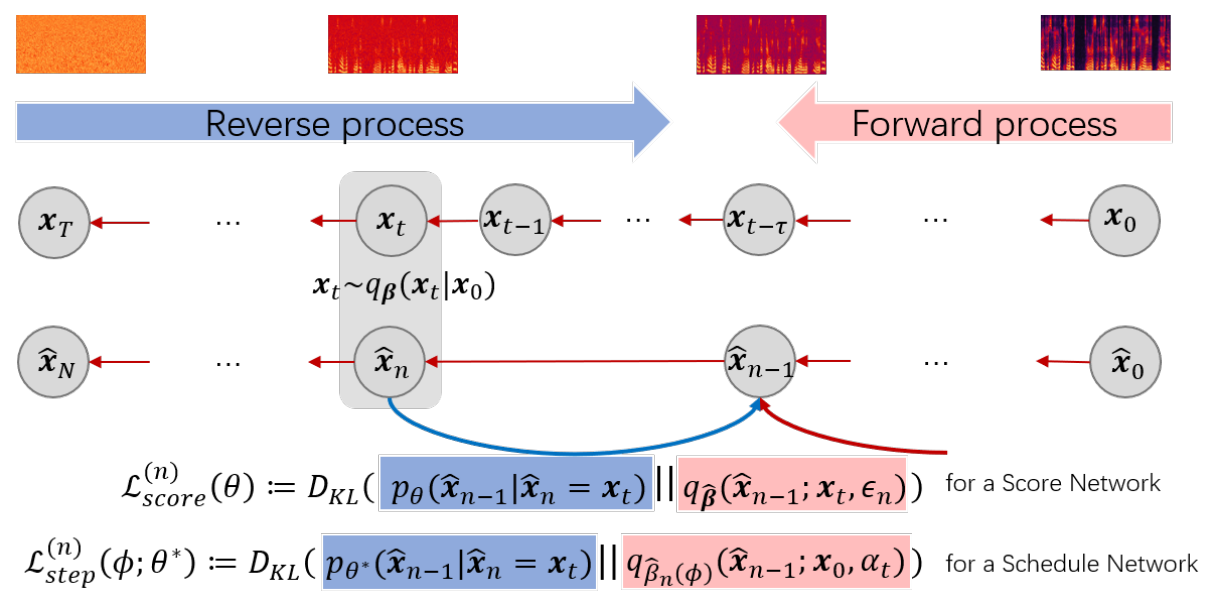
Diffusion model을 사용한 빠른 샘플링을 위해 학습을 위한 noise schedule $\beta$보다 훨씬 짧은 샘플링을 위한 noise schedule $\hat{\beta}$을 사용한다. 위 그림에서 볼 수 있듯이 noise schedule에 해당하는 두 개의 개별 diffusion process인 $\beta$와 $\hat{\beta}$를 각각 정의한다. $\beta$로 parameterize된 upper diffusion process는

\[\begin{equation} q_\beta (x_{1:T} \vert x_0) := \prod_{t=1}^T q_{\beta_t} (x_t \vert x_{t-1}) \\ q_{\beta_t} (x_t \vert x_{t-1}) := \mathcal{N} (\sqrt{1- \beta_t} x_{t-1}, \beta_t I) \end{equation}\]

와 동일하지만 lower process는 훨씬 적은 diffusion step으로 정의된다.

\[\begin{equation} q_{\hat{\beta}} (\hat{x}_{1:N} \vert \hat{x}_0) = \prod_{n=1}^N q_{\hat{\beta}_n} (\hat{x}_n \vert \hat{x}_{n-1}) \quad (N \ll T) \end{equation}\]

$\beta$는 주어지지만 $\hat{\beta}$는 모른다. Reverse process \(p_\theta (\hat{x}_{n-1} \vert \hat{x}^n; \hat{\beta}_n)\)에 대한 $\hat{\beta}$를 찾아 \(\hat{x}_0\)가 \(\hat{x}_N\)에서 N개의 reverse step으로 효과적으로 복구될 수 있도록 하는 것이 목표다.

2. Model Description

많은 이전 연구들이 단축된 linear 또는 Fibonacci noise schedule을 reverse process에 직접 적용했지만, 저자들은 이것이 최선이 아니라고 주장한다. 이론적으로 새로운 단축된 noise schedule에 의해 지정된 diffusion process는 score network $\theta$를 학습하는 데 사용되는 프로세스와 본질적으로 다르다. 따라서 $\theta$는 단축된 diffusion process를 되돌리기에 적합하다고 보장할 수 없다. 이 문제는 단축된 schedule $\hat{\beta}$와 score network $\theta$ 사이의 연결을 설정하기 위해, 즉 $\theta$에 따라 $\hat{\beta}$를 최적화하도록 새로운 모델링 관점에 동기를 부여했다.

시작점으로 $\lfloor N = T / \tau \rfloor$를 고려한다. 여기서 $1 \le \tau < T$는 더 짧은 diffusion process에서 두 연속 변수 사이의 각 diffusion step이 더 긴 diffusion process에서 $\tau$개의 diffusion step에 해당하도록 step 크기를 제어하는 hyperparameter이다. 다음과 같이 정의한다.

\[\begin{aligned} q_{\hat{\beta}_{n+1}} (\hat{x}_{n+1} \vert \hat{x}_n = x_t) &:= q_\beta (x_{t + \tau} \vert x_t) \\ &= \mathcal{N} \bigg( \sqrt{\frac{\alpha_{t+\tau}^2}{\alpha_t^2}} x_t, \bigg( 1 - \frac{\alpha_{t+\tau}^2}{\alpha_t^2} \bigg) I \bigg) \end{aligned}\]

여기서 $x_t$는 두 개의 서로 다르게 인덱싱된 diffusion 시퀀스를 연결하기 위해 도입한 중간 diffusion 변수이다. 이 변수를 junctional variable라고 부르면, 학습 중에 $x_0$와 $\beta$가 주어지면 쉽게 생성할 수 있다.

\[\begin{equation} x_t = \alpha_t x_0 + \sqrt{1 - \alpha_t^2} \epsilon_n \end{equation}\]

불행하게도, $x_0$이 주어지지 않을 때의 reverse process에 대해 junctional variable은 tractable하지 않다. 그러나 긴 $\beta$로 parameterize된 diffusion process에 대해 학습된 score network $\theta^\ast$에 의해 score를 사용하는 동안 schedule network $\phi$를 도입하여 그에 따라 짧은 noise schedule $\hat{\beta} (\phi)$를 최적화할 수 있다.

3. Score Network

DDPM은 white noise $x_T \sim \mathcal{N}(0,I)$에서 reverse process를 시작하고 데이터 분포를 복구하기 위해 $T$ step을 수행한다.

\[\begin{equation} p_\theta (x_0) := \mathbb{E}_{\mathcal{N}(0,I)} [\mathbb{E}_{p_\theta (x_{1:T-1} \vert x_T)} [p_\theta (x_0 \vert x_{1:T})]] \end{equation}\]

대조적으로 BDDM은 junctional variable $x_t$에서 시작하여 단 $n$개의 step으로 더 짧은 diffusion 확률 변수 시퀀스를 되돌린다.

\[\begin{equation} p_\theta (\hat{x}_0) := \mathbb{E}_{q_{\hat{\beta}} (\hat{x}_{n-1}; x_t, \epsilon_n)} [\mathbb{E}_{p_\theta (\hat{x}_{1:n-2} \vert \hat{x}_{n-1})} [p_\theta (x_0 \vert x_{1:n-1})]], \quad 2 \le n \le N \end{equation}\]

여기서 \(q_{\hat{\beta}} (\hat{x}_{n-1}; x_t, \epsilon_n)\)는 posterior에 대한 re-parameterization으로 정의된다.

\[\begin{aligned} q_{\hat{\beta}} (\hat{x}_{n-1}; x_t, \epsilon_n) &:= q_{\hat{\beta}} \bigg( \hat{x}_{n-1} \vert \hat{x}_n = x_t, \hat{x}_0 = \frac{x_t - \sqrt{1 - \hat{\alpha}_n^2} \epsilon_n}{\hat{\alpha}_n} \bigg) \\ &= \mathcal{N} \bigg( \frac{1}{\sqrt{1 - \hat{\beta}_n}} x_t - \frac{\hat{\beta}_n}{\sqrt{(1 - \hat{\beta}_n)(1 - \hat{\alpha}_n^2)}} \epsilon_n, \frac{1 - \hat{\alpha}_{n-1}^2}{1 - \hat{\alpha}_n^2} \hat{\beta}_n I \bigg) \end{aligned}\] \[\begin{equation} \hat{\alpha}_n = \prod_{i=1}^n \sqrt{1 - \hat{\beta}_i}, \quad x_t = \alpha_t x_0 + \sqrt{1 - \alpha_t^2} \epsilon_n \end{equation}\]

여기서 $x_t$는 근사 인덱스 \(t \sim \mathcal{U}\{(n − 1) \tau, \cdots, n \tau − 1, n \tau\}\)가 주어졌을 때 $x_t$를 $\hat{x}_n$에 매핑하는 junctional variable이다.

Training objective for score network

위의 정의를 통해 log marginal likelihood에 대한 새로운 형태의 하한은 다음과 같이 유도될 수 있다.

\[\begin{aligned} \log p_\theta (\hat{x}_0) \ge \mathcal{F}_\textrm{score}^{(n)} (\theta) &:= − \mathcal{L}_\textrm{score}^{(n)} (\theta) − \mathcal{R}_\theta (\hat{x}_0, x_t) \\ \mathcal{L}_\textrm{score}^{(n)} (\theta) &:= D_\textrm{KL} (p_\theta (\hat{x}_{n-1} \vert \hat{x}_n = x_t) \| q_{\hat{\beta}} (\hat{x}_{n-1}; x_t, \epsilon_n)) \\ \mathcal{R}_\theta (\hat{x}_0, x_t) &:= - \mathbb{E}_{p_\theta (\hat{x}_1 \vert \hat{x}_n = x_t)} [\log p_\theta (\hat{x}_0 \vert \hat{x}_1)] \end{aligned}\]

Junctional variable $x_t$를 통해 목적 함수 \(\mathcal{L}_\textrm{ddpm}^{(t)} (\theta), \forall t \in \{1, \cdots, T\}\)를 최적화하는 해 $\theta^\ast$가 \(\mathcal{L}_\textrm{score}^{(n)} (\theta), \forall n \in \{2, \cdots, N\}\)을 최적화하는 해이기도 하다. 따라서 score network $\theta$가 \(\mathcal{L}_\textrm{ddpm}^{(t)} (\theta)\)로 학습되고 \(\hat{x}_{N:0}\)에 대한 짧은 diffusion process를 되돌리기 위해 재사용될 수 있다. 새로 도출된 하한은 기존 score network와 동일한 목적 함수로 결과가 나왔지만 처음으로 score network $\theta$와 \(\hat{x}_{N:0}\) 사이의 연결을 설정한다.

4. Schedule Network

BDDM에서는 $\hat{\beta}_n$을

\[\begin{equation} \hat{\beta}_n (\phi) = f_\phi (x_t; \hat{\beta}_{n+1}) \end{equation}\]

로 다시 parameterize하여 forward process에 schedule network를 도입한다. Re-parameterization을 통해 noise schedule의 task, 즉 $\hat{\beta}$ 검색은 이제 데이터 종속 분산을 추정하는 schedule network $f_\phi$를 학습하는 것으로 재구성될 수 있다. Schedule network는 현재 noisy한 샘플 $x_t$를 기반으로 \(\hat{\beta}_n\)을 예측하는 방법을 학습한다. Diffusion step 정보를 반영하는 \(\hat{\beta}_{n+1}\), $t$, $n$ 외에도 $x_t$는 inference 시에 reverse 방향에서의 noise schedule에 필수적이다.

구체적으로, ancestral step 정보 (\(\hat{\beta}_{n+1}\))를 채택하여 현재 step에 대한 상한값을 도출하는 한편 schedule network는 현재 $x_t$를 입력으로만 남겨 ancestral step에 대한 noise scale의 상대적인 변화를 예측한다.

먼저, \(\hat{\beta}_n\)의 상한값은 다음과 같다.

\[\begin{equation} 0 < \hat{\beta}_n < \min \bigg\{ 1 - \frac{\hat{\alpha}_{n+1}^2}{1 - \hat{\beta}_{n+1}}, \hat{\beta}_{n+1} \bigg\} \end{equation}\]

그런 다음 신경망 $\sigma_\phi : \mathbb{R}^D \mapsto (0,1)$에 의해 추정된 비율로 상한선을 곱하여 다음을 정의한다.

\[\begin{equation} f_\phi (x_t; \hat{\beta}_{n+1}) := \min \bigg\{ 1 - \frac{\hat{\alpha}_{n+1}^2}{1 - \hat{\beta}_{n+1}}, \hat{\beta}_{n+1} \bigg\} \sigma_\phi (x_t) \end{equation}\]

여기서 파라미터 $\phi$는 현재 $x_t$에서 두 개의 연속 noise scale (\(\hat{\beta}_n\)과 \(\hat{\beta}_{n+1}\)) 사이의 비율을 추정하기 위해 학습된다.

마지막으로 noise schedule을 위한 inference 시에 최대 reverse step ($N$)과 두 개의 hyperparameter $(\hat{\alpha}_N, \hat{\beta}_N)$에서 시작하여 noise scale \(\hat{\beta}_n (\phi) = f_\phi (\hat{x}_n; \hat{\beta}_{n+1})\)으로 예측하고, 누적하여 곱

\[\begin{equation} \hat{\alpha}_n = \frac{\hat{\alpha}_{n+1}}{\sqrt{1 - \hat{\beta}_{n+1}}} \end{equation}\]

를 업데이트한다.

Algorithms: Training, Noise Scheduling, and Sampling

Experiments

1. Sampling quality in objective and subjective metrics

다음은 BDDM을 SOTA vocoder와 비교한 표이다.


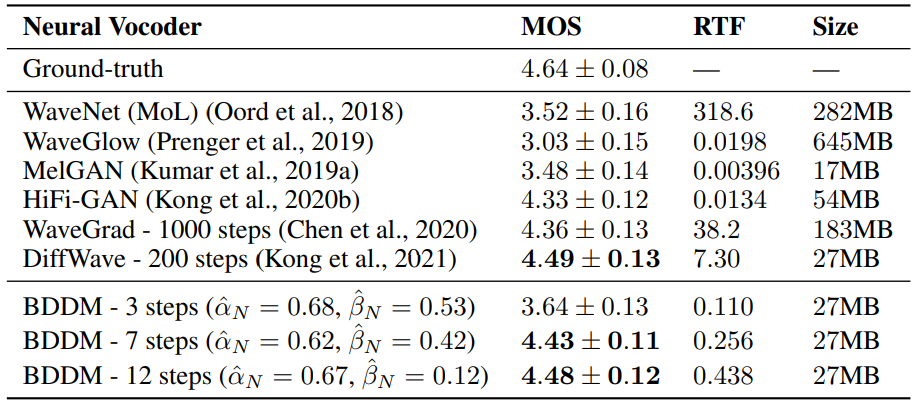
다음은 동일한 score network와 동일한 step 수로 BDDM을 샘플링 가속화 방법들과 비교한 것이다.

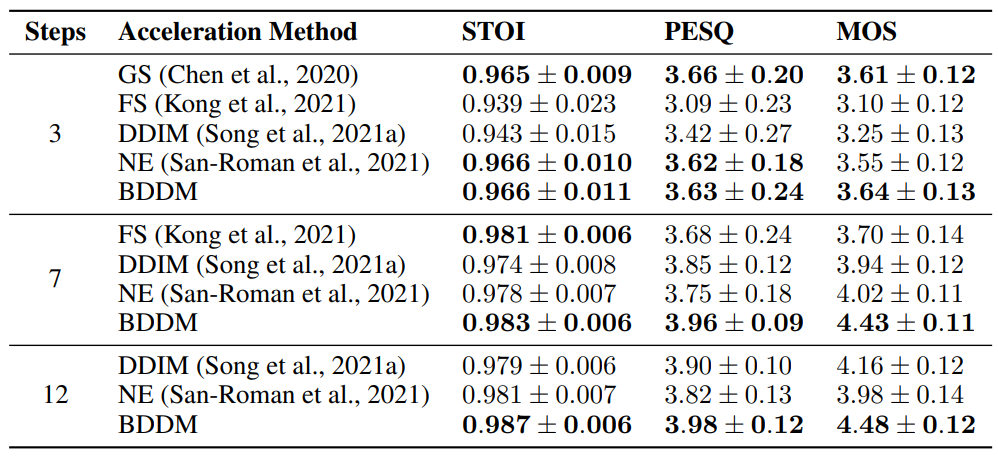
2. Ablation study and analysis

BDDM의 주요 이점은 $\phi$를 학습하기 위해 새로 파생된 목적 함수 \(\mathcal{L}_\textrm{step}^{(n)}\)에 있다. 저자들은 이에 대한 더 나은 이유를 찾기 위해 제안된 loss를 표준 negative ELBO로 대체하는 ablation study를 수행했다.


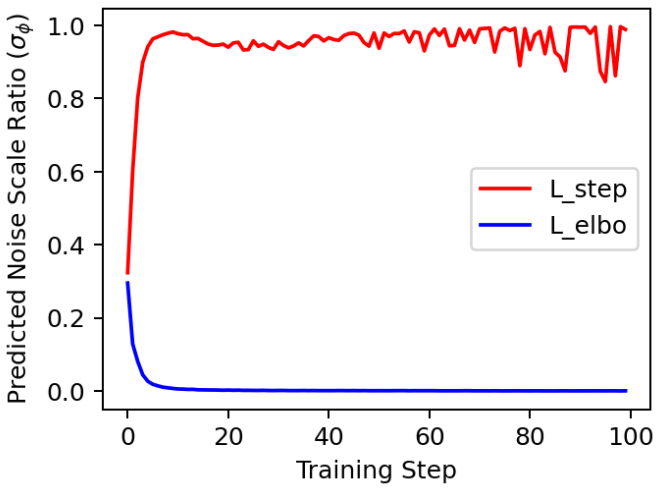
위 그래프는 학습 loss가 다른 네트워크 출력을 plot한 것이다. \(\mathcal{L}_\textrm{elbo}^{(n)}\)를 사용하여 $\phi$를 학습할 때 네트워크 출력이 여러 학습 step 내에서 빠르게 0으로 붕괴되는 것으로 나타났다. 반면 \(\mathcal{L}_\textrm{elbo}^{(n)}\)로 학습된 네트워크는 변동하는 출력을 생성했다. 변동은 네트워크가 $t$에 종속된 noise scale을 적절하게 예측한다는 것을 보여주는 바람직한 속성이다. $t$는 균일한 분포에서 가져온 임의의 timestep이기 때문이다.

저자들은 $\hat{\beta} = \beta$로 설정하고 최적화된 $\theta^\ast$를 동일하게 사용하여

\[\begin{equation} \mathcal{F}_\textrm{bddm}^{(t)} := \mathcal{F}_\textrm{score}^{(t)} + \mathcal{L}_\textrm{step}^{(t)} \ge \mathcal{F}_\textrm{elbo}^{(t)} \end{equation}\]

가 $t \in [20, 180]$에서 각각의 값을 갖는지 경험적으로 검증했다.


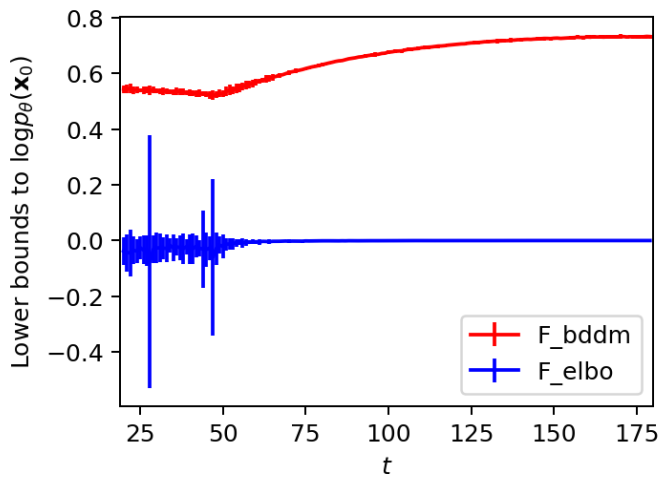
각 값은 위 그래프와 같다 (95% 신뢰 구간). 그래프는 본 논문이 제안한 경계 \(\mathcal{F}_\textrm{bddm}^{(t)}\)이 항상 모든 $t$에서 표준 경계보다 더 엄격한 하한임을 보여준다. 더욱이 \(\mathcal{F}_\textrm{bddm}^{(t)}\)가 $t \le 50$에 대해 상대적으로 훨씬 더 낮은 분산으로 낮은 값을 얻었음을 알 수 있다. 여기서 \(\mathcal{F}_\textrm{elbo}^{(t)}\)는 변동성이 매우 컸다. 이것은 \(\mathcal{F}_\textrm{bddm}^{(t)}\)이 어려운 학습 부분, 즉 score가 $t \rightarrow 0$으로 추정하기 더 어려워질 때 더 잘 해결한다는 것을 의미한다.

You may also enjoy