[논문리뷰] BillBoard Splatting (BBSplat): Learnable Textured Primitives for Novel View Synthesis

ICCV 2025. [Paper] [Page] [Github]
David Svitov, Pietro Morerio, Lourdes Agapito, Alessio Del Bue
Universita degli Studi di Genova | Istituto Italiano di Tecnologia (IIT) | University College London
13 Nov 2024

Introduction

최근 2D Gaussian Splatting (2DGS)은 3D 방향으로 배치된 평면 Gaussian을 사용하는 것을 제안했다. 2D Gaussian은 물체 표면에 실질적으로 접하기 때문에 더 정확한 표면 추출이 가능하다. 메쉬 추출 task에서 2D primitive는 효율성을 입증했지만, 3D Gaussian과 같은 3D primitive에 비해 렌더링 지표가 저하된다. 본 논문에서는 새로운 primitive 표현 방식을 도입하여 2D primitive를 고품질 novel view synthesis(NVS)에 적합하게 만드는 동시에 안정적인 메쉬 추출을 가능하게 하는 것을 목표로 하였다.

제안된 primitive는 극단적인 3D 모델 단순화에 사용되는 고전적인 billboard에서 영감을 얻었다. 알파 채널을 가진 텍스처가 적용된 평면 primitive의 “billboard cloud”를 사용하여 3D 장면을 효율적으로 렌더링할 수 있다. Billboard를 사용하면 벽이나 장면 배경의 그림과 같은 평면 표면을 효율적으로 모델링할 수 있으며, 필요한 primitive 수를 3DGS/2DGS에 비해 최대 10배까지 크게 줄일 수 있다.

2D Gaussian 파라미터 (rotation, scaling, 3D 중심 위치, spherical harmonics)를 사용하여 billboard를 정의하는 동시에, 픽셀 단위의 색상과 모양을 제어하기 위해 RGB 텍스처와 alpha map을 도입했다. alpha map은 billboard 실루엣을 정의하고 primitive의 임의의 모양을 모델링한다. 마찬가지로, RGB 텍스처는 billboard의 각 지점에 대한 색상을 저장한다. 이러한 방식으로 고주파 디테일을 표현하는 데 더 적은 primitive를 사용할 수 있다. 본 접근법의 핵심은 BillBoard Splatting (BBSplat)으로, 이미지 집합으로부터 billboard 파라미터를 학습한다.

모든 billboard 텍스처를 저장하는 과제를 해결하기 위해, 각 텍스처를 spherical harmonics (SH)로 계산된 색상으로부터 sparse offset으로 표현하고 8비트로 추가 quantization하여 텍스처를 압축한다. 그러면 quantization된 텍스처에 dictionary 기반 압축 알고리즘을 효율적으로 활용할 수 있다.

Method

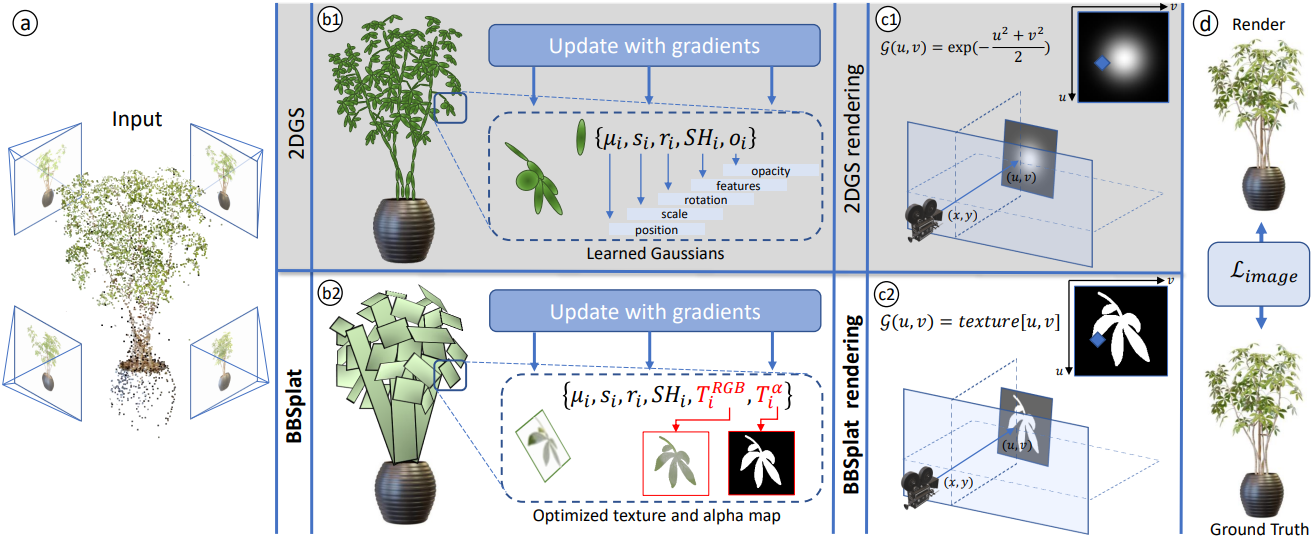
1. Billboard Splatting

Billboard primitive는 평면을 기반으로 하지만 색상과 투명도를 계산하기 위해 Gaussian 분포를 활용하는 대신 학습 가능한 텍스처를 활용한다. 이러한 평면에 대한 2DGS parametrization \(\{\mu_i, s_i, r_i, \textrm{SH}_i\}\)을 상속한다. Gaussian 불투명도 $o_i$를 사용하는 대신 평면의 각 지점에서 투명도를 텍스처 $$T_i^\alpha$로 설정한다. 이렇게 하면 각 billboard가 임의의 모양을 가질 수 있다. 또한, billboard의 모든 지점의 색상을 제어하기 위해 RGB 텍스처인 $T_i^\textrm{RGB}$를 사용한다.

명시적인 광선-splat 교차 알고리즘을 사용하여 화면 좌표 $\textbf{x} = (x, y)^\top$에 대한 해당 평면 좌표 $\textbf{u} = (u, v)^\top$를 구한다. 구체적으로, 카메라 광선을 두 개의 4D homogeneous plane \(\textbf{h}_x = (−1, 0, 0, x)^\top\)와 \(\textbf{h}_y = (0, -1, 0, y)^\top\)의 교차점으로 parametrize한다. 그런 다음, 이 평면들을 평면 $H$의 $uv$ 좌표계로 변환하여 $(u, v)$ 좌표에서 교차점을 구한다.

\[\begin{equation} \textbf{h}_u = (WH)^\top \textbf{h}_x \quad \textbf{h}_v = (WH)^\top \textbf{h}_y \end{equation}\]

($W \in \mathbb{R}^{4 \times 4}$는 world space에서 screen space로의 transformation matrix)

그러면 교차점의 $(u, v)$ 좌표를 다음과 같이 계산한다.

\[\begin{equation} \textbf{u}(x) = \frac{\textbf{h}_u^2 \textbf{h}_v^4 - \textbf{h}_u^4 \textbf{h}_v^2}{\textbf{h}_u^1 \textbf{h}_v^2 - \textbf{h}_u^2 \textbf{h}_v^1} \quad \textbf{v}(x) = \frac{\textbf{h}_u^4 \textbf{h}_v^1 - \textbf{h}_u^1 \textbf{h}_v^4}{\textbf{h}_u^1 \textbf{h}_v^2 - \textbf{h}_u^2 \textbf{h}_v^1} \end{equation}\]

(\(\textbf{h}_u^i\)와 \(\textbf{h}_u^i\)는 4D homogeneous plane 파라미터의 $i$번째 값)

이렇게 하면 평면 중심 \(\mu_i\)가 0이 되는 $[-1, 1]$ 범위 내의 $(u, v)$ 좌표를 얻는다. 그 후, 이 좌표들을 $[0; S_T]$ 범위로 rescaling한다. 여기서 $S_T$는 texel의 텍스처 크기에 해당한다. Rescaling된 $(u, v)$ 좌표를 사용하여 광선-splat 교차점의 색상과 불투명도를 샘플링하고 광선을 따라 다음과 같이 누적한다.

\[\begin{equation} c(x) = \sum_{i=1} c_i [\textbf{u}(x)] T_i^\alpha [\textbf{u}(x)] \prod_{j=1}^{i-1} (1 - T_j^\alpha [\textbf{u}(x)]) \end{equation}\]

여기서 $c_i$는 \(\textrm{SH}_i\)와 샘플링된 색상 \(T_i^\textrm{RGB} [\textbf{u}(x)]\)로 계산된 view-dependent한 색상이다. 텍스처 값 $T[\cdot]$를 샘플링하기 위해 bilinear sampling을 사용한다. 이를 통해 인접 texel을 고려하여 텍스처를 기준으로 billboard 위치 \(\mu_i\)에 대한 gradient를 계산할 수 있다. 즉, 샘플링된 값에 기여한 texel 간에 입력 gradient 값을 기여 가중치에 따라 재분배한다.

$i$번째 billboard의 각 $uv$-포인트 $\textbf{u}$에서 view-dependent한 색상 $c_i$의 값을 계산하기 위해 샘플링된 텍스처 색상 \(T_i^\textrm{RGB} [\textbf{u}]\)를 SHi와 뷰 방향 벡터 \(\textbf{d}_i\)로 예측된 ​​색상에 대한 offset으로 통합한다.

\[\begin{equation} c_i [\textbf{u}] = T_i^\textrm{RGB}[\textbf{u}] + \textrm{RGB} (\textrm{SH}_i, \textbf{d}_i) \end{equation}\]

(\(\textbf{d}_i\)는 카메라 위치에서 billboard 중심 위치 \(\mu_i\)까지의 뷰 방향 벡터, $\textrm{RGB}(\cdot)$는 SH를 RGB로 변환하는 함수)

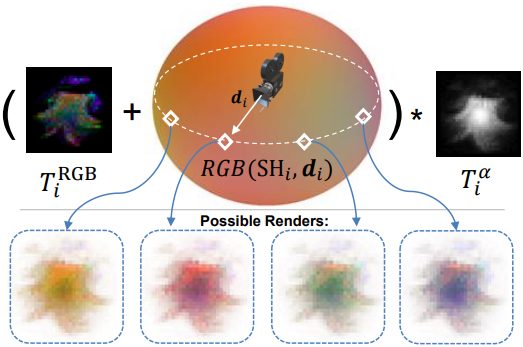
이렇게 하면 텍스처가 적용된 평면에 대한 view-dependent한 조명 효과를 처리할 수 있다. 또한, 이 방식은 \(T_i^\textrm{RGB}\)가 sparse한 구조를 가질 수 있게 하여, 저장 효율이 더 높다. Billboard의 최종 parametrization은 다음과 같다.

\[\begin{equation} \{\mu_i, s_i, r_i, \textrm{SH}_i, T_i^\textrm{RGB}, T_i^\alpha \} \end{equation}\]

Billboard 분할에서 alpha map을 사용하는 것은 제한된 수의 billboard에 대해서도 상세한 장면 표현을 가능하게 하기 때문에 정확한 메쉬 추출에 매우 중요하다. 메쉬는 학습 뷰에 해당하는 depth map을 렌더링하고 TSDF를 사용하여 추출한다.

2. Training

장면의 billboard 표현을 학습하기 위해 SfM을 사용하여 얻은 sparse 포인트 클라우드로 초기화한다. 선택적으로, Fibonacci 알고리즘을 사용하여 외접 구에 균등하게 분포된 10,000개의 점을 추가하여 하늘과 멀리 있는 물체를 표현한다.

Photometric losses

Photometric loss를 활용하여 billboard 표현을 학습시킨다. 따라서 장면을 표현하는 방법을 학습시키기 위해서는 이미지 세트만 필요하다.

\[\begin{equation} \mathcal{L}_\textrm{image} = (1 - \lambda_\textrm{SSIM}) \mathcal{L}_1 + \lambda_\textrm{SSIM} \mathcal{L}_\textrm{SSIM} \end{equation}\]

Regularizations

파라미터수의 수가 많기 때문에 텍스처는 학습 이미지에 overfitting되는 경향이 있으며, 이로 인해 새로운 뷰에 대한 렌더링 출력에 노이즈가 발생한다. 이 문제를 해결하기 위해, 렌더링에 미치는 영향이 적은 billboard, 즉 픽셀에 영향을 거의 미치지 않는 작거나 먼 billboard를 Gaussian 분포 투명도를 갖도록 푸시하는 간단하면서도 효율적인 정규화를 사용한다.

먼저, 렌더링된 이미지에 미치는 영향 $I_i$를 기반으로 모든 $N$개의 billboard에 대해 텍스처별 visibility 가중치 $w_i$를 정의한다. $i$번째 billboard에 대한 영향은 렌더링된 픽셀 \(\mathcal{R}_i\)에 해당하는 알파 블렌딩 값의 합으로 정의한다.

\[\begin{aligned} I_i &= \sum_{x \in \mathcal{R}_i} \left( T_i^\alpha [\textbf{u} (x)] \cdot \prod_{j=1}^{K_x} \left( 1 - T_j^\alpha [\textbf{u} (x)] \right) \right) \\ w_i &= \begin{cases} \sigma - \textrm{min}(I_i, \sigma), & \textrm{if} \; I_i > 0 \\ 0, & \textrm{otherwise} \end{cases} \end{aligned}\]

알파 블렌딩 값은 2DGS와 유사하게 계산되며, 픽셀 $x$에서 $K_x$개의 평면이 겹치는 것을 고려한다. 최대 영향 threshold $\sigma = 500$을 사용하여 명확하게 보이는 billboard만 정규화한다. $I_i \le 0$인 billboard를 무시함으로써 프레임에서 보이지 않는 부분은 정규화하지 않고, 과소 표현된 영역에서 과도한 정규화를 방지한다. 제안된 기준은 hitting frustum만 고려하고 겹침을 무시하기 때문에 2DGS처럼 projected radii를 사용하는 기준보다 더 효율적이다.

RGB 텍스처를 0에 가깝게, 그리고 alpha map을 visibility 가중치 $w_i$를 기반으로 Gaussian 분포 $\mathcal{G}$에 가깝게 밀어내기 위한 정규화 항은 다음과 같이 정의된다.

\[\begin{aligned} \mathcal{L}_\textrm{RGB} &= \frac{1}{N} \sum_{i=0}^N w_i \| T_i^\textrm{RGB} \| \\ \mathcal{L}_\alpha &= \frac{1}{N} \sum_{i=0}^N w_i \| T_i^\alpha - \mathcal{G} \| \\ \mathcal{L}_\textrm{texture} &= \lambda_\textrm{RGB} \mathcal{L}_\textrm{RGB} + \lambda_\alpha \mathcal{L}_\alpha \end{aligned}\]

학습을 위한 최종 loss는 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{image} + \mathcal{L}_\textrm{texture} \end{equation}\]

3. Adaptive density control

대부분의 3DGS 기반 방법은 adaptive density control을 사용하여 Gaussian의 개수를 조정한다. 3DGS-MCMC에서는 densification을 Markov Chain Monte Carlo (MCMC) 샘플링으로 재구성하는 대안적인 접근 방식을 제안하였다. MCMC는 학습 과정에 노이즈를 도입하고 분할 및 복제를 deterministic state transition으로 대체한다.

저자들은 MCMC 샘플링 기법을 채택하고 수정하였다. 샘플링 단계에서 MCMC는 Gaussian을 복제하고, \(\Sigma_i\)와 $o_i$를 조정하여 렌더링 출력 상태를 유지한다.

\[\begin{equation} o_{1, \ldots, N}^\textrm{new} = 1 - \sqrt[N]{1 - o_N^\textrm{old}} \\ \Sigma_{1, \ldots, N}^\textrm{new} = (o_N^\textrm{old})^2 \left( \sum_{i=1}^N \sum_{k=0}^{i-1} \left( \binom{i-1}{k} \frac{(-1)^k (o_N^\textrm{new})^{k+1}}{\sqrt{k+1}} \right) \right)^{-2} \end{equation}\]

이러한 조정은 Gaussian에는 잘 적용되지만, scale 조정은 임의 형태의 primitive에는 적합하지 않으며 렌더링 상태 보존을 위반한다. 대신, \(T_i^\alpha\)만 조정하여 광선을 따라 전체적인 투명도를 유지한다. 이는 평면의 모든 점에서 투명도를 제어하기 때문에 추가적인 scale 조정이 필요하지 않기 때문이다.

\[\begin{equation} T_{1, \ldots, N}^\alpha = 1 - \sqrt[N]{1 - T_N^\alpha} \end{equation}\]

MCMC는 불투명도 $o_i$를 미리 정의된 threshold $\gamma = 5 \times 10^{-3}$와 비교하여 dead Gaussian을 결정하지만, 본 논문에서는 alpha map의 평균값을 비교한다.

\[\begin{equation} \bar{T_i^\alpha} < \gamma \end{equation}\]

4. Texture compression

텍스처가 적용된 splat을 사용하면 효율적으로 저장하는 데 새로운 어려움이 발생한다. 각 지점에 대해 $S_T \times S_T$ 크기의 텍스처 2개를 사용하며, 투명도 채널 하나와 색상 채널 세 개를 사용한다. 텍스처가 4바이트 부동 소수점 값으로 저장된다는 점을 고려하면, 각 텍스처를 저장하기 위해 $(16S_T^2)$ byte의 메모리가 필요하다.

저장 비용을 줄이기 위해 먼저 텍스처 파라미터의 quantization을 적용한다. 정규화된 $[0, 1]$ 범위 내 텍스처 값을 $\epsilon$이라 하면, BBSplat을 저장하기 위해 $\hat{\epsilon} = \lfloor \epsilon \times 255 \rceil$로 rescaling하여 텍스처 값을 quantize한다 ($\lfloor \cdot \rceil$은 반올림 연산). 텍스처를 로드할 때는 dequantization을 위해 $\epsilon = \hat{\epsilon} / 255$의 역연산을 적용한다. 이렇게 하면 각 texel 값 $\hat{\epsilon}$을 1 byte로 저장할 수 있어 저장 비용을 4배 줄일 수 있다.

최종 색상 표현은 SH와 텍스처 샘플링 offset을 사용하여 계산된 색상의 합으로, 저장 비용을 추가로 절감할 수 있다. 정규화 항 \(\mathcal{L}_\textrm{texture}\)를 사용하면 $T^\textrm{RGB}$ 값을 더 sparse하게 만들고 $T^\alpha$를 Gaussian 분포 $\mathcal{G}$에 더 가깝게 만들 수 있다. $T^\alpha$에서 Gaussian 패턴 $\mathcal{G}$를 빼서 $T^\alpha$의 sparsity를 높이고 텍스처에 더 많은 0 값을 포함시킨다. 텍스처의 sparsity 덕분에 효율적인 dictionary 기반 압축 방법(ex. ZIP)을 사용하여 저장 비용을 더욱 절감할 수 있다. 텍스처 압축 파이프라인을 통해 메모리 소비를 평균 약 7배 줄일 수 있다.

Experiments

• 구현 디테일
  • $S_T = 16$
  • \(\lambda_\textrm{SSIM} = 0.2\), \(\lambda_\textrm{RGB} = \lambda_\alpha = 10^{-4}\)
  • $T^\textrm{RGB}$는 0으로, $T^\alpha$는 2D Gaussian으로 초기화하고, 처음 500 iteration 동안 고정
  • Densification은 500 iteration에서 25,000 iteration까지 적용
  • 30,000 iteration 학습 후, 추가 2,000 iteration동안 SH만 fine-tuning
  • learning rate: $T^\textrm{RGB}$는 0.0025, $T^\alpha$는 0.001, SH는 0.005

1. Results and Evaluation

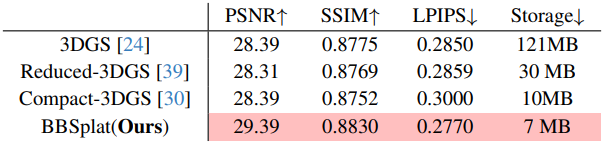
다음은 각 방법의 최고 렌더링 품질을 비교한 결과이다.

다음은 고정된 저장 공간에 대한 렌더링 품질을 비교한 결과이다.

다음은 3DGS를 위한 압축 방법들과 비교한 결과이다.

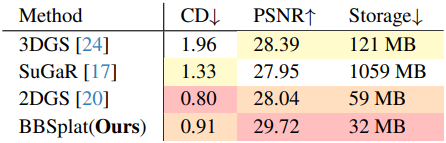
다음은 DTU 데이터셋에서 Chamfer distance를 비교한 결과이다.

다음은 rasterization 중에 ray-tracing을 적용한 예시이다.

2. Ablation study

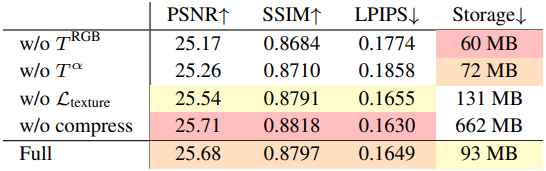
다음은 Tanks&Temples 데이터셋에서의 ablation study 결과이다.