[논문리뷰] Guiding a Diffusion Model with a Bad Version of Itself
NeurIPS 2024 (Oral). [Paper] [Github]
Tero Karras, Miika Aittala, Tuomas Kynkäänniemi, Jaakko Lehtinen, Timo Aila, Samuli Laine
NVIDIA | Aalto University
4 Jun 2024
Introduction
Diffusion model의 학습 목표는 전체 데이터 분포를 포괄하는 것이다. 이는 확률이 낮은 영역에서 문제를 일으킨다. 모델은 이를 표현하지 못한다는 이유로 엄청난 처벌을 받지만, 이에 상응하는 좋은 이미지를 생성하는 데 필요한 데이터가 충분하지 않습니다. Classifier-free guidance (CFG)는 잘 학습된 높은 확률 영역에 생성을 집중하는 표준 방법이 되었다. Conditional과 unconditional 모두에서 작동하도록 denoiser를 학습시킴으로써 샘플링 프로세스는 unconditional한 결과에서 벗어날 수 있으며, 사실상 unconditional은 피해야 할 결과를 지정한다. 이는 더 나은 프롬프트 정렬과 향상된 이미지 품질을 가져오는데, 전자의 효과는 CFG가 확률 밀도의 조건부 부분을 암시적으로 높이기 때문이다.
그러나 CFG는 일반적인 방법으로서의 사용을 제한하는 단점이 있다.
- Conditional 생성에만 적용할 수 있다. Guidance 신호는 conditional denoising 결과와 unconditional denoising 결과의 차이에 기반하기 때문이다.
- Unconditional denoiser와 conditional denoiser는 다른 task를 해결하도록 학습되기 때문에 샘플링 궤적이 원하는 조건부 분포를 초과할 수 있으며, 이로 인해 이미지 구성이 왜곡되고 종종 지나치게 단순화된다.
- 프롬프트 정렬 및 품질 개선 효과는 별도로 제어할 수 없으며, 정확히 어떻게 서로 관련되어 있는지는 불분명하다.
본 논문에서는 CFG가 이미지 품질을 개선하는 이유에 대한 새로운 통찰력을 제공하고 이 효과를 autoguidance라고 부르는 새로운 방법으로 분리할 수 있는 방법을 보여주었다. Autoguidance는 주요 모델 자체의 열등한 버전을 guidance model로 사용하고 조건은 변경하지 않기 때문에 task 불일치 문제가 발생하지 않는다. 이 guidance model은 모델 용량이나 학습 시간 등을 간단히 제한하여 얻을 수 있다.
Autoguidance는 unconditional한 합성에 대한 guidance를 가능하게 하며, ImageNet-512와 ImageNet-64 생성에서 새로운 기록을 세웠다.
Classifier-free guidance
복잡한 데이터셋의 경우, 생성된 이미지는 유한한 용량의 네트워크에서 발생한 근사 오차로 인해 종종 학습 이미지의 선명도를 재현하지 못한다. 널리 사용되는 기법인 classifier-free guidance (CFG)는 샘플을 해당 클래스 레이블의 더 높은 likelihood로 밀어내어 다양성을 희생하는 대신, 네트워크가 더 잘 처리할 수 있는 더 정형화된 이미지를 생성하도록 한다.
Diffusion model의 guidance에는 두 개의 denoiser $D_0 (\textbf{x}; \sigma, \textbf{c})$와 $D_1 (\textbf{x}; \sigma, \textbf{c})$이 포함된다. Guidance 효과는 두 denoising 결과 사이를 $w$로 외삽하여 얻을 수 있다.
\[\begin{equation} D_w (\textbf{x}; \sigma, \textbf{c}) = w D_1 (\textbf{x}; \sigma, \textbf{c}) + (1 - w) D_0 (\textbf{x}; \sigma, \textbf{c}) \end{equation}\]$w = 0$ 또는 $w = 1$로 설정하면 각각 $D_0$와 $D_1$의 출력이 복구되고, $w > 1$을 선택하면 $D_1$의 출력이 과도하게 강조된다. Denoiser와 score의 동등성을 생각하면 다음과 같이 쓸 수 있다.
\[\begin{equation} D_w (\textbf{x}; \sigma, \textbf{c}) \approx \textbf{x} + \sigma^2 \nabla_\textbf{x} \log \underbrace{\left( p_0 (\textbf{x} \vert \textbf{c}; \sigma) \left[ \frac{p_1 (\textbf{x} \vert \textbf{c}; \sigma)}{p_0 (\textbf{x} \vert \textbf{c}; \sigma)} \right]^w \right)}_{\propto \; p_w (\textbf{x} \vert \textbf{c}; \sigma)} \end{equation}\]따라서 guidance는 \(p_w (\textbf{x} \vert \textbf{c}; \sigma)\)의 score에 접근할 수 있게 해준다. 이 score는 다음과 같이 쓸 수 있다.
\[\begin{equation} \nabla_\textbf{x} \log p_w (\textbf{x} \vert \textbf{c}; \sigma) = \nabla_\textbf{x} \log p_1 (\textbf{x} \vert \textbf{c}; \sigma) + (w - 1) \nabla_\textbf{x} \log \frac{p_1 (\textbf{x} \vert \textbf{c}; \sigma)}{p_0 (\textbf{x} \vert \textbf{c}; \sigma)} \end{equation}\]CFG에서는 $\textbf{c}$에 대해 marginalize된 분포 $p(\textbf{x}; \sigma)$의 noise를 제거하기 위해 unconditional denoiser $D_\theta (\textbf{x}; \sigma)$를 학습시키고 이를 $D_0$로 사용한다. 실제로는 빈 컨디셔닝 레이블을 사용할 수 있는 동일한 네트워크 $D_\theta$를 사용하며,
\[\begin{equation} D_0 := D_\theta (\textbf{x}; \sigma, \varnothing), \quad D_1 := D_\theta (\textbf{x}; \sigma, \textbf{c}) \end{equation}\]로 세팅한다. Bayes’ rule에 따라 guidance가 적용된 score 벡터는
\[\begin{aligned} \nabla_\textbf{x} \log p_w (\textbf{x} \vert \textbf{c}; \sigma) &= \nabla_\textbf{x} \log p (\textbf{x} \vert \textbf{c}; \sigma) + (w - 1) \nabla_\textbf{x} \log \frac{p (\textbf{x} \vert \textbf{c}; \sigma)}{p (\textbf{x}; \sigma)} \\ &= \nabla_\textbf{x} \log p (\textbf{x} \vert \textbf{c}; \sigma) + (w - 1) \nabla_\textbf{x} \log \frac{p (\textbf{c} \vert \textbf{x}; \sigma)}{p (\textbf{c}; \sigma)} \\ &= \nabla_\textbf{x} \log p (\textbf{x} \vert \textbf{c}; \sigma) + (w - 1) \nabla_\textbf{x} \log p (\textbf{c} \vert \textbf{x}; \sigma) - (w - 1) \nabla_\textbf{x} \log p (\textbf{c}; \sigma) \\ &= \nabla_\textbf{x} \log p (\textbf{x} \vert \textbf{c}; \sigma) + (w - 1) \nabla_\textbf{x} \log p (\textbf{c} \vert \textbf{x}; \sigma) \end{aligned}\]가 된다. 따라서 샘플링하는 동안 이미지가 클래스 $\textbf{c}$와 더 강하게 일치하도록 가이드한다.
Why does CFG improve image quality?
저자들은 CFG가 이미지 품질을 개선하는 메커니즘을 식별하는 것으로 시작하였다.
- 가이드되지 않은 diffusion model이 종종 만족스럽지 못한 이미지를 생성하는 이유는 무엇인가?
- CFG는 이 문제를 어떻게 해결하는가?
저자들은 작은 denoiser가 합성 데이터셋에서 조건부 diffusion을 수행하도록 학습된 2D toy example에서 실험을 진행하였다. 이 데이터셋은 낮은 local dimensionality와 noise가 제거됨에 따라 계층적인 로컬 디테일이 나타내도록 설계되었다. 이 두 가지 속성은 모두 사실적인 이미지의 실제 manifold에서 예상할 수 있는 속성이다.
실험 결과는 아래와 같다. (c)에서 CFG weight은 $w = 4$를 적용하였다.
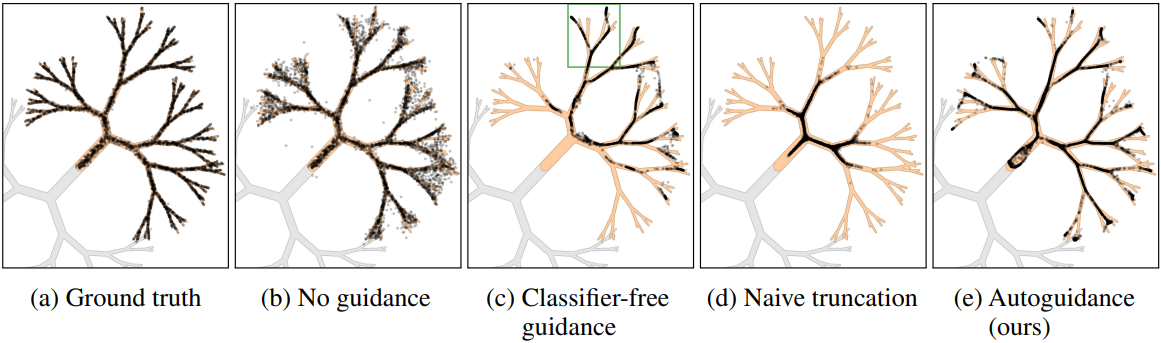
다음은 CFG를 적용한 (c)의 초록색 박스 영역을 확대한 것이다.
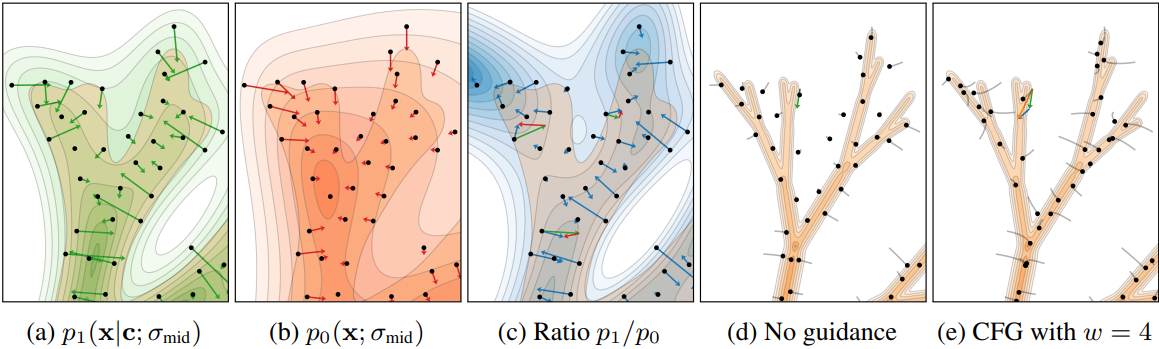
Score matching으로 인해 outlier가 발생한다.
기본 분포에서 직접 샘플링하는 것과 비교했을 때, 가이드되지 않은 diffusion은 대부분 분포 밖에서 매우 확률이 낮은 샘플을 대량으로 생성한다. 이미지 생성에서 이는 비현실적이고 망가진 이미지에 해당한다.
저자들은 이 outlier가 score network의 제한된 역량과 score matching 목적 함수의 결합에서 비롯된다고 주장하였다. Maximum likelihood estimation (MLE)는 모델이 모든 학습 샘플을 포함하려고 시도한다는 의미에서 데이터 분포를 보수적으로 fitting한다. 이는 모델이 모든 학습 샘플의 likelihood를 심각하게 과소평가할 경우 KL divergence가 큰 페널티를 주기 때문이다. Score matching은 일반적으로 MLE와 같지 않지만, 둘은 밀접한 관련이 있으며 광범위하게 유사한 동작을 보인다.
두 번째 그림의 (a)와 (b)는 서로 다른 용량의 두 모델에 대한 toy example에서 학습된 score field와 확률 밀도를 보여준다. 더 강한 모델은 데이터를 더 단단히 포괄하는 반면, 더 약한 모델의 확률 밀도는 더 퍼져 있다.
이미지 생성의 관점에서 전체 학습 데이터를 커버하려는 경향은 문제가 된다. 모델은 데이터 분포의 극단에서 이상하고 낮은 확률의 이미지를 생성하게 되는데, 이는 정확하게 학습되지 않고 높은 loss를 피하기 위해 포함된다. 게다가, 학습하는 동안 네트워크는 입력으로 실제 이미지의 noisy한 버전만 보았고, 샘플링하는 동안 더 높은 noise level에서 전달되는 낮은 확률의 샘플을 처리할 준비가 되어 있지 않을 수 있다.
CFG는 outlier를 제거한다.
CFG를 적용한 경우, 예상대로 샘플은 클래스 경계를 피하고 (즉, 회색 영역 근처에 샘플이 없음) 분포의 전체 분기가 제거된다. 또한 샘플이 manifold의 핵심 쪽으로 당겨지고 낮은 확률의 중간 영역에서 멀어지는 현상을 관찰할 수 있다. 이를 통해 확률이 낮은 outlier 샘플을 제거하여 이미지 품질이 향상된다. 그러나 클래스 likelihood의 단순한 증가만으로는 이러한 농도 증가를 설명할 수 없다.
저자들은 이 현상이 conditional denoiser와 unconditional denoiser 사이의 품질 차이에서 비롯된다고 주장하였다. Denoiser $D_0$는 모든 클래스에서 한 번에 생성해야 하는 더 어려운 task에 직면하는 반면, D1은 특정 샘플에 대해 하나의 클래스에 집중할 수 있다. 따라서 네트워크 $D_0$는 데이터에 더 좋지 못한 fitting을 얻는다.
CFG는 샘플이 클래스 $\textbf{c}$에서 나올 likelihood를 높일 뿐만 아니라 더 높은 품질의 분포에서 나올 likelihood도 높인다. Guidance는 샘플을 더 높은 $\log (p_1 / p_0)$ 값으로 끌어당기는 추가적인 힘으로 작용한다. 두 번째 그림의 (c)에서 볼 수 있듯이, 분모 $p_0$가 더 퍼진 분포를 나타내기 때문에 manifold와의 거리에 따라 비율이 일반적으로 감소하고 분자 $p_1$보다 더 느리게 감소하는 것을 알 수 있다. 결과적으로 기울기는 데이터 manifold의 안쪽을 가리킨다.
Discussion
두 모델이 비슷한 위치에서 데이터에 적절히 fitting하지 못하는 문제를 겪을 수 있지만, 그 정도는 서로 다르다. Denoiser의 예측은 이러한 영역에서 더욱 불일치한다. 따라서 CFG는 샘플이 underfitting할 가능성이 높은 시점을 식별하고 더 나은 샘플의 일반적인 방향으로 밀어내는 적응적 truncation의 한 형태로 볼 수 있다. Truncation은 GT보다 좁은 분포를 생성하지만 실제로는 이미지에 부정적인 영향을 미치지 않는다.
이와 대조적으로, GAN의 truncation 트릭이나 언어 모델의 temperature 낮추기와 비슷하게 truncation을 하려고 시도하면, score 벡터를 $w > 1$의 factor로 균일하게 길게 하여 smoothing을 상쇄할 것이다. 이는 첫 번째 그림의 (d)에서 설명되는데, 샘플은 실제로 높은 확률의 영역에 집중되어 있지만 바깥쪽 가지가 비어 있다. 실제로 이런 방식으로 생성된 이미지는 다양성이 적고, 지나치게 단순화된 디테일과 단조로운 텍스처를 보이는 경향이 있다.
Method
저자들은 동일한 task, 컨디셔닝, 데이터 분포에 대해 학습되었지만 낮은 용량이나 적은 학습 등으로 어려움을 겪는 저품질 모델 $D_0$로 고품질 모델 $D_1$을 직접 가이드하여 이미지 품질 개선 효과를 분리하는 것을 제안하였다. 모델이 스스로의 열등한 버전으로 가이드되기 때문에 이 절차를 autoguidance라고 부른다.
2D toy example에서 autoguidance는 놀라울 정도로 잘 작동한다. 첫 번째 그림의 (e)는 더 적은 학습으로 더 작은 $D_0$를 사용하는 효과를 보여준다. 의도한 바와 같이, 샘플은 일부를 삭제하지 않고 분포에 가깝게 당겨진다.
제한된 모델 용량에서 score matching은 데이터 분포의 낮은 확률, 즉 비현실적이고 학습이 부족한 영역을 과도하게 강조하는 경향이 있다. 문제가 정확히 어디에 어떻게 나타나는지는 네트워크 아키텍처, 데이터셋, 학습 디테일 등과 같은 다양한 요인에 따라 달라지며, 사전에 특정 문제를 식별하고 이에 맞추어 학습시킬 수는 없다.
그러나 동일한 모델의 약한 버전은 동일한 영역에서 광범위하게 유사한 오차를 만들면서 더 강한 오차를 만들 것으로 예상할 수 있다. Autoguidance는 약한 모델의 예측과의 차이를 측정하고 이를 부스트하여 더 강한 모델이 만든 오차를 식별하고 줄이려고 한다. 두 모델이 일치할 때는 중요하지 않지만, 일치하지 않을 때 차이는 더 나은 샘플을 향한 일반적인 방향을 나타낸다.
따라서 두 모델이 서로 동일한 어려움을 겪는다면 autoguidance가 작동할 것으로 기대할 수 있다. 모든 $D_1$는 어느 정도의 어려움을 겪을 것으로 예상되므로 이러한 측면을 더욱 악화시키도록 $D_0$를 선택하는 것이 합리적이다.
실제로, 별도로 학습되거나 다른 iteration 수로 학습된 모델은 fitting 정확도뿐만 아니라, 가중치의 랜덤 초기화나 학습 데이터 셔플링 등의 측면에서도 차이가 있다. 효과적인 guidance를 위해서는 품질 차이가 충분히 커야 하며, 그래야만 확률 밀도의 체계적인 확장이 이러한 랜덤 효과를 압도할 수 있다.
Degradation에 대한 연구
저자들은 두 모델이 동일한 종류의 어려움을 겪어야 한다는 가설을 검증하기 위해, 잘 학습된 이미지 diffusion model을 의도적으로 손상시켜 통제된 실험을 수행하였다. Base model에 다양한 정도의 손상을 적용하여 main model $D_1$과 guiding model $D_0$를 만든다. 이 구성을 통해 $D_1$와 $D_0$에 적용된 다양한 손상 조합의 FID 효과를 측정할 때 손상되지 않은 base model을 기준으로 사용할 수 있다.
- Base model: ImageNet-512에서 학습된 EDM2-S (FID 2.56).
- Dropout: Base model에 dropout을 각각 5%와 10% 적용한 $D_1$과 $D_0$를 구성 (각각 FID는 4.98, 15.00). Autoguidance를 적용한 후, FID 2.55를 달성 ($w$ = 2.25).
- Input noise: Base model을 수정하여 입력 이미지에 noise를 추가하여 noise level을 각각 10%와 20% 증가시켜 $D_1$과 $D_0$를 구성 (각각 FID는 3.96, 9.73). Autoguidance를 적용한 후, FID 2.56을 달성 ($w$ = 2.00).
- Mismatched degradations: $D_1$을 dropout으로 손상시키고 $D_0$를 입력 noise로 손상시키거나 그 반대로 손상시키는 경우, autoguidance는 결과를 전혀 개선하지 못함. $w = 1$로 설정하여 $D_1$만 사용하였을 때 가장 좋은 FID를 얻음.
Results
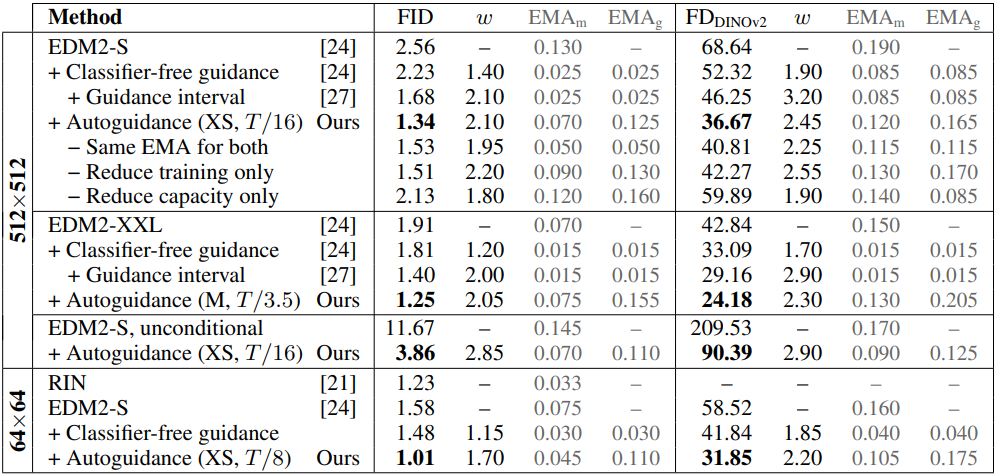
다음은 ImageNet-512과 ImageNet-64에서의 결과를 비교한 표이다. Autoguidance의 파라미터는 guiding model $D_0$의 모델 용량과 학습량을 나타낸다 ($T$는 메인 모델의 학습량). EMAm과 EMAg는 각각 main model과 guiding model의 사후 EMA 기법에 대한 길이 파라미터이다.
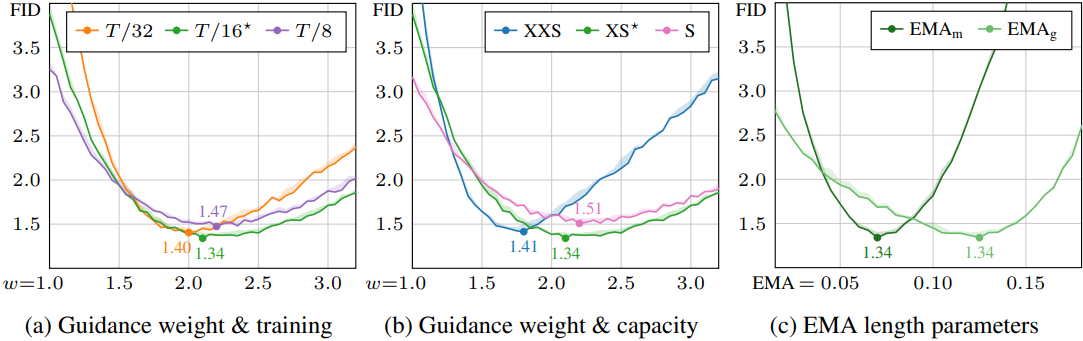
다음은 autoguidance 파라미터에 대한 효과를 나타낸 그래프이다. (EDM2-S, ImageNet-512)
다음은 CFG와 생성 결과를 비교한 것이다. (EDM2-S, ImageNet-512)

다음은 DeepFloyd IF에 대한 결과이다. (프롬프트: “A blue jay standing on a large basket of rainbow macarons”)
