[논문리뷰] AR-Diffusion: Auto-Regressive Diffusion Model for Text Generation
NeurIPS 2023. [Paper] [Github]
Tong Wu, Zhihao Fan, Xiao Liu, Yeyun Gong, Yelong Shen, Jian Jiao, Hai-Tao Zheng, Juntao Li, Zhongyu Wei, Jian Guo, Nan Duan, Weizhu Chen
Tsinghua University | Fudan University | Microsoft Research Asia | Microsoft | Soochow University | IDEA Research
16 May 2023
Introduction
텍스트 생성은 자연어 처리 (NLP) 분야의 기본 task이다. GPT-4, LLaMA, Alpaca와 같은 사전 학습된 언어 모델은 유창하고 사람과 같은 텍스트 콘텐츠를 생성하는 능력으로 상당한 주목을 받았다. 이러한 모델은 autoregressive (AR) transformer 디코더를 활용하여 생성된 토큰을 왼쪽에서 오른쪽으로 순차적으로 하나씩 내보낸다. AR 모델은 위치 의존성의 힘을 활용하여 생성된 텍스트에서 자연스러움, 일관성, 인간 언어 규칙 준수를 향상할 수 있다.
최근 연구는 이미지 생성에서 diffusion model의 놀라운 성능을 보여주었고, 연구자들은 diffusion을 텍스트 생성으로 확장하도록 동기를 부여했다. Timestep을 도입함으로써 이러한 방법은 원래 토큰과 Gaussian noise 사이의 보간을 점진적으로 조절한 다음 텍스트 생성을 위해 반복적으로 noise를 제거한다. 각 timestep에서 diffusion 기반 텍스트 생성기는 Non-Auto-Regression (NAR)에 따라 모든 토큰을 동시에 예측하므로 AR에 비해 디코딩 속도가 빠르다. 그러나 NAR의 단점, 즉 토큰 간 위치 의존성 희생과 생성 성능 저하도 상속한다.
포괄적인 분석을 수행하기 위해 다양한 위치에 위치한 토큰 $f(\cdot)$의 diffusion timestep을 추적하는 2차원 좌표계를 도입한다.
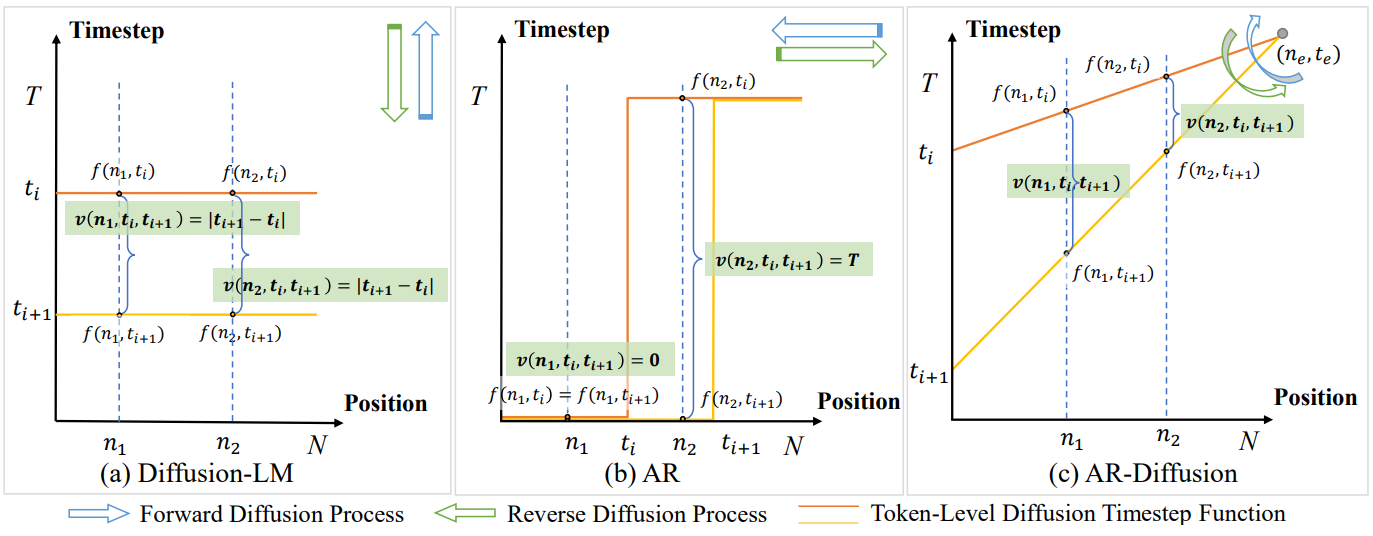
위 그림과 같이 시스템은 토큰 위치 $n \in [1, N]$을 수평축에 할당하고 확산 시간 단계 $t \in [0,T]$를 수직축에 할당한다. 기존의 diffusion 기반 텍스트 생성 모델이 뒤따르는 Diffusion-LM은 (a)에 나와 있다. 모든 토큰에 균일한 timestep $t$를 할당한다. 대조적으로, (b)에 묘사된 AR 모델의 토큰은 생성 step ($t_i$) 내에서 뚜렷한 timestep을 나타낸다. 예를 들어 위치 $n_1$에서 이미 디코딩된 토큰은 timestep이 0인 반면 위치 $n_2$에서 디코딩될 토큰은 timestep이 $T$다. 이 접근 방식은 순차적 의존성을 효과적으로 캡처한다. 본 논문은 이러한 관찰에 동기를 부여하여 토큰 위치의 격차와 순차적인 토큰 식별 원리에 대한 autoregressive diffusion 방법인 AR-Diffusion을 소개한다.
AR-Diffusion에서는 문장 레벨의 diffusion과 토큰 레벨의 diffusion을 모두 포함하는 multi-level diffusion 전략을 제안한다. 문장 레벨 timestep $t$를 무작위로 선택하고 각 토큰에 대해 위치에 민감한 토큰 레벨 timestep $f(n, t)$를 결정하여 동적 이동 속도 $v(\cdot)$를 할당한다. 이를 통해 문장의 왼쪽에 있는 토큰은 랜덤 Gaussian noise에서 토큰 임베딩으로 더 빠르게 이동하는 반면, 문장의 오른쪽에 있는 토큰은 이전에 denoise된 토큰의 정보를 더 잘 활용하기 위해 더 느린 움직임을 경험한다. Inference 중에 Diffusion-LM, SeqDiffSeq, GENIE에 필요한 상당한 수의 inference 단계 (ex. 2000)를 줄이고 프로세스를 가속화하기 위해 multi-level diffusion 전략과 협력하는 skipping 메커니즘을 도입한다.
텍스트 요약, 기계 번역, 상식 생성과 같은 다양한 텍스트 생성 task에 대한 실험 결과는 AR-Diffusion이 품질과 다양성 측면에서 AR 방법을 포함한 기존 텍스트 diffusion model을 능가한다는 것을 지속적으로 입증한다. 또한 AR-Diffusion은 우수한 성능을 유지하면서 디코딩하는 동안 더 적은 리소스를 필요로 한다. 기계 번역에서 SeqDiffSeq보다 100배 빠르고 텍스트 요약에서 GENIE보다 600배 빠르며 비슷한 결과를 제공한다. 또한 디코딩이 두 step으로 제한되는 어려운 시나리오에서도 유망한 결과를 보여준다.
Methodology
1. Multi-Level Diffusion
일반적인 diffusion process에서 텍스트 시퀀스의 모든 토큰은 동일한 diffusion timestep을 갖는다. 언어의 순차적 특성을 활용하기 위해 forward 및 reverse pass 중에 토큰이 서로 다른 timestep을 갖도록 한다. 이를 위해 문장 레벨 diffusion과 토큰 레벨 diffusion을 모두 포함하는 multi-level diffusion 전략을 제안한다.
먼저 문장 레벨에서 Diffusion-LM을 따라 timestep $t$를 무작위로 선택한다. 둘째, 토큰 레벨에서 현재 토큰에 대한 diffusion timestep을 규제하기 위해 문장 레벨 timestep을 기반으로 위치 정보 $n \in [1, N]$을 통합한다. 절차는 다음과 같다.
\[\begin{equation} z_t = (z_{f(1, t)}^1, z_{f(2, t)}^2, \cdots, z_{f(N, t)}^N) \end{equation}\]여기서 $N$은 주어진 타겟 문장 길이이고, $z_t$는 timestep $t$에서의 문장 표현이고, $z_{f(n,t)}^n$은 문장 레벨 timestep $t$에서 $n$번째 토큰에 대한 latent 표현이며, $f(n, t)$는 토큰 위치 $n$과 문장 레벨 timestep $t$에 의해 결정되는 토큰 레벨 timestep을 나타내는 토큰 레벨 timestep 함수이다.
움직임의 특성을 보다 심도 있게 설명하기 위해 움직임의 속도를 다음과 같이 정의한다.
\[\begin{equation} v(n, t_i, t_{i+1}) = f(n, t_{i+1}) - f(n, t_i) \end{equation}\]여기서 $t_i$와 $t_{i+1}$은 시작 및 끝 문장 레벨 timestep이다. Diffusion-LM의 토큰은 동일한 이동 속도를 공유하는 반면 AR의 토큰은 서로 다른 속도를 가진다.
2. Token-Level Diffusion with Dynamic Movement Speed
본 논문은 이동 속도를 기반으로 diffusion에서 AR을 활용하기 위해 토큰 레벨의 timestep 함수 $f(n, t)$를 설계하기 위한 기본 원칙인 동적 이동 속도를 제안한다. 구체적으로 문장의 왼쪽에 있는 요소는 랜덤 Gaussian noise에서 토큰 임베딩까지 더 빠른 이동 속도로 이동하고, 오른쪽에 있는 요소는 더 낮은 이동 속도로 이동하므로 나중 문장 레벨 timestep에서 생성되어 이전에 생성된 토큰의 정보를 보다 효과적으로 활용할 수 있다.

원칙의 guidance에 따라 선형 함수를 사용하여 토큰 레벨 diffusion 전략을 개발한다. 절차는 Algorithm 1에 설명되어 있으며 여기서 $\textrm{clip} (x, \textrm{min}, \textrm{max})$ 함수는 $x$의 모든 요소를 $[\textrm{min}, \textrm{max}]$ 범위로 고정한다. 구체적으로 diffusion의 forward process에서 시작점은 가로축을 따라 왼쪽으로 $(N, 0)$에서 $(0, 0)$으로 이동한 다음 세로축을 따라 위로 $(0, T)$로 이동한다. 따라서 문장 레벨 timestep의 전체 범위는 $[0, N + T]$로 확장된다.
Reverse process에서 multi-level diffusion은 다음 공식을 따른다.
\[\begin{equation} g_\theta (z_t, t; x) = g_\theta ((z_{f(1,t)}^1, f(1,t)), (z_{f(2,t)}^2, f(2,t)), \cdots, (z_{f(N,t)}^N, f(N,t)); x) \end{equation}\]여기서 $g_\theta (z_{f(n,t)}^n, f(n, t); x)$는 $n$번째 요소를 나타낸다.
3. Inference with Skipping
일반적으로 생성 프로세스는 $T + N$에서 0까지 모든 문장 레벨 timestep을 거쳐야 한다. 디코딩 시간을 줄이기 위해 timestep의 부분 집합을 통과할 수 있는 skipping 메커니즘을 도입한다.

Inference를 위한 알고리즘은 Algorithm 2와 같다.
$z_{t_{i+1}}$의 조건부 분포는 $p_\theta (z_{t_{i+1}} \vert z_{t_i}; x)$에 의해 추론된 다음 서로 다른 위치에 있는 요소의 독립적인 forward process로 인해 위치별로 분해한다.
Experiments
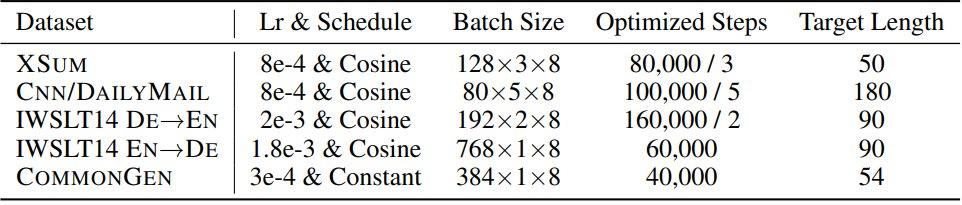
학습 파라미터는 아래 표와 같다. $N_{gc}$를 gradient accumulation 수라고 하면, Batch Size는 mini batch size $\times N_{gc} \times$ GPU 수이며, Optimized Steps는 전체 step 수 / $N_{gc}$이다.
1. Main Results
Text Summarization
다음은 XSUM test set에서의 결과이다.

다음은 Cnn/DailyMail test set에서의 결과이다.
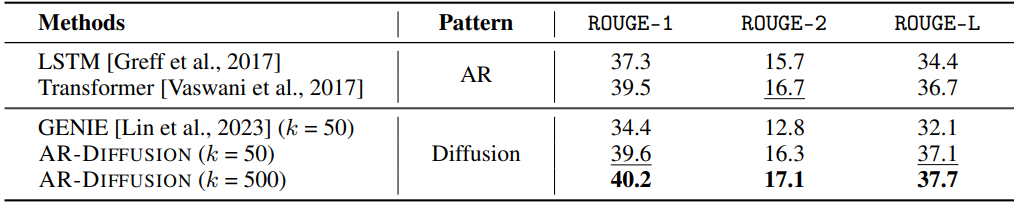
Machine Translation
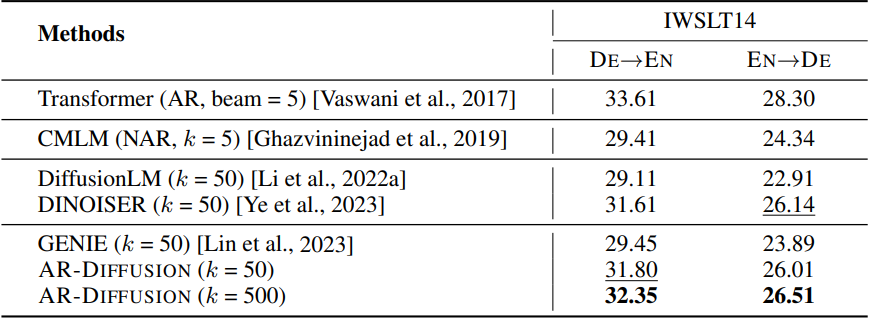
다음은 IWSLT14 DE $\rightarrow$ EN test set에서 SeqDiffSeq의 세팅을 따른 결과이다.
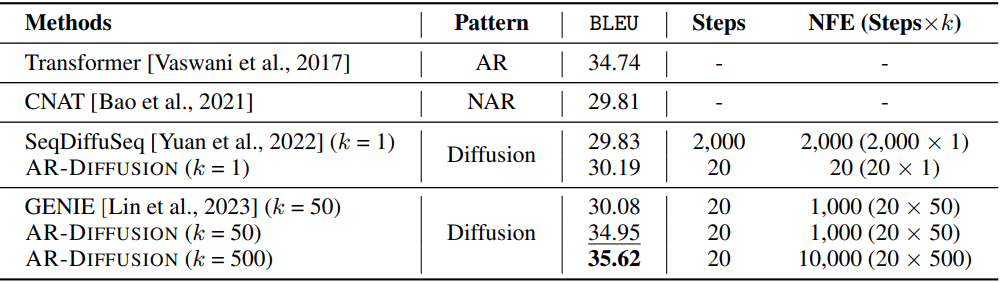
다음은 IWSLT14 test set에서의 SacreBLEU를 비교한 표이다.
Common Sense Generation
다음은 CommonGen dev set에서의 결과이다.
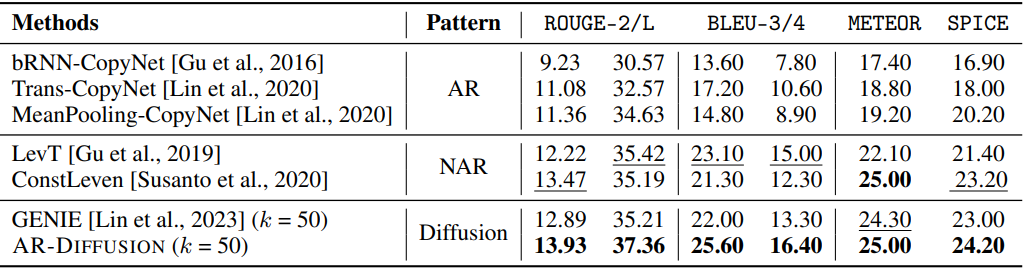
2. Inference Efficiency
다음은 XSUM test set에서 2 step이나 3 step으로 inference한 결과를 GENIE와 비교한 표이다.
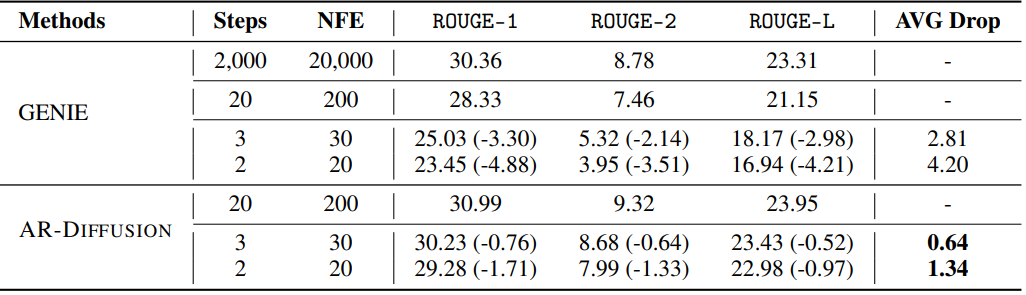
3. Analysis
Diversity of Samples
다음은 XSUM 테스트셋에서 생성된 10개 샘플의 다양성을 비교한 표이다.

Ablation Study
다음은 ablation study 결과이다.
Case Study
다음은 총 20 step으로 텍스트를 생성할 때 AR-Diffusion의 중간 상태이다. 색상의 밝기는 logit의 크기를 나타내며, 어두울수록 logit이 크다.

4. Impact of Minimum Bayes Risk and Anchor Point
Minimum Bayes Risk
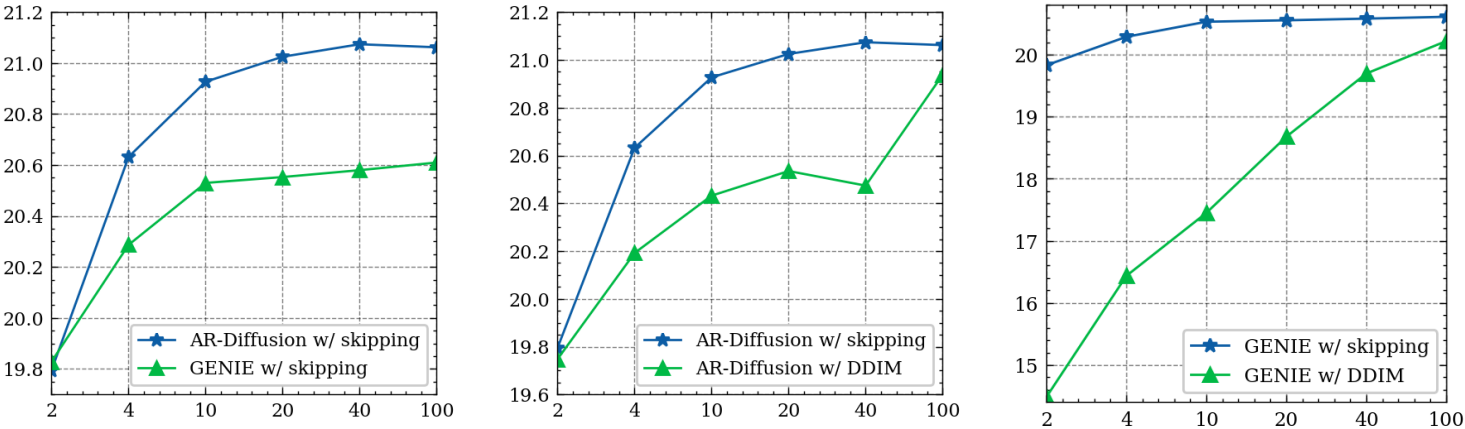
다음은 MBR 적용을 위한 후보 샘플 수와 SacreBLEU의 관계를 나타낸 그래프이다. (IWSLT14 DE $\rightarrow$ EN test set)

Anchor Point
다음은 다양한 위치에서 앵커 포인트의 효과를 나타낸 표이다. (IWSLT14 DE $\rightarrow$ EN test set)
