[논문리뷰] Analytic-Splatting: Anti-Aliased 3D Gaussian Splatting via Analytic Integration
ECCV 2024 (Oral). [Paper] [Page]
Zhihao Liang, Qi Zhang, Wenbo Hu, Ying Feng, Lei Zhu, Kui Jia
Beihang University | Chinese Academy of Sciences | Griffith University | RIKEN AIP | The University of Tokyo
17 Mar 2024
Introduction
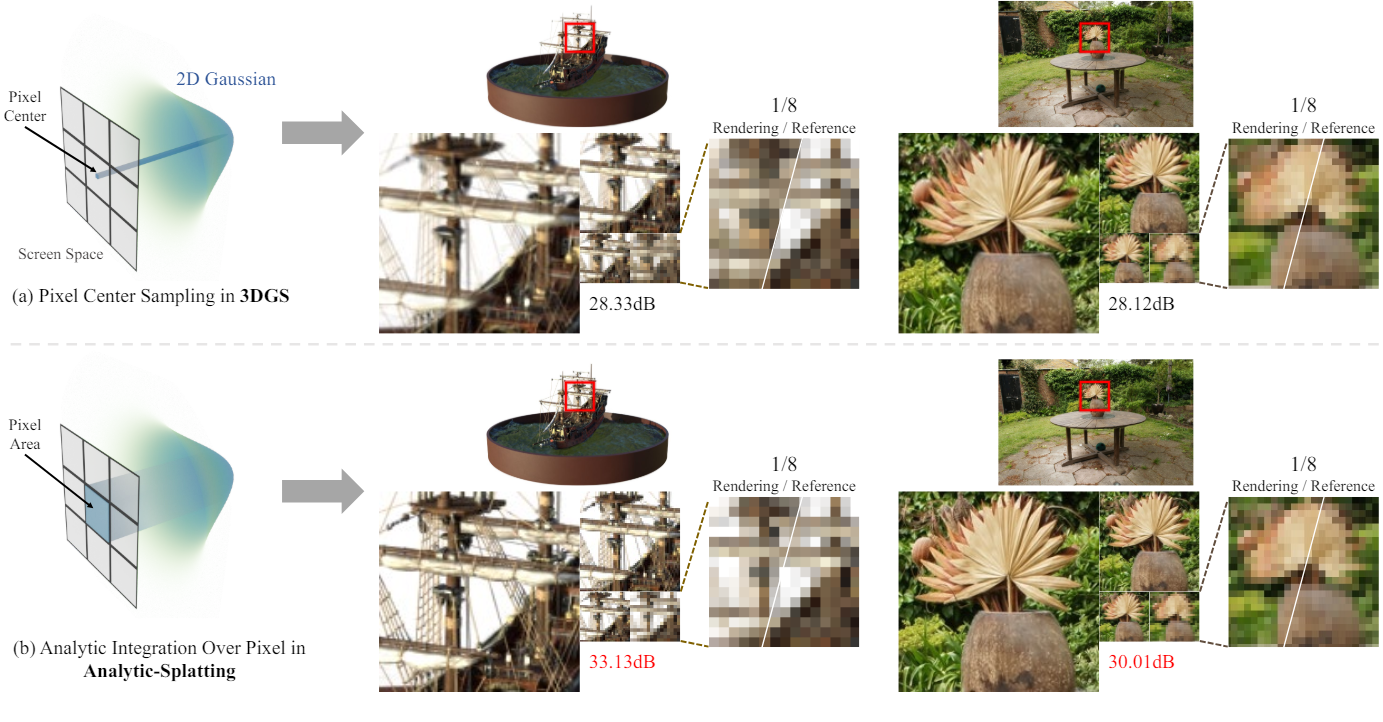
3D Gaussian Splatting는 일정한 해상도에서 장면 표현 학습 및 novel view synthesis에 사용된다. 그러나 멀티뷰 이미지들이 다양한 거리에서 캡처되거나 렌더링될 새로운 뷰가 캡처된 이미지의 해상도와 다른 경우 성능이 크게 저하된다. 주된 이유는 픽셀의 footprint가 서로 다른 해상도에서 변경되고 3DGS가 해당 Gaussian 값을 검색할 때 각 픽셀을 격리된 점, 즉 단순히 픽셀 중심으로 처리하기 때문에 이러한 변경에 둔감하다는 것이다. 결과적으로 3DGS는 특히 픽셀 공간이 급격하게 변경되는 경우(예: 확대 및 축소 효과를 사용하여 새로운 뷰 합성) 중요한 아티팩트(예: 흐릿하거나 톱니 모양)를 생성할 수 있다.
footprint: 화면 공간의 픽셀 window 영역과 world space의 해당 Gaussian 신호 영역 간의 비율로 정의
세부 사항을 살펴보면 3DGS는 이미지 공간에서 α 혼합 2D 가우시안 세트로 연속 신호를 나타내고 픽셀 셰이딩은 각 픽셀 영역 내에서 신호 응답을 통합하는 프로세스라는 것을 알 수 있다. 3DGS의 아티팩트는 잘못된 응답을 검색하는 Gaussian의 제한된 샘플링 대역폭으로 인해 발생하며, 특히 픽셀 공간이 크게 변경되는 경우 더욱 그렇다. 이 문제를 완화하기 위해 샘플링 대역폭을 늘리거나 (ex. 슈퍼 샘플링을 통해) 사전 필터링 기술을 사용할 수 있다. 예를 들어, Mip-Splatting은 사전 필터링 기술을 사용하고 2D 및 3D Gaussian의 고주파 성분을 정규화하여 안티앨리어싱을 달성하는 하이브리드 필터링 메커니즘을 제안하였다. Mip-Splatting은 3DGS에서 대부분의 앨리어싱을 극복하지만 디테일을 캡처하는 데 제한이 있고 지나치게 스무딩된 결과를 합성한다. 결과적으로 픽셀 window 영역 내에서 Gaussian 신호의 적분을 사용하는 것은 안티앨리어싱과 디테일 캡처 모두에 중요하다.
본 논문에서는 3DGS의 픽셀 셰이딩을 다시 살펴보고 안티앨리어싱을 위한 Gaussian 신호의 픽셀 window에서의 적분에 대한 해석적 근사치를 도입하였다. 3DGS의 discrete한 샘플링과 Mip-Splatting의 사전 필터링 대신 각 픽셀 영역 내의 적분을 해석적으로 근사한다. 본 논문의 방법을 Analytic-Splatting이라고 부른다. 픽셀 window를 2D Gaussian low-pass filter로 근사화하는 Mip-Splatting과 비교하여 제안한 방법은 Gaussian 신호의 고주파 성분을 억제하지 않으며 고품질 디테일을 더 잘 보존할 수 있다. Analytic-Splatting은 3DGS와 기타 방법에 존재하는 앨리어싱을 제거하는 동시에 더 나은 충실도로 더 많은 디테일을 합성하는 것으로 나타났다.
Preliminary
3DGS는 3D 장면을 점들의 집합 \(\{\textbf{p}_i\}_{i=1}^N\)로 명시적으로 나타낸다. 임의의 포인트 \(\textbf{p} \in \{\textbf{p}_i\}_{i=1}^N\)이 주어지면 3DGS는 이를 평균 벡터 $\boldsymbol{\mu}$와 공분산 행렬 $\boldsymbol{\Sigma}$를 사용하여 3D Gaussian 신호로 모델링한다.
\[\begin{equation} g^\textrm{3D} (\textbf{x} \vert \boldsymbol{\mu}, \boldsymbol{\Sigma}) = \exp \bigg( -\frac{1}{2} (\textbf{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\textbf{x} - \boldsymbol{\mu}) \bigg) \end{equation}\]여기서 $\mu \in \mathbb{R}^3$은 포인트 $\textbf{p}$의 위치이고, $\boldsymbol{\Sigma} \in \mathbb{R}^{3 \times 3}$은 공분산 행렬이며 $\boldsymbol{\Sigma} = \textbf{R} \textbf{S} \textbf{S}^\top \textbf{R}^\top$로 스케일링 행렬 $\textbf{S}$와 회전 행렬 $\textbf{R}$로 분해된다. $\textbf{S}$는 $3 \times 3$ 대각 행렬을 나타내고 $\textbf{R}$은 단위 quaternion $\textbf{q}$로 구성된 $3 \times 3$ 행렬이다.
Extrinsic matrix $\textbf{T}$와 projection matrix $\textbf{K}$를 사용한 viewing transformation이 주어지면 2D 화면 공간에서 투영된 위치 $\hat{\boldsymbol{\mu}}$ 및 공분산 행렬 $\hat{\boldsymbol{\Sigma}}$를 다음과 같이 얻는다.
\[\begin{equation} \hat{\boldsymbol{\mu}} = \textbf{K} \textbf{T} [\boldsymbol{\mu}, 1]^\top \quad \hat{\Sigma} = \textbf{J} \textbf{T} \boldsymbol{\Sigma} \textbf{T}^\top \textbf{J}^\top \end{equation}\]여기서 $\textbf{J}$는 perspective projection의 affine approximation의 Jacobian matrix이다. 3DGS는 $\hat{\boldsymbol{\mu}}$와 $\hat{\boldsymbol{\Sigma}}$의 second-order 값만 각각 $\hat{\boldsymbol{\mu}} \in \mathbb{R}^2$와 $\hat{\boldsymbol{\Sigma}} \in \mathbb{R}^{2 \times 2}$로 유지한다. 픽셀 $\textbf{u}$에 대해 투영된 2D Gaussian은 다음과 같다.
\[\begin{equation} g^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}, \hat{\boldsymbol{\Sigma}}) = \exp \bigg( -\frac{1}{2} (\textbf{u} - \hat{\boldsymbol{\mu}})^\top \hat{\boldsymbol{\Sigma}}^{-1} (\textbf{u} - \hat{\boldsymbol{\mu}}) \bigg) \end{equation}\]투영된 2D Gaussian 신호를 사용하여 3DGS는 투과율을 도출하고 다음 식을 통해 픽셀 $\textbf{u}$의 색상을 계산한다.
\[\begin{equation} \textbf{C}(\textbf{u}) = \sum_{i \in N} T_i g_i^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}_i, \hat{\boldsymbol{\Sigma}}_i) \alpha_i c_i, \\ T_i = \prod_{j=1}^{i-1} (1 - g_j^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}_j, \hat{\boldsymbol{\Sigma}}_j) \alpha_j) \end{equation}\]여기서 첨자 $i$가 있는 기호는 점 \(\textbf{p}_i\)와 관련된 속성을 나타낸다.
$\hat{\boldsymbol{\Sigma}}$가 real-symmetric $2 \times 2$ 행렬이라는 점을 고려하면 $\hat{\boldsymbol{\Sigma}}$와 $\hat{\boldsymbol{\Sigma}}^{-1}$을 수치적으로 표현하면 다음과 같다.
\[\begin{equation} \hat{\boldsymbol{\Sigma}} = \begin{bmatrix} \hat{\Sigma}_{11} & \hat{\Sigma}_{12} \\ \hat{\Sigma}_{12} & \hat{\Sigma}_{22} \end{bmatrix}, \quad \hat{\boldsymbol{\Sigma}}^{-1} = \frac{1}{\vert \hat{\boldsymbol{\Sigma}} \vert} \begin{bmatrix} \hat{\Sigma}_{22} & -\hat{\Sigma}_{12} \\ -\hat{\Sigma}_{12} & \hat{\Sigma}_{11} \end{bmatrix} = \begin{bmatrix} a & b \\ b & c \end{bmatrix} \\ a = \frac{\hat{\Sigma}_{22}}{\vert \hat{\boldsymbol{\Sigma}} \vert}, \quad b = -\frac{\hat{\Sigma}_{12}}{\vert \hat{\boldsymbol{\Sigma}} \vert}, \quad c = \frac{\hat{\Sigma}_{11}}{\vert \hat{\boldsymbol{\Sigma}} \vert} \end{equation}\]2D 화면 공간에서 픽셀 $\textbf{u} = [u_x, u_y]^\top$이고 투영된 위치 \(\hat{\boldsymbol{\mu}} = [\hat{\mu}_x, \hat{\mu}_y]^\top\)라고 가정하면 $g^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}, \hat{\boldsymbol{\Sigma}})$은 다음과 같이 다시 쓸 수 있다.
\[\begin{equation} g^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}, \hat{\boldsymbol{\Sigma}}) = \exp \bigg( -\frac{a}{2} \hat{u}_x^2 - \frac{c}{2} \hat{u}_y^2 - b \hat{u}_x \hat{u}_y \bigg), \\ \hat{u}_x = u_x - \hat{\mu}_x, \quad \hat{u}_y = u_y - \hat{\mu}_y \end{equation}\]위 식에 표시된 것처럼 3DGS가 해당 Gaussian 값을 계산할 때 각 픽셀을 격리된 하나의 점으로 처리한다는 점은 주목할 가치가 있다. 이 근사 방식은 상대적으로 일관된 거리에서 장면 콘텐츠를 캡처하기 위해 이미지를 학습하고 테스트할 때 효과적으로 작동한다. 그러나 초점 거리 또는 카메라 거리 조정으로 인해 픽셀 공간이 변경되면 3DGS 렌더링은 확대 중에 관찰되는 얇은 Gaussian과 같은 상당한 아티팩트를 나타낸다. 결과적으로 픽셀을 window 영역으로 정의하고 해당 영역을 계산하는 것이 중요하다. 이 영역 내에서 Gaussian 신호를 통합하여 계산해야 한다. 직관적이지만 시간이 많이 걸리는 슈퍼 샘플링을 사용하는 것보다 Gaussian 신호가 연속 함수라는 점을 고려하면 문제를 보다 해석적으로 해결하는 것이 좋다.
Methods
앞서 3DGS가 각 픽셀의 window 영역을 무시하고 픽셀 중심에 해당하는 Gaussian 값만 간주한다는 것을 관찰했다. 이 접근 방식은 서로 다른 해상도에서 픽셀 공간의 변동으로 인해 필연적으로 아티팩트를 생성한다. 본 논문은 픽셀의 신호를 정확하게 설명하여 이 문제를 해결하기 위해 픽셀 window 영역 내에서 2D Gaussian 신호의 해석적 근사치를 도출하였다. 이후에 유도된 적분을 적용하여 3DGS 프레임워크에서 $g^\textrm{2D}$를 대체하였다.
1. Revisit One-dimensional Gaussian Signal Response
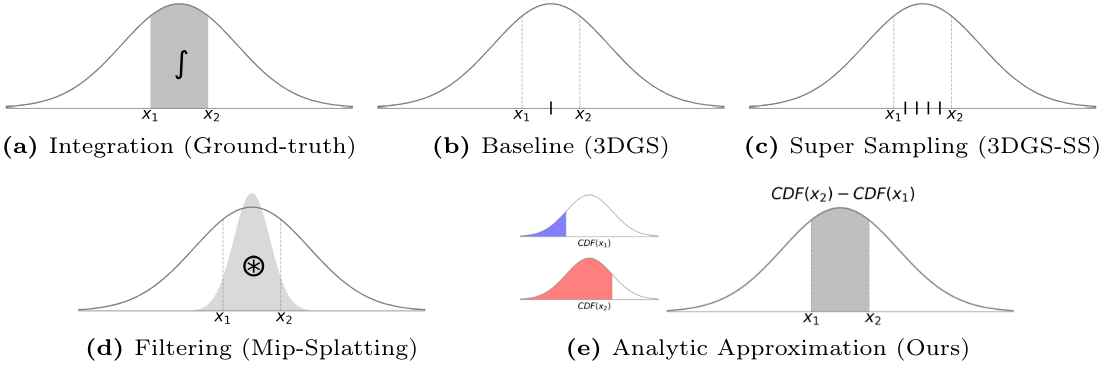
먼저 이해를 돕기 위해 window 영역 내 1D Gaussian 신호의 통합 응답 예제를 다시 살펴보자. 신호 $g(x)$와 window 영역이 주어지면 위의 (a)에 표시된 대로 이 도메인 내에서 신호 \(\mathcal{I}_g = \int_{x_1}^{x_2} g(x)dx\)를 통합하여 응답을 얻는 것을 목표로 한다. 알 수 없는 신호의 경우, (b)와 (c)에서 설명된대로 window 영역 내의 몬테카를로 샘플링은 적분을 근사화하는 실행 가능한 접근 방식이며, 근사 결과는 샘플 수 $N$이 증가할수록 더 정확해진다. 그럼에도 불구하고 샘플 수를 늘리면 (즉, 슈퍼 샘플링) 계산 부담이 크게 늘어난다.
다행스럽게도 3DGS 프레임워크의 목표는 window 영역 내에서 Gaussian 신호의 응답을 얻는 것이다. Gaussian 신호가 연속적인 실수 값 함수라는 점을 고려하면 (b)나 (c)같은 수치적 적분(numerical integration)에 비해 더 정확한 Gaussianu 정적분에 대한 해석적 근사치를 도출하는 것이 당연하다. 예를 들어, Mip-Splatting에서는 window 영역을 Gaussian kernel $g_w$로 처리하고, (d)와 같이 Gaussian kernel로 Gaussian 신호를 convolution한 후 샘플링 결과로 적분을 근사화한다. 이 사전 필터링은 Gaussian 신호의 convolution 특성을 사용하지만, 이 근사는 Gaussian 신호 $g$가 주로 고주파 성분으로 구성되는 경우, 즉 표준편차 $\sigma$가 작은 경우에 큰 차이를 생긴다.
이러한 단점을 극복하기 위해 window 영역 내 적분을 해석적으로 계산해야 한다. 특히, $[x_1, x_2]$ 내의 정적분을 계산하는 문제는 미적분의 기본 정리 1을 적용하여 두 개의 이상 적분을 빼는 것으로 단순화될 수 있다. $G(x)$를 다음과 같이 정의된 표준 Gaussian 분포 $g(x)$의 누적 분포 함수(CDF)로 설정한다.
\[\begin{equation} G(x) = \int_{-\infty}^x g(x) dx, \quad g(x) = \frac{1}{\sqrt{2 \pi}} \exp \bigg( - \frac{x^2}{2} \bigg) \end{equation}\]$[x_1, x_2]$ 내에서 $g(x)$의 정적분은 다음과 같이 표현될 수 있다.
\[\begin{equation} \mathcal{I}_g = G(x_2) - G(x_1) \end{equation}\]그러나 Gaussian function의 CDF는 closed-form이 아니다. 그렇기 때문에 표준편차가 $\sigma = 1$일때 CDF $G(x)$를 다음과 같은 logistic function $S(x)$로 근사화한다.
\[\begin{equation} S(x) = \frac{1}{1 + \exp (-1.6x - 0.07 x^3)} \end{equation}\]이 근사에는 CDF $G(x)$의 유사한 속성도 포함되어 있다.
- $S(x)$는 감소하지 않으며 우연속(right-continuous)이며, $-\infty$로 갈 때 0으로 수렴하고 $+\infty$로 갈 때 1로 수렴한다.
- $S(x)$의 곡선은 점 $(0, 1/2)$을 중심으로 2-fold 회전 대칭이다.
표준편차가 다른 Gaussian 신호의 경우 표준편차의 역수 $1 / \sigma$로 $S(x)$의 $x$를 스케일링하여 CDF를 근사화할 수 있다. $S(x)$의 $x$가 $1 / \sigma$만큼 스케일링되면 이를 $S_\sigma (x)$로 표현한다.
\[\begin{aligned} G_\sigma (x) &= \int_{-\infty}^x \frac{1}{\sigma \sqrt{2 \pi}} \exp \bigg( - \frac{u^2}{2 \sigma^2} \bigg) du \\ &\approx S_\sigma (x) = S \bigg( \frac{x}{\sigma} \bigg) = \frac{1}{1 + \exp (-1.6 (x / \sigma) - 0.07 (x / \sigma)^3)} \end{aligned}\]샘플 $u$가 주어지면 $[u - \frac{1}{2}, u + \frac{1}{2}]$ 영역 내의 Gaussian 신호 $g(x)$의 적분 \(\mathcal{I}_g (u)\)는 다음과 같이 정의된다.
\[\begin{equation} \mathcal{I}_g (u) = \int_{u - \frac{1}{2}}^{u + \frac{1}{2}} g(x) dx = G(u + \frac{1}{2}) - G(u - \frac{1}{2}) \end{equation}\]이를 $S(x)$로 근사하면 다음과 같다.
\[\begin{equation} \mathcal{I}_g (u) \approx S(u + \frac{1}{2}) - S(u - \frac{1}{2}) \end{equation}\]2. Analytic-Splatting
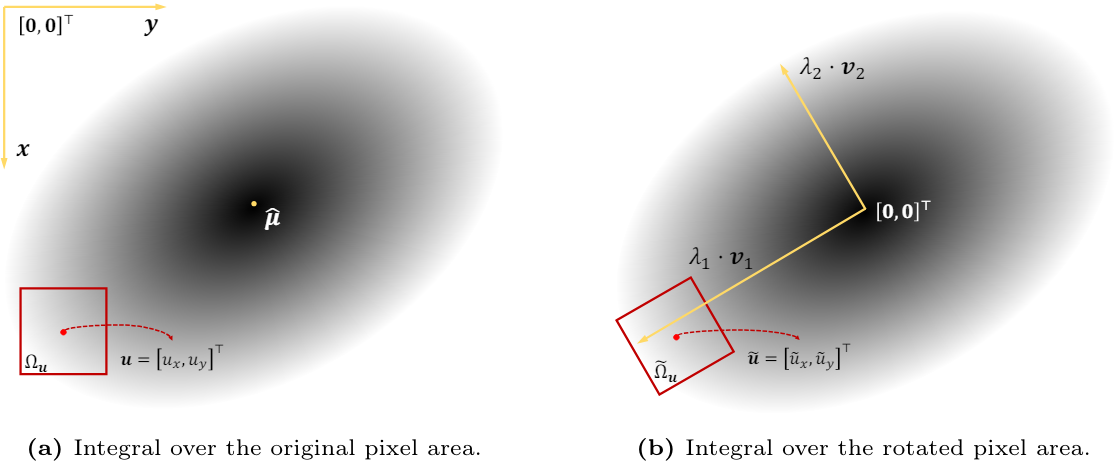
수학적으로 $g^\textrm{2D} (\textbf{u})$를 근사 적분 \(\mathcal{I}_g^\textrm{2D} (\textbf{u})\)로 대체한다. 위 그림의 (a)와 같이 window 영역 \(\Omega_\textbf{u}\)에 해당하는 2D 화면 공간의 픽셀 $\textbf{u} = [u_x, u_y]^\top$에 대해 Gaussian 신호 적분은 다음과 같이 표현된다.
이 적분에서 correction term을 처리하는 것은 다루기 어렵다. Correction term을 풀고 적분을 풀기 위해 2D Gaussian $g^\textrm{2D}$의 공분산 행렬 $\hat{\boldsymbol{\Sigma}}$를 대각화하고 위 그림의 (b)와 같이 적분 영역을 약간 회전시켜 두 개의 독립적인 1D Gaussian 적분을 곱하여 적분을 근사화한다.
구체적으로, 먼저 공분산 행렬 $\hat{\boldsymbol{\Sigma}}$에 대해 eigenvalue decomposition을 수행하여 eigenvalue \(\{\lambda_1, \lambda_2\}\)와 eigenvector \(\{\textbf{v}_1, \textbf{v}_2\}\)를 얻는다. 대각화 후에는 더 나은 설명을 위해 $\hat{\boldsymbol{\mu}} = [\hat{\mu}_x, \hat{\mu}_y]^\top$를 원점으로 하고 \(\{\textbf{v}_1, \textbf{v}_2\}\)를 축으로 사용하여 새로운 좌표계를 구성한다.
이 좌표계에서 픽셀 $\textbf{u} = [u_x, u_y]^\top$가 주어지면 $g^\textrm{2D}$를 두 개의 독립적인 1D Gaussian의 곱으로 다시 쓴다.
\[\begin{aligned} g^\textrm{2D} (\textbf{u}) &= \exp \bigg( - \frac{1}{2 \lambda_1} \tilde{u}_x^2 - \frac{1}{2 \lambda_2} \tilde{u}_y^2 \bigg) = \exp \bigg( - \frac{1}{2 \lambda_1} \tilde{u}_x^2 \bigg) \exp \bigg( - \frac{1}{2 \lambda_2} \tilde{u}_y^2 \bigg) \\ \tilde{\textbf{u}} &= \begin{bmatrix} \tilde{u}_x \\ \tilde{u}_y \end{bmatrix} = \begin{bmatrix} - \textbf{v}_1 - \\ - \textbf{v}_2 - \end{bmatrix} (\textbf{u} - \hat{\boldsymbol{\mu}}) = \begin{bmatrix} - \textbf{v}_1 - \\ - \textbf{v}_2 - \end{bmatrix} \begin{bmatrix} u_x - \hat{\mu}_x \\ u_y - \hat{\mu}_y \end{bmatrix} \end{aligned}\]여기서 $\tilde{\textbf{u}} = [\tilde{u}_x, \tilde{u}_y]^\top$는 픽셀 중심의 대각화된 좌표이다. 대각화 후에는 픽셀 중심을 따라 적분 영역 \(\Omega_\textbf{u}\)를 추가로 회전하여 eigenvector와 정렬하고 적분을 근사화하기 위한 \(\tilde{\Omega}_\textbf{u}\)를 얻는다. 따라서 적분은 다음과 같이 근사화될 수 있다.
\[\begin{aligned} \mathcal{I}_g^\textrm{2D} (\textbf{u}) &\approx \int_{\tilde{\Omega}_\textbf{u}} g^\textrm{2D} (\textbf{u}) d \textbf{u} \\ &= \int_{\tilde{u}_x - \frac{1}{2}}^{\tilde{u}_x + \frac{1}{2}} \exp \bigg(- \frac{1}{2 \lambda_1} x^2 \bigg) dx \int_{\tilde{u}_y - \frac{1}{2}}^{\tilde{u}_y + \frac{1}{2}} \exp \bigg(- \frac{1}{2 \lambda_2} y^2 \bigg) dy \\ &= 2 \pi \sqrt{\lambda_1 \lambda_2} \int_{\tilde{u}_x - \frac{1}{2}}^{\tilde{u}_x + \frac{1}{2}} \frac{1}{\sqrt{2\pi \lambda_1}} \exp \bigg(- \frac{1}{2 \lambda_1} x^2 \bigg) dx \int_{\tilde{u}_y - \frac{1}{2}}^{\tilde{u}_y + \frac{1}{2}} \frac{1}{\sqrt{2\pi \lambda_2}} \exp \bigg(- \frac{1}{2 \lambda_2} y^2 \bigg) dy \\ &\approx 2 \pi \sigma_1 \sigma_2 \bigg[ S_{\sigma_1} (\tilde{u}_x + \frac{1}{2}) - S_{\sigma_1} (\tilde{u}_x - \frac{1}{2}) \bigg] \bigg[ S_{\sigma_2} (\tilde{u}_y + \frac{1}{2}) - S_{\sigma_2} (\tilde{u}_y - \frac{1}{2}) \bigg] \end{aligned}\]여기서 $\sigma_1 = \sqrt{\lambda_1}$이고 $\sigma_2 = \sqrt{\lambda_2}$이다.
요약하면 Analytic-Splatting의 volume shading은 다음과 같다.
\[\begin{aligned} \textbf{C} (\textbf{u}) &= \sum_{i \in N} T_i \mathcal{I}_{g-i}^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}_i, \hat{\boldsymbol{\Sigma}}_i) \alpha_i c_i, \quad T_i = \prod_{j=1}^{i-1} (1 - \mathcal{I}_{g-j}^\textrm{2D} (\textbf{u} \vert \hat{\boldsymbol{\mu}}_j, \hat{\boldsymbol{\Sigma}}_j) \alpha_j) \\ \mathcal{I}_g^\textrm{2D} (\textbf{u}) &= 2 \pi \sigma_1 \sigma_2 \bigg[ S_{\sigma_1} (\tilde{u}_x + \frac{1}{2}) - S_{\sigma_1} (\tilde{u}_x - \frac{1}{2}) \bigg] \bigg[ S_{\sigma_2} (\tilde{u}_y + \frac{1}{2}) - S_{\sigma_2} (\tilde{u}_y - \frac{1}{2}) \bigg] \end{aligned}\]Experiments
1. Approximation Error Analysis
다음은 logistic function $S(x)$와 CDF $G(x)$의 차이를 표준편차 $\sigma$에 따라 비교한 그래프이다.
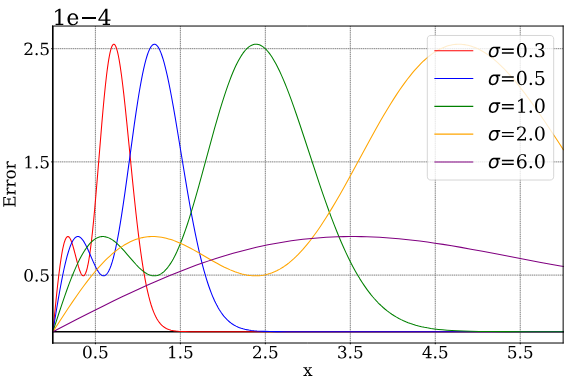
다음은 근사 적분값 $S(x + \frac{1}{2}) - S(x - \frac{1}{2})$와 실제 적분값 $G(x + \frac{1}{2}) - G(x - \frac{1}{2})$의 차이를 $\sigma$에 따라 비교한 그래프이다.
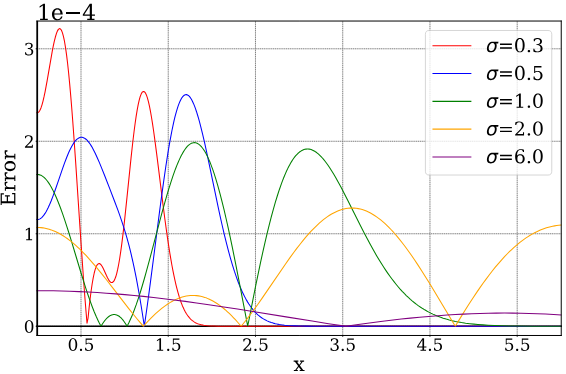
다음은 표준편차 $\sigma$에 따른 근사 오차를 다른 방법들과 비교한 그래프이다.
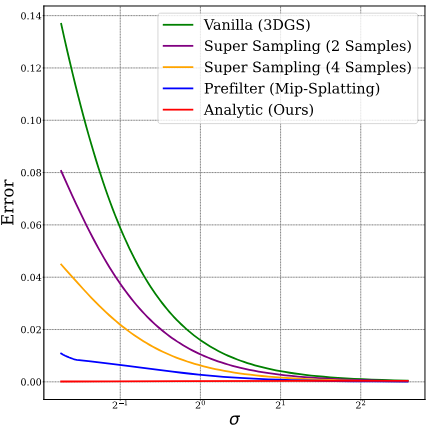
다음은 변수 분포에 따른 근사 오차를 다른 방법들과 비교한 그래프이다.
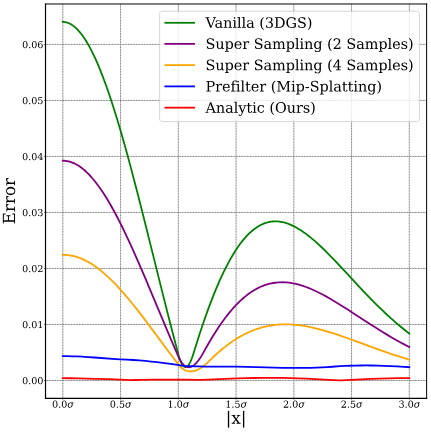
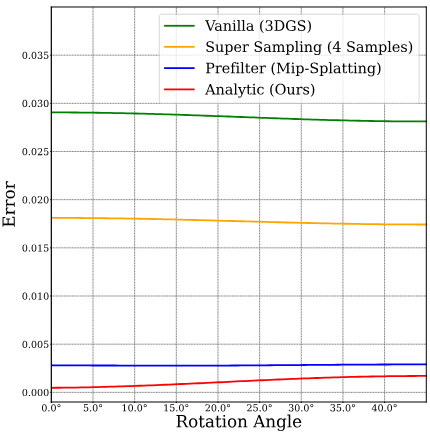
다음은 적분 영역을 회전시킨 각도에 따른 근사 오차를 다른 방법들과 비교한 그래프이다.
2. Comparison
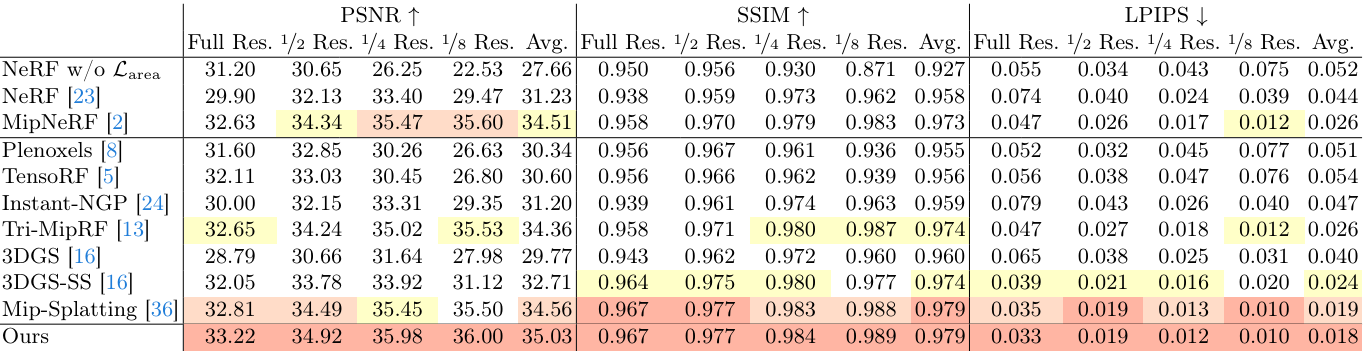
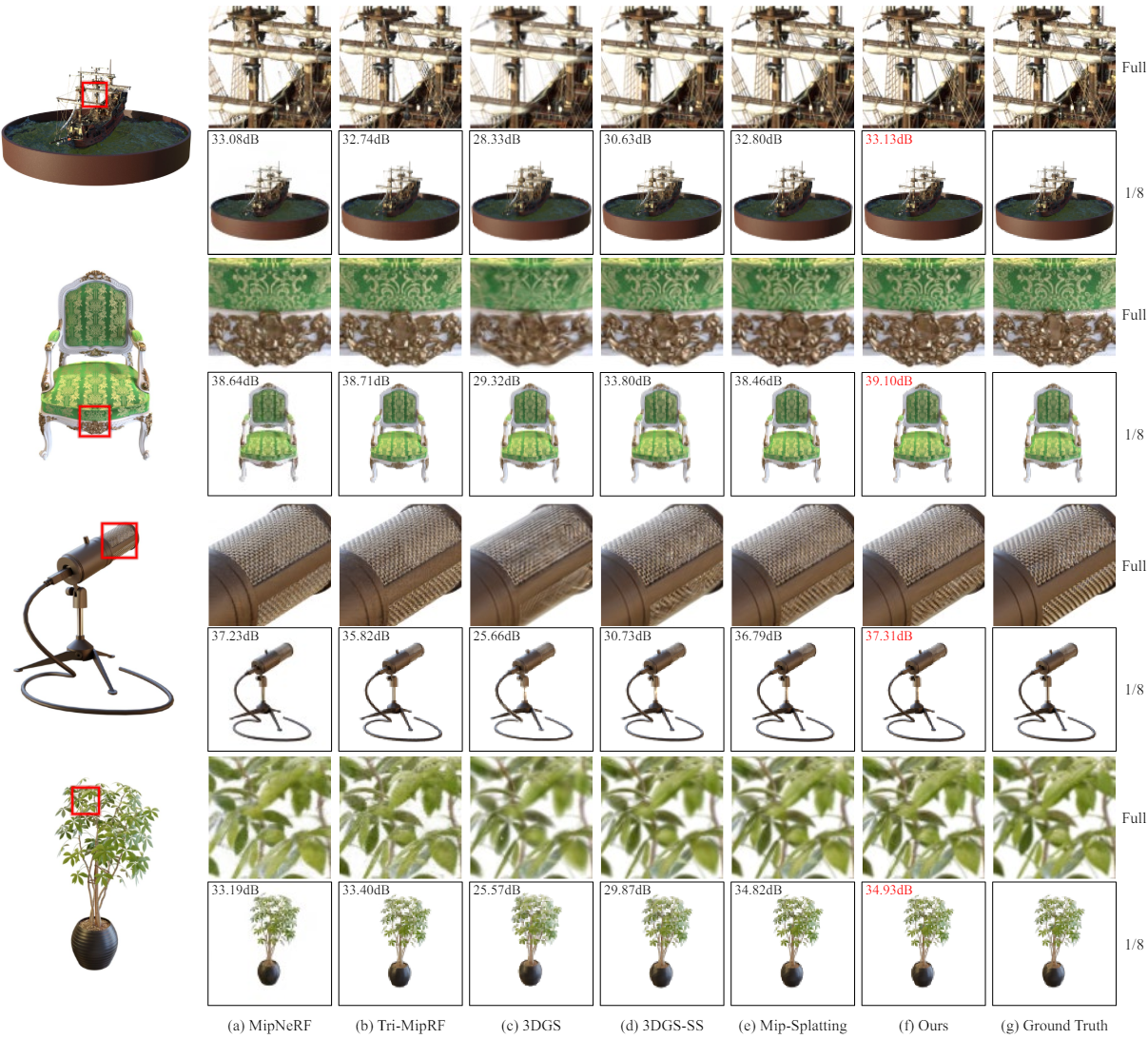
다음은 Blender 합성 데이터셋에서의 성능을 다른 방법들과 비교한 결과이다.
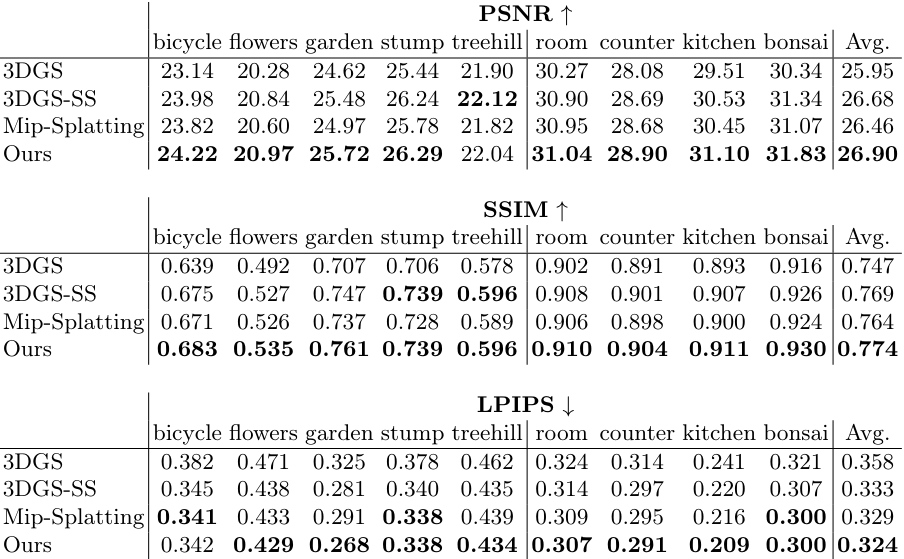
다음은 Mip-NeRF 360 데이터셋에서의 성능을 다른 방법들과 비교한 결과이다.


다음은 Mip-NeRF 360 데이터셋에서의 super-resolution을 다른 방법들과 비교한 결과이다.