[BLOG 리뷰] AI achieves silver-medal standard solving International Mathematical Olympiad problems
[Blog]
Google DeepMind
25 Jul 2024

Introduction
고급 수학적 추론을 갖춘 인공 일반 지능(AGI)은 과학과 기술의 새로운 지평을 열 잠재력이 있다. 현재의 AI 시스템은 추론 기술과 학습 데이터의 한계로 인해 여전히 일반적인 수학 문제를 해결하는 데 어려움을 겪고 있다. Google DeepMind는 형식적 수학 추론을 위한 새로운 강화 학습 기반 시스템인 AlphaProof와 기하 풀이 시스템의 개선된 버전인 AlphaGeometry 2를 공개하였다. 이 시스템들은 올해의 국제 수학 올림피아드(IMO)에서 6개 문제 중 4개를 해결하여 처음으로 IMO에서 은메달리스트와 동일한 수준을 달성했다.
먼저, 주어진 문제들은 시스템이 이해할 수 있도록 수동으로 형식적 수학 언어로 번역되었다. DeepMind의 시스템은 한 문제를 몇 분 안에 풀었고 다른 문제를 푸는 데 최대 3일이 걸렸다. AlphaProof는 답을 결정하고 그것이 옳다는 것을 증명함으로써 두 개의 대수 문제와 한 개의 정수론 문제를 풀었다. 여기에는 올해 IMO에서 단 5명의 참가자만이 푼 대회에서 가장 어려운 문제가 포함되어 있다. AlphaGeometry 2는 기하학 문제를 증명했다. 두 개의 조합 문제는 풀지 못했다.
문제는 총 6개이고 각각 최대 7점을 얻을 수 있으며, 총점은 42점이다. DeepMind의 시스템은 최종 점수 28점을 달성하였으며, 해결한 각 문제에서 완벽한 점수를 받았다. 이는 은메달 부문의 최고 점수와 같다. 올해 금메달 기준은 29점에서 시작하며, 609명의 참가자 중 58명이 달성했다.
AlphaProof
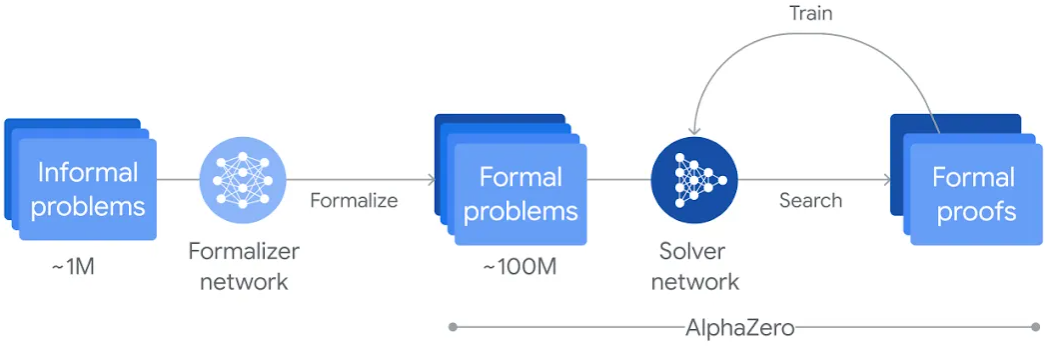
AlphaProof는 형식적 언어인 Lean에서 수학적 명제를 증명하도록 스스로를 학습시키는 시스템이다. 사전 학습된 언어 모델을 AlphaZero 강화 학습 알고리즘과 결합한다. AlphaZero는 이전에 체스, 쇼기, 바둑 게임을 마스터하는 방법을 스스로 학습했다.
형식적 언어는 수학적 추론을 포함하는 증명이 정확성을 위해 형식적으로 검증될 수 있다는 중요한 이점을 제공한다. 그러나 이전에는 인간이 작성한 데이터의 양이 매우 제한적이어서 머신러닝에서 사용하는 데 제약을 받았다. 반면, 자연어 기반 접근법은 수십 배 더 많은 데이터에 액세스할 수 있음에도 불구하고 그럴듯하지만 잘못된 중간 추론 단계와 답을 생성할 수 있다. 저자들은 Gemini 모델을 fine-tuning하여 자연어 명제를 자동으로 형식적 명제로 변환하고 다양한 난이도의 형식적 문제 라이브러리를 생성하여 이 두 보완적인 영역 사이에 다리를 놓았다.
문제가 제시되면 AlphaProof는 정답 후보를 생성한 다음 Lean에서 가능한 증명 단계를 검색하여 이를 증명하거나 반증한다. 발견되고 검증된 각 증명은 AlphaProof의 언어 모델을 강화하는 데 사용되어 이후의 더 어려운 문제를 해결하는 능력을 향상시킨다.
저자들은 IMO에 앞서 몇 주 동안 광범위한 난이도와 수학적 주제를 포괄하는 수백만 개의 문제를 증명하거나 반증하여 AlphaProof를 학습시켰다. 학습 루프는 대회 중에도 적용되어 전체 정답을 찾을 때까지 대회 문제의 자체 생성된 변형에 대한 증명을 강화했다.
AlphaGeometry 2
AlphaGeometry 2는 AlphaGeometry를 상당히 개선한 버전이다. 언어 모델은 Gemini를 기반으로 하고 AlphaGeometry보다 훨씬 더 많은 합성 데이터로 처음부터 학습하였다. 이를 통해 모델은 훨씬 더 어려운 기하학 문제를 해결하는 데 도움이 되었다.
AlphaGeometry 2는 이전 버전보다 두 자릿수 더 빠른 심볼릭 엔진을 사용한다. 새로운 문제가 제시되면 새로운 knowledge-sharing 메커니즘을 사용하여 다양한 search tree의 고급 조합을 통해 더 복잡한 문제를 해결할 수 있다.
올해 IMO 이전에 AlphaGeometry 2는 지난 25년 동안의 모든 IMO 기하학 문제의 83%를 풀었는데, 이는 AlphaGeometry가 달성한 53%의 비율과 비교된다. IMO 2024의 경우 AlphaGeometry 2는 형식화된 후 19초 이내에 문제 4를 풀었다.
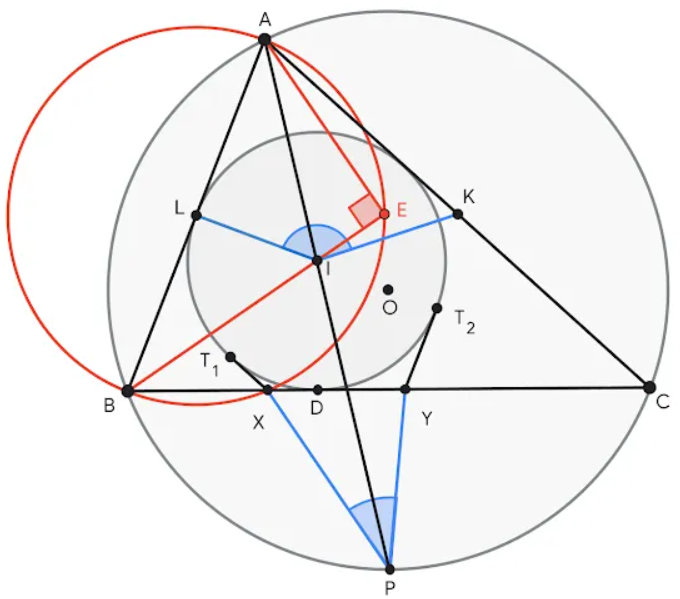
위 그림은 ∠KIL과 ∠XPY의 합이 180°임을 증명하는 문제 4이다. AlphaGeometry 2는 ∠AEB = 90°가 되도록 선 BI에 있는 점 E를 구성하는 것을 제안했다. 점 E는 결론을 증명하는 데 필요한 ABE ~ YBI, ALE ~ IPC와 같은 여러 닮은 삼각형 쌍들을 생성한다.