[논문리뷰] Improving Diffusion-based Image Translation using Asymmetric Gradient Guidance (AGG)
arXiv 2023. [Paper]
Gihyun Kwon, Jong Chul Ye
KAIST
7 Jun 2023

Introduction
Image translation은 원본 이미지의 구조적 속성을 유지하면서 이미지를 원본 도메인에서 타겟 도메인으로 변환하는 것을 목표로 하는 task이다. 과거에는 GAN 기반의 image translation 방법이 주로 사용되었으며, 단일 모드 image-to-image translation (I2I) 모델부터 다중 모드 I2I 모델까지 다양했다. 이러한 방법들은 좋은 성능을 보였지만 임의의 도메인과 조건에 대해 I2I를 수행할 수 없다는 단점이 있었다.
최근에는 이러한 문제를 해결하기 위한 다양한 방법이 제안되고 있다. 특히 주목할만한 것은 원하는 조건으로 이미지를 생성하기 위해 수정을 적용하여 사전 학습된 생성 모델의 생성 프로세스를 조작하는 방법이다. 이 접근 방식은 원하는 이미지를 생성할 수 있으면서도 사전 학습된 모델의 우수한 생성 성능을 사용할 수 있다는 장점이 있다. 특히, 이전 방법들은 이미지 조작을 가능하게 하기 위해 사전 학습된 GAN 모델을 주로 사용했다. 최근에는 텍스트 조건에 기반한 이미지 편집을 위해 대규모 기반 모델, 특히 CLIP과 같은 text-to-image 임베딩 모델의 사용이 도입되었다. 그러나 이러한 방법들은 제한된 도메인과 실제 이미지를 latent space에 삽입하는 번거로운 과정과 같은 GAN 모델의 한계로 인해 제한된 성능을 보인다.
Diffusion model의 발전과 텍스트 인코더 모델의 결합으로 text-to-image diffusion model이 개발되었고, diffusion model을 이용한 image translation과 이미지 편집에 대한 연구가 활발해졌다. 특히 텍스트 조건과의 교차주의를 기반으로 다양한 방법이 제안되어 이미지 대 이미지 번역이 가능하다. 그러나 text-to-image 모델은 원본 이미지를 latent space에 정확하게 삽입하는 inversion process가 필요하므로 최적화를 위해 추가 시간이 필요하다. 또한 원본 이미지를 조건으로 제공하는 image translation 케이스에 적용하기 어렵다.
이를 해결하기 위해 DiffuseIT은 타겟 스타일을 풀고 변경하는 동안 소스 이미지의 구조적 속성을 보존하기 위해 생성 프로세스 중에 gradient guidance를 사용한다. 이러한 모델은 우수한 성능을 보여주었지만 여전히 ViT 네트워크 슬라이싱과 계산 비용이 많이 드는 기울기 계산을 광범위하게 사용해야 한다.
본 논문은 기존 방법의 한계를 해결하기 위해 여기서는 다양한 모델의 강점을 융합하는 Asymmetric Gradient Guidance (AGG)를 사용하는 새로운 샘플링 접근 방식을 제시하였다. 특히, AGG에 의한 기울기 업데이트는 두 단계로 구성된다.
- 초기 업데이트를 계산하기 위한 단일 MCG 프레임워크
- Tweedie 공식에 의해 denoise된 신호에서 계산적으로 효율적인 Decomposed Diffusion Sampling (DDS) 업데이트
또한, ViT 기반 구조 보존 loss를 슬라이싱하는 DiffuseIT와 달리 forward DDIM step에서 저장된 중간 샘플을 사용하여 훨씬 간단한 구조 정규화 항을 사용한다. 간단한 정규화 loss와 효율적인 기울기 업데이트와 결합하여 텍스트 조건과 one-shot 이미지 조건에서 훨씬 빠르고 효과적인 image translation이 가능하다. 또한, 이 통합은 기존 이미지 diffusion model과 latent diffusion model 모두에서 작동하는 샘플링 방식을 가능하게 하므로 상당한 이점을 제공한다.
Background
1. Denoising Diffusion Probabilistic Models (DDPM)
DDPM은 Markovian forward process에 의해 생성된 noisy한 이미지 $x_t$에서 추가된 noise를 추정하도록 학습된다.
\[\begin{equation} q(x_T \vert x_0) := \prod_{t=1}^T q(x_t \vert x_{t-1}) \\ \textrm{where} \quad q(x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \end{equation}\]Reverse process의 경우, 학습된 noise 예측 네트워크 $\epsilon_\theta$를 사용하여 이전 timestep $x_{t−1}$의 noisy한 샘플을 예측할 수 있다.
\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t) \bigg) + \sigma_t z \\ \bar{\alpha}_t := \prod_{i=1}^t \alpha_t, \quad \alpha_t := 1 - \beta_t, \quad z \sim \mathcal{N}(0, I) \end{equation}\]반복 프로세스를 통해 초기 샘플 $x_T \sim \mathcal{N}(0, I)$에서 이미지 $x_0$을 샘플링할 수 있다.
2. Denoising Diffusion Implicit Models (DDIM)
Diffusion model에는 많은 step이 필요하기 때문에 전체 샘플링 프로세스가 느리다. 이 문제를 해결하기 위해 DDIM은 DDPM 공식을 non-Markovian process로 재정의하여 다른 방법을 제안한다. 구체적으로 reverse process는 다음과 같다.
\[\begin{equation} x_{t-1} = \underbrace{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \hat{x}_{0, t} (\epsilon_\theta (x_t, t))}_{\textrm{Denoise}} + \underbrace{D_t (\epsilon_\theta (x_t, t))}_{\textrm{Noise}} + \sigma_t z_t \\ \hat{x}_{0, t} (\epsilon_\theta (x_t, t)) := \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_\theta (x_t, t)}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \\ D_t (\epsilon_\theta (x_t, t)) := \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \epsilon_\theta (x_t, t) \end{equation}\]$\sigma_t = 0$이면 reverse process가 완전히 deterministic해지며, 빠른 샘플링이 가능해진다.
Main Contribution
조건부 diffusion 연구의 최근 초점은 reverse sampling 동안 컨디셔닝 기울기를 통합하는 방법이다. 이는 주어진 loss function $\ell (x)$에 대해 xt에서 계산된 loss의 기울기를 직접 주입하면 부정확한 gradient guidance가 생성되기 때문이다. 이를 해결하기 위해 다양한 방법이 개발되었다. 본 논문은 먼저 간략한 리뷰 후에 기존 방법을 최대한 활용하여 새로운 Asymmetric Gradient Guidance (AGG)를 제시하였다.
1. Gradient guidance: a review
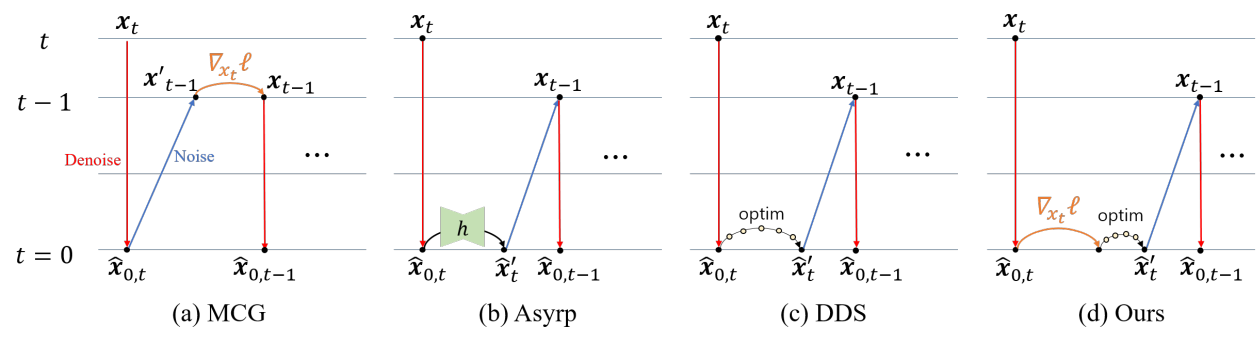
Manifold Constraint Gradient (MCG)
MCG는 Tweedie 공식을 사용하여 noisy한 이미지 $x_t$를 추정된 깨끗한 이미지 \(\hat{x}_{0,t}\)에 투영하는 것으로 시작한다. 구체적으로, 샘플링은 다음과 같이 $x_{t-1}$을 가이드하는 것을 포함한다.
\[\begin{equation} x'_{t-1} \leftarrow x_{t-1} - \nabla_{x_t} \ell (\hat{x}_{0,t} (x_t)) \end{equation}\]여기서 $x_t$는 초기에 얻은 다음 step의 샘플이다. 기울기 값은 $x_t$에 대해 denoise된 이미지 \(\hat{x}_{0,t}\)로 계산된 loss $\ell$의 기울기이다. MGC 기울기는 원래 noisy한 매니폴드에 유지되도록 업데이트를 시행한다.
Asymmetric Reverse Sampling (Asyrp)
Asyrp은 reverse sampling step을 다음과 같이 바꾼다.
\[\begin{equation} x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \hat{x}_{0,t} (\tilde{\epsilon}_\theta (x_t, t)) + D_t (\epsilon_\theta (x_t, t)) + \sigma_t z_t \\ \textrm{where} \quad \tilde{\epsilon}_\theta (x_t, t) = \epsilon_\theta (x_t, t) + \Delta \epsilon_t \end{equation}\]Diffusion model의 업데이트 $\Delta \epsilon_t$를 계산하기 위해 score 네트워크 $\epsilon_\theta$의 bottleneck feature를 조작하는 $h$-space 개념을 도입했다. 따라서 위 식에서 \(\hat{x}_{0,t} (\tilde{\epsilon}_\theta)\)를 \(\hat{x}_{0,t} (\epsilon_\theta (x_t \vert \Delta h_t, t))\)로 설정하며, 이는 조작된 $h$-space를 사용하는 score network에서 추정된 깨끗한 이미지이다.
Decomposed Diffusion Sampling (DDS)
DDS에서는 Tweedie 공식을 통해 깨끗한 매니폴드에 샘플을 project한 후 다음과 같은 최적화 문제를 해결한다.
\[\begin{equation} \Delta x_0 = \underset{\Delta}{\arg \min} \ell (\hat{x}_{0,t} + \Delta) \end{equation}\]다음은 수정된 reverse sampling step이다.
\[\begin{equation} x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} (\hat{x}_{0,t} (\epsilon_\theta (x_t, t)) + \Delta x_0) + D_t (\epsilon_\theta (x_t, t)) + \sigma_t z_t \end{equation}\]일부 정규 조건 (regularity condition) 하에서 conjugate gradient (CG) 기반 업데이트 $\Delta x_0$는 여전히 업데이트된 샘플 \(\hat{x}_{0,t} + \Delta x_0\)가 깨끗한 매니폴드에 머물도록 보장하므로 후속 noising process가 샘플을 올바른 noisy한 매니폴드로 전송한다.
2. Asymmetric Gradient Guidance
Key observation
앞서 언급한 접근 방식들이 겉보기에는 달라 보이지만 근본적인 연관성이 있다. 구체적으로, $\Delta x$를 $x_t$의 noisy한 데이터 space로 다시 변환함으로써 원래 forward model
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon_t \end{equation}\]가 다음과 같이 변환될 수 있다.
\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} (\hat{x}_{0,t} + \Delta x_0) + \sqrt{1 - \bar{\alpha}_t} \tilde{\epsilon}_t \\ \textrm{where} \quad \tilde{\epsilon}_t := \epsilon_t - \sqrt{\frac{\bar{\alpha}_t}{1 - \bar{\alpha}_t}} \Delta x_0 \end{equation}\]따라서 Asyrp에 의한 diffusion model 업데이트와 DDS에 의한 샘플 도메인 업데이트는 scaling factor까지 동일하다. 또한 변분법을 이용하면 $\Delta x_0$는
\[\begin{equation} \Delta x_0 = − \eta \nabla_{x_t} \ell (\hat{x}_{0,t} (x_t)) \end{equation}\]로 나타낼 수 있으며, 어떤 $s_t$에 대해
\[\begin{equation} \tilde{\epsilon}_t := \epsilon_t + s_t \nabla_{x_t} \ell (\hat{x}_{0,t} (x_t)) \end{equation}\]가 되며, diffusion model의 조건 기반 guidance를 제안한다. 이전 연구에서는 $s_t = \sqrt{1 - \bar{\alpha}_t}$로 설정하였다.
Proposed method
샘플 업데이트와 diffusion model 업데이트 간의 동등성을 고려할 때 조건부 diffusion에 대한 일반적인 업데이트 공식을 도출할 수 있다.
\[\begin{equation} x_{t-1} = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \hat{x}'_t + D_t (\epsilon_\theta (x_t, t)) + \sigma_t z_t \end{equation}\]여기서 다음 두 가지 형식의 \(\hat{x}'_t\)가 대해 상호 교환적으로 사용된다.
\[\begin{equation} \hat{x}'_t = \begin{cases} \hat{x}_{0,t} (\epsilon_t) - \nabla_{x_t} \ell (\hat{x}_{0,t} (x_t)) \\ \hat{x}_{0,t} (\tilde{\epsilon}_t), \quad \textrm{where} \quad \tilde{\epsilon}_t := \epsilon_t - s_t \nabla_{x_t} \ell (\hat{x}_{0,t} (\epsilon_t)) \end{cases} \end{equation}\]따라서 남은 문제는 역전파가 필요한 MCG 기울기 \(\nabla_{x_t} \ell (\hat{x}_{0,t} (x_t))\)의 계산이다. DDS의 핵심 아이디어는 일반적인 linear inverse problem의 경우 기본 solution space가 Kyrov subspace에 있을 때 denoise된 샘플에서 시작하는 몇 step의 표준 CG 업데이트를 통해 업데이트 샘플이 여전히 깨끗한 매니폴드에 존재하도록 보장한다는 것이다. 따라서 MGC에 대한 계산 비용이 많이 드는 역전파를 우회할 수 있다.
불행하게도 DDS 접근법은 loss function이 관심 있는 텍스트 중심 및 이미지 중심 image translation에서 비롯된 경우 관련 inverse problem을 linear inverse problem으로 나타낼 수 없기 때문에 안정적인 해를 제공하지 않는다. 그러나 각 iteration에서 MCG를 적용하는 것은 계산 비용이 많이 든다. 이 문제를 해결하기 위해 저자들은 다음과 같은 \(\hat{x}'_t\)의 하이브리드 업데이트를 제안하였다.
\[\begin{equation} \hat{x}'_t = \bar{x}'_t + \underset{\Delta}{\arg \min} \ell (\bar{x}'_t + \Delta), \\ \textrm{where} \quad \bar{x}'_t := \hat{x}_{0,t} (\tilde{\epsilon}_t) \end{equation}\]여기서 첫 번째 항의 loss 최소화는 Adam optimizer를 사용하여 MGC 기울기 없이 수행되며, \(\tilde{\epsilon}_t\)는
\[\begin{equation} \tilde{\epsilon}_t := \epsilon_t - s_t \nabla_{x_t} \ell (\hat{x}_{0,t} (\epsilon_t)) \end{equation}\]로 계산된다. 이는 image translation task의 경우 업데이트된 샘플이 올바른 매니폴드에 존재하도록 연속적인 DDS 최적화에 한 step의 MGC 기울기가 필요함을 의미한다. 이를 Asymmetric Gradient Guidance (AGG)라고 한다.
AGG는 이미지 diffusion model뿐만 아니라 latent diffusion model (LDM)에도 적용할 수 있다. 이 경우 이미지 diffusion에 $x_t$를 사용하는 대신 인코더 뒤에 내장된 latent $z_t$를 사용한다.
3. Loss function
Image translation을 위해 loss function은 이미지 도메인 변경을 위한 스타일 loss \(\ell_\textrm{sty}\)와 원본 이미지 구조를 유지하기 위한 정규화 loss \(\ell_\textrm{reg}\)의 두 부분으로 구성된다.
\[\begin{equation} \ell_\textrm{total} = \lambda_\textrm{sty} \ell_\textrm{sty} + \lambda_\textrm{reg} \ell_\textrm{reg} \end{equation}\]제어 파라미터 \(\lambda_\textrm{reg}\)로 콘텐츠 보존 강도를 제어할 수 있다.
\(\ell_\textrm{sty}\)는 DiffuseIT에서 사용하는 스타일 loss function을 활용한다. 구체적으로, text-guided I2I의 경우 사전 학습된 CLIP 모델을 사용하여 임베딩 유사성 loss를 사용하는 반면 image-guided I2I의 경우 DINO ViT를 사용하는 토큰 매칭 loss를 사용한다.
구조적 보존을 위해 DiffuseIT는 ViT를 사용하여 강력한 콘텐츠 보존 loss를 활용한다. 그러나 저자들은 더 간단하면서도 더 효율적인 정규화 접근법을 제안하였다. 구체적으로 DDIM forward process에서 미리 계산된 중간 샘플을 사용한 reverse step의 정규화 방식을 제안하였다.
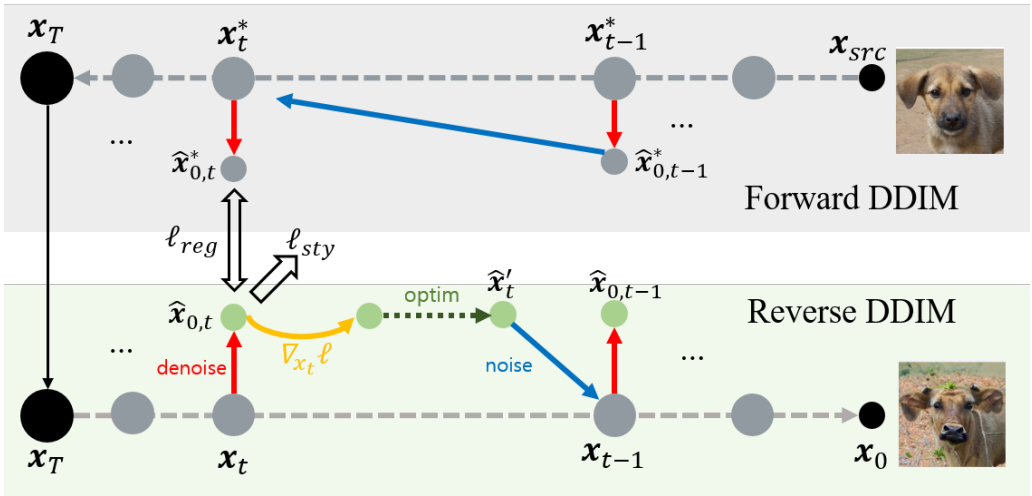
위 그림에서 볼 수 있듯이 DDIM의 forward sampling에서는 reverse sampling을 수정하여 deterministic하게 중간 샘플을 계산할 수 있다. 다음과 같이 timestep $t$를 변경하고 $\sigma_t = 0$으로 설정한다.
여기서 $x_t^\ast$는 소스 이미지 \(x_\textrm{src}\)에서 계산된 noisy한 이미지이고 \(\hat{x}_{0,t}^\ast (\epsilon_t)\)는 Tweedie 공식을 사용하여 계산된 denoise된 이미지다. 또한 모든 $t$에 대해 \(\hat{x}_{0,t}^\ast (\epsilon_t)\)를 저장하는 대신 \(T − t_\textrm{edit} < t\)에 대해서만 저장한다. 여기서 \(t_\textrm{edit}\)는 gradient guidance를 중지하는 지점이다. 저장된 중간 샘플을 사용한 정규화 loss는 다음과 같이 정의된다.
\[\begin{equation} \ell_\textrm{reg} = d (\hat{x}_{0,t}^\ast (\epsilon_t^{\theta_\ast}), \hat{x}_{0,t} (\epsilon_t^\theta)) \end{equation}\]여기서 $d(\cdot, \cdot)$은 $l_1$ loss를 사용한다.
정규화에는 두 가지 주요 효과가 있다.
- 상당한 편차를 방지하여 소스 이미지의 속성을 따르도록 출력을 안내하는 일반적인 효과를 제공한다.
- Guidance 타겟도 특정 timestep $t$에서 denoise된 이미지이기 때문에 조작된 깨끗한 이미지 \(\hat{x}'_t\)가 원래 매니폴드에서 벗어나는 것을 방지하는 데 도움이 된다. 이 제약은 생성 출력의 품질 향상으로 이어진다.
Experimental Results
- 구현 디테일
- DiffuseIT의 공식 소스코드 참조
- ImageNet 256$\times$256에서 사전 학습된 unconditional score model 사용
- Diffusion step: $T = 60$, \(t_\textrm{edit} = 20\)
- 생성 프로세스는 1개의 RTX 3090에서 15초 소요
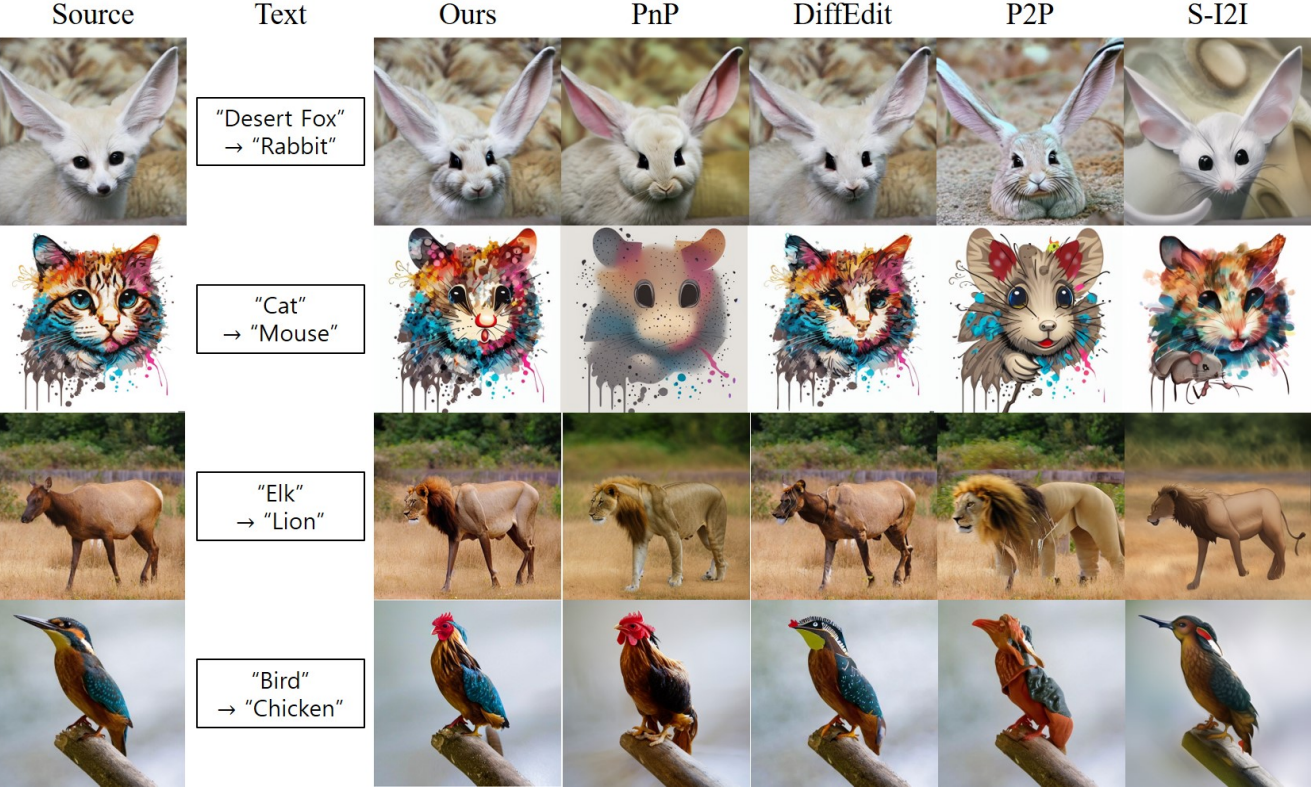
1. Text-guided Image Translation
다음은 text-guided image translation 결과를 정성적으로 비교한 것이다.

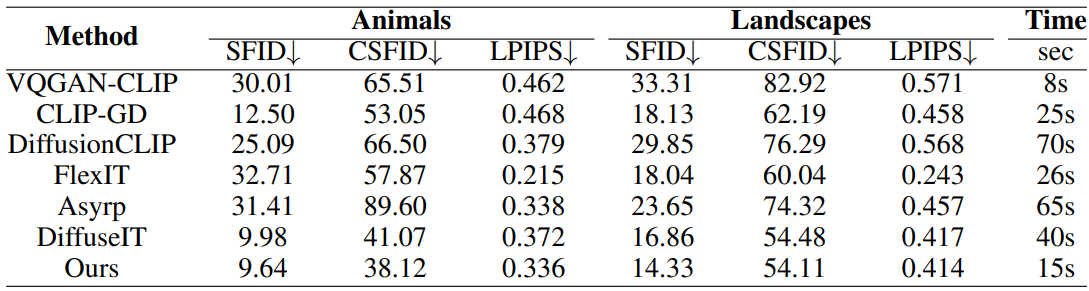
다음은 text-guided image translation 결과를 정량적으로 비교한 표이다.
2. Image-guided Image Translation
다음은 image-guided image translation 결과를 정성적으로 비교한 것이다.

3. Experiment on Latent Diffusion Models
다음은 LDM을 사용한 text-guided image translation 결과를 정성적으로 비교한 것이다.
4. Other applications
다음은 다양한 애플리케이션의 예시들이다.

Limitations

사전 학습된 CLIP 모델을 사용하기 때문에 위 그림과 같이 텍스트 조건이 CLIP space에서 원본 이미지와 거리가 먼 경우 (ex. 사자 $\rightarrow$ 건물) 문제가 있다.