[논문리뷰] ADIR: Adaptive Diffusion for Image Reconstruction

arXiv 2022. [Paper] [Page]
Shady Abu-Hussein, Tom Tirer, Raja Giryes
Tel Aviv University | Bar-Ilan University
6 Dec 2022

Introduction

이미지 복원 문제는 열화된 이미지 $y \in \mathcal{R}^{m}$이 주어지면 처음 보는 깨끗한 이미지 $x \in \mathbb{R}^n$로 복원하는 문제이다. 다양한 열화 세팅은 다음과 같은 선형 관측 모델로 표현할 수 있다.

\[\begin{equation} y = Ax + e \\ A \in \mathbb{R}^{m \times n}, \quad e \in \mathbb{R}^m \sim \mathcal{N} (0, \sigma^2 I_m) \end{equation}\]

$A$는 measurement operator이고 $e$는 measurement noise이다. 일반적으로 위의 관측 모델을 피팅하는 것만으로는 $x$를 성공적으로 복원하는 데 충분하지 않다. 따라서 $x$의 특성에 대한 사전 지식이 필요하다.

본 논문에서는 Adaptive Diffusion framework for Image Reconstruction (ADIR)을 제안한다. 먼저, $x$의 복원을 사전 학습된 diffusion model의 범위로 제한하면서 inverse problem을 해결하는 diffused guidance sampling 방법을 고안한다. 본 논문의 방법은 Deep mean-shift priors for image restoration 논문에 사용된 guidance에 대한 새로운 수정 사항을 기반으로 한다.

그런 다음 $y$를 사용하여 알 수 없는 $x$를 복구하는 데 유용한 패턴에 diffusion model을 적용하는 두 가지 기술을 제안한다. 모델의 parameter를 조정하는 것은 $y$의 열화에 민감하지 않은 embedding space에서 $y$와 유사한 외부 이미지 $K$개 또는 $y$에 직접 기반한다. 이러한 이미지는 다양한 데이터셋에서 검색할 수 있으며 CLIP과 같은 인코더 모델을 사용하여 계산할 수 있다.

ADIR 프레임워크는 inverse problem에 대한 최초의 적응 diffusion 방식이다. 두 가지 state-of-the-art diffusion model인 Stable Diffusion과 Guided Diffusion에 본 논문의 방법을 적용하여 평가하고, super-resolution과 deblurring task에서 기존 방법보다 성능이 우수함을 보여준다. 마지막으로 제안한 적응 전략이 텍스트 기반 이미지 편집에도 사용될 수 있음을 보여준다.

Method

1. Denoising Diffusion Models

(DDPM 논문리뷰 참고)

2. Diffusion based Image Reconstruction

이미지 복원을 위해 Diffusion models beat GANs on image synthesis 논문의 guidance 방법을 확장한다. 먼저, 저자들은 프레임워크를 inverse problem으로 개념적으로 일반화한다. 즉, $y$가 주어지면 특정 클래스의 임의 샘플이 아닌 $y$와 관련된 $x$를 생성하기 위해 guide된 reverse diffusion process를 수정한다. 이상적으로는 $t$ iteration에서의 guide 방향은 likelihood 함수 $p_{y \vert x}$의 기울기를 따라야 한다.

해당 논문과 본 논문의 핵심 차이점은 classifier가 아닌 특정 열화 이미지 $y$에 기반해야 한다는 것이다. 그러나 likelihood 함수 $p_{y \vert x_0}$만 알기 때문에 깨끗한 이미지에 대해서만 사용할 수 있다. 이 문제를 극복하기 위하여 저자들은 중간 likelihood 함수 $p_{y \vert x_t}$를 사용한다.

Log-likelihood gradient를 사용하여 diffusion 과정을 guide한다. 사후 확률

\[\begin{equation} p_\theta (x_t \vert x_{t-1}, y) \propto p_\theta (x_t \vert x_{t-1}) p_{y \vert x} (y \vert x_t) \end{equation}\]

에서 샘플링하는 것이 목표이며, $p_\theta (x_t \vert x_{t-1}) = \mathcal{N}(\mu_\theta, \Sigma_\theta)$이다.

$\log p_{y \vert x_t} (y \vert \cdot)$이 $\Sigma_\theta^{-1}$보다 낮은 곡률을 가진다고 가정하면 $x_t = \mu_\theta$ 주변에서 다음과 같은 테일러 전개가 성립한다.

\[\begin{aligned} \log p_{y \vert x_t} (y \vert x_t) & \approx \log p_{y \vert x_t} (y \vert x_t) |_{x_t = \mu_\theta} \\ & + (x_t - \mu_\theta)^T \nabla_{x_t} \log p_{y \vert x_t} (y \vert x_t) |_{x_t = \mu_\theta} \\ & = (x_t - \mu_\theta)^T g + C_1 \end{aligned}\]

$g$는 log-likelihood 함수의 기울기이고, $C_1$은 $x_t$에 의존하지 않는 상수이다. 그런 다음 위 식을 사용하여 사후 확률을 표현하면 다음과 같다.

\[\begin{equation} \log (p_\theta (x_t \vert x_{t-1}) p_{y \vert x_t} (y \vert x_t)) \approx C_2 + \log p(z) \\ z \sim \mathcal{N}(\mu_\theta + \Sigma_\theta g, \Sigma_\theta) \end{equation}\]

$C_2$는 $x_t$에 의존하지 않는 상수이다. 따라서 reverse rpocess를 $y$로 컨디셔닝하기 위해서는 $g$를 각 $t$에서 알아야 한다.

$t = 0$에서 정확한 log-likelihood 함수를 알고 있다. Noise $e$가 $\sigma^2$을 분산으로 하는 Gaussian noise이므로, 아래와 같은 분포를 가진다.

\[\begin{equation} p_{y \vert x} (y \vert x) = \mathcal{N} (Ax, \sigma^2 I_m) \propto e^{-\frac{1}{2\sigma^2} \| y - Ax \|_2^2} \end{equation}\]

$y$가 관찰 모델로 $x_0$와 관련되기 때문에 아래 식이 성립한다.

\[\begin{equation} \log p_{y \vert x_0} (y \vert x_0) \propto - \| Ax_0 - y \|_2^2 \end{equation}\]

그러나 likelihood 함수에 대한 tractable한 식이 없다. 따라서 위 식에서 영감을 받아 다음 근사식을 세울 수 있다.

\[\begin{equation} \log p_{y \vert x_t} (y \vert x_t) \approx \log p_{y \vert x_0} (y \vert \hat{x}_0 (x_t)) \\ \hat{x}_0 (x_t) := \frac{x_t - \sqrt{1 - \bar{\alpha}_t \epsilon_\theta (x_t, t)}}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \end{equation}\]

$g$를 각 iteration $t$에서 다음과 같이 근사할 수 있다.

\[\begin{equation} g \approx - \nabla_{x_t} \| A \hat{x}_0 (x_t) - y \|_2^2 |_{x_t = \mu_\theta} \end{equation}\]

다음 완화 식으로 안정성 문제를 극복할 수 있다. 사전 학습된 denoiser가 $x_t$로부터 예측한 $\epsilon_\theta$에 대하여 다음 식이 성립한다.

\[\begin{aligned} \|A \hat{x}_0 (x_t) - y \|_2^2 &= \|A \bigg( \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \epsilon_\theta}{\sqrt{\vphantom{1} \bar{\alpha}_t}} \bigg) - y \|_2^2 \\ & \approx \| A x_t - \sqrt{1 - \bar{\alpha}_t} A \epsilon_\theta - \sqrt{\vphantom{1} \bar{\alpha}_t} y \|_2^2 \\ & = \|A x_t - \sqrt{\vphantom{1} \bar{\alpha}_t} y - \sqrt{1 - \bar{\alpha}_t} A \epsilon_\theta \|_2^2 \\ & = \|A x_t - y_t \|_2^2 \end{aligned}\]

결과적으로 $g$의 식에 이를 대입하면 다음 식을 얻을 수 있다.

\[\begin{equation} g \approx -2 A^T (A x_t - y_t) |_{x_t = \mu_\theta} \end{equation}\]

위 식을 사용하여 Algorithm 1과 같이 사후 확률 분포를 샘플링할 수 있다.

3. Adaptive Diffusion

이미지 복원을 위한 guided inverse diffusion flow를 정의하였으므로, inverse problem에서 정의된 대로 주어진 diffusion model을 주어진 $y$에 어떻게 적용할 수 있는지를 논의해야 한다. 사전 학습된 모델을 $(\epsilon_\theta(\cdot), \Sigma_\theta (\cdot))$이라 가정하면, 적응 방식은 다음 최소화 문제로 정의된다.

\[\begin{equation} \hat{\theta} = \underset{\theta}{\arg \min} \sum_{t=1}^T l_\textrm{simple} (y, \epsilon_\theta) \end{equation}\]

위 식은 SGD를 사용하여 효율적으로 풀 수 있다.

Denoising network를 $y$에 적응시키기 위해서 이미지에서 반복되는 cross-scale feature들을 학습하도록 한다.

그러나 몇몇 경우에서는 반복되는 패턴에 대한 가정을 만족하지 않으므로 이 접근법은 학습된 sharpness를 잃을 수 있다. 따라서 본 논문에서는 few-shot finetuning adaptation을 확장하여 $y$ 대신 $x$와 비슷한 $K$개의 다양한 이미지를 큰 데이터셋에서 검색하는 알고리즘을 제안하며, 이 알고리즘은 기존 모델의 embedding distance를 사용한다.

$(\xi_v (\cdot), \xi_l (\cdot))$를 visual-language에 대해 학습된 off-the-shelf multi-modal encoder라고 하자 (ex. CLIIP, BLIP, CyCLIP). 크고 다양한 데이터셋이 주어지면 $K$개의 이미지 \(\{z_k\}_{k=1}^K\)를 검색한다. \(\mathcal{D}_{IA}\)를 임의의 외부 데이터셋이라고 하면 다음이 성립한다.

\[\begin{aligned} \{z_k\}_{k=1}^K = & \{z_1, \cdots, z_K \vert \phi_\xi (z_1, y) \le \cdots \le \phi_\xi (z_K, y) \\ & \le \phi_\xi (z, y), \forall z \in \mathcal{D}_{IA} \backslash \{z_1, \cdots, z_K\} \} \end{aligned}\]

$\phi_\xi (a,b) = 2 \arcsin (0.5 | \xi (a) - \xi (b) |_2)$는 공간적 거리이고 $\xi$는 비전 인코더나 언어 인코더이다.

$K$-NN 이미지 \(\{z_k\}_{k=1}^K\)를 \(\mathcal{D}_{IA}\)에서 검색한 후, diffusion model을 finetuning하여 $y$의 컨텍스트가 denoising network에 적응시킨다. 이 K-NN 기반의 적응 테크닉을 ADIR (Adaptive Diffusion for Image Reconstruction)이라 부르며, 아래 그림과 같다.

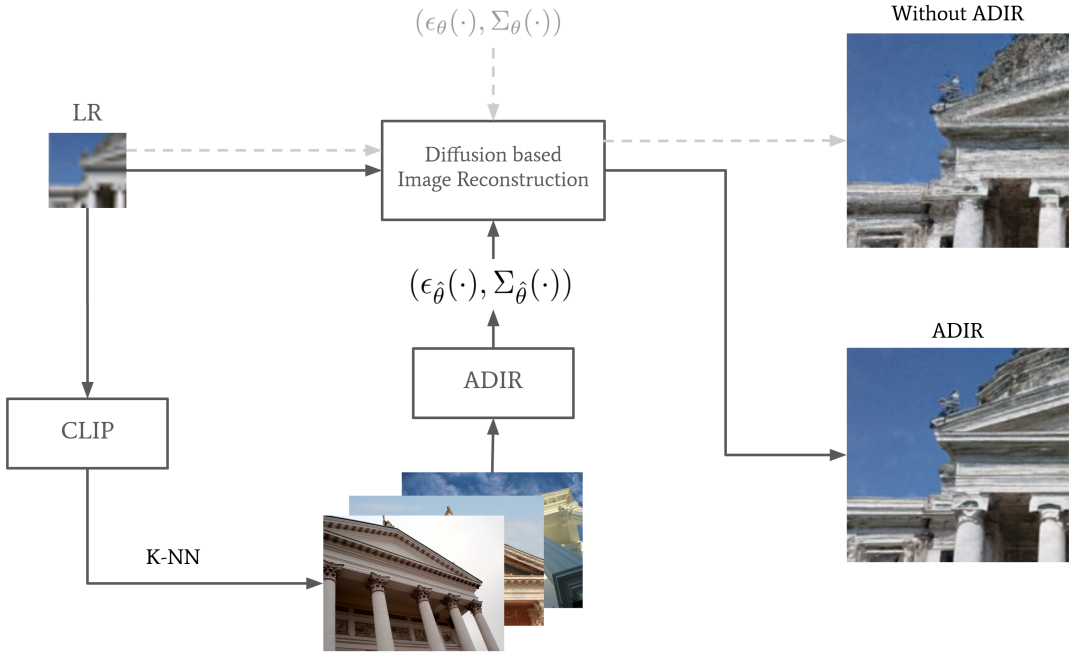
Experiments

본 논문의 방법을 Guided Diffusion (GD)과 Stable Diffusion (SD)에 적용한 후 평가하였다. \(\mathcal{D}_{IA}\)로 Google Open Dataset을 사용하였으며, D는 $K = 20$, SD는 $K = 50$으로 설정하였다.

구체적인 configuration은 아래 표와 같다.

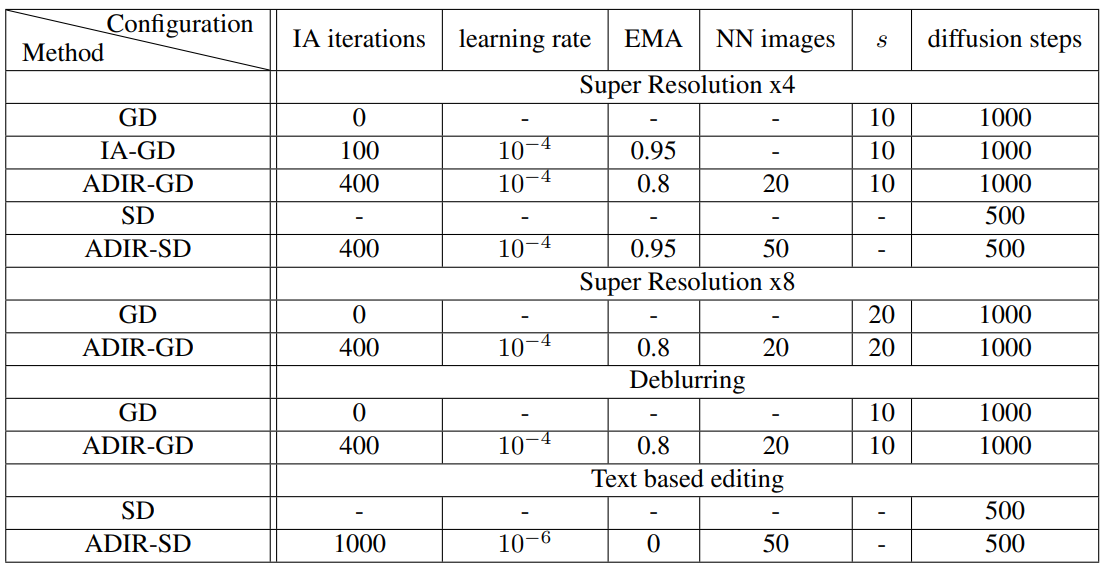
1. Super Resolution

다음은 unconditional guided diffusion model에 대하여 4배($128^2 \rightarrow 512^2$)로 super resolution한 결과이다. AVA-MUSIQ와 KonIQ-MUSIQ로 평가하였다. (높을수록 좋음)

다음은 Stable Diffusion SR model에 대하여 4배($256^2 \rightarrow 1024^2$)로 super resolution한 결과의 샘플과 AVA-MUSIQ, KonIQ-MUSIQ 지표이다.

2. Deblurring

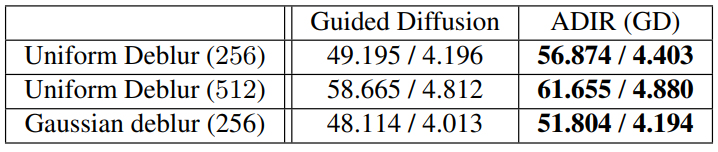
다음은 unconditional guided diffusion model에 대하여 5$\times$5 box filter와 $\sigma = 10$으로 deblurring한 결과의 샘플과 AVA-MUSIQ, KonIQ-MUSIQ 지표이다.

3. Text-Guided Editing

다음은 텍스트 기반 이미지 편집 결과를 비교한 것이다.