[논문리뷰] AdaptDiffuser: Diffusion Models as Adaptive Self-evolving Planners

ICML 2023 (Oral). [Paper] [Page] [Github]
Zhixuan Liang, Yao Mu, Mingyu Ding, Fei Ni, Masayoshi Tomizuka, Ping Luo
Department of Computer Science, The University of Hong Kong | UC Berkeley | College of Intelligence and Computing, Tianjin University
3 Feb 2023

Introduction

오프라인 강화 학습(RL)은 실제 환경과 상호 작용하지 않고 이전에 수집된 오프라인 데이터에서 정책을 학습하는 것을 목표로 한다. 기존의 오프라인 RL 접근 방식에는 value function 피팅 또는 policy gradient 계산이 필요하며, 이는 제한된 오프라인 데이터로 인해 얻기 어렵다.

생성 시퀀스 모델링의 최근 발전은 state, action, reward, value 시퀀스의 공동 분포를 모델링하여 기존 RL 문제에 대한 효과적인 대안을 제공한다. 예를 들어 Decision Transformer는 오프라인 RL을 조건부 시퀀스 모델링의 한 형태로 캐스팅하여 temporal difference learning과 같은 기존 RL 알고리즘을 통해 정책을 학습할 필요 없이 보다 효율적이고 안정적인 학습이 가능하다. RL을 시퀀스 모델링 문제로 취급함으로써 long-term credit 할당을 위한 bootstrapping의 필요성을 우회한다.

이를 위해 차세대 오프라인 RL을 위한 더 나은 시퀀스 모델링 알고리즘을 고안하는 것이 필수적이다. Diffusion probability model은 자연어 처리 및 컴퓨터 비전을 위한 생성 시퀀스 모델링에서 성공이 입증되었으므로 이러한 시도에 이상적이다. 또한 planning 및 의사결정을 위한 패러다임으로서의 잠재력을 보여준다. 예를 들어 diffusion 기반 planning 방법은 오프라인 데이터를 기반으로 궤적 trajectory diffusion model을 학습시키고 샘플링 중에 reward guidance를 통해 생성된 궤적에 유연한 제약을 적용한다. 결과적으로 diffusion planner는 long horizon task에서 Decision Transformer나 Trajectory Transformer와 같은 Transformer 기반 planner에 비해 눈에 띄는 성능 우위를 보이며 동시에 reward 최대화 제어가 아닌 목표 컨디셔닝 제어를 가능하게 한다.

Diffusion planner는 특정 영역에서 성공을 거두었지만 학습 데이터의 다양성 부족으로 인해 성능이 제한된다. 의사결정 task에서 다양한 오프라인 학습 데이터셋을 수집하는 비용이 높을 수 있으며 이러한 충분하지 않은 다양성은 환경 및 행동 policy의 역학을 정확하게 캡처하는 diffusion model의 능력을 방해한다. 결과적으로 diffusion model은 전문가 데이터가 충분하지 않거나 특히 새로운 task에 직면했을 때 성능이 떨어지는 경향이 있다. 이는 강력한 생성 시퀀스 모델링 능력이 있는 diffusion model 자체를 개선하기 위해 diffusion model에서 생성된 합성 데이터를 사용할 수 있는지 질문을 제기하게 한다. Diffusion model의 self-evolution이 가능하면 더 강력한 planner가 되어 잠재적으로 더 많은 의사결정 요구 사항과 downstream task에 도움이 될 수 있다.

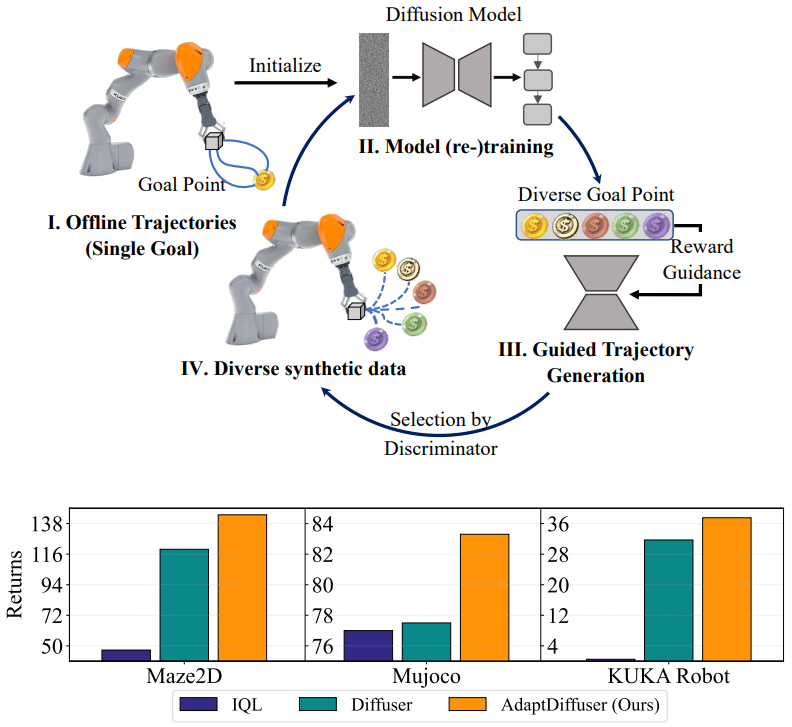
본 논문에서는 self-evolution을 통해 새로운 설정 및 시나리오로 일반화할 수 있는 목표 컨디셔닝 task를 위한 diffusion 기반 planner인 AdaptDiffuser를 제시한다 (위 그림 참고). 특정 전문가 데이터에 크게 의존하는 기존 접근 방식과 달리 AdaptDiffuser는 reward gradient를 guidance로 사용하여 기존 task와 보지 못한 task 모두에 대한 풍부하고 다양한 합성 데모 데이터를 생성한다. 그런 다음 생성된 데모 데이터는 discriminator에 의해 필터링되며, 여기서 이러한 고품질 데이터는 diffusion model을 finetuning하는 데 사용되므로 이전에 본 task에 대한 자체 bootstrapping 능력이 크게 개선되고 새로운 task를 일반화하는 일반화하는 능력이 향상된다. 결과적으로 AdaptDiffuser는 기존 벤치마크에서 diffusion 기반 planner의 성능을 향상시킬 뿐만 아니라 추가 전문가 데이터 없이도 보지 못한 task에 적응할 수 있다.

Preliminary

강화 학습은 일반적으로 $\mathcal{M} = (\mathcal{S}, \mathcal{A}, \mathcal{T}, \mathcal{R}, \gamma)$로 표시되는 완전히 관찰 가능한 state space가 있는 MDP(Markov Decision Process)로 모델링된다. 여기서 $\mathcal{S}$는 state space고 $\mathcal{A}$는 action space이다. $\mathcal{T}$는 state transition function으로, state $s_t \in \mathcal{S}$에서 주어진 action $a_t \in \mathcal{A}$에 대하여 $s_{t+1} = \mathcal{T} (s_t, a_t)$이다. $\mathcal{R}(s_t, a_t)$는 reward function이며 $\gamma \in (0,1]$은 미래의 reward를 위한 discount factor이다.

오프라인 강화학습을 시퀀스 모델링 task로 생각하면, 궤적 최적화의 목적은 return의 기대값을 최대화하는 action 최적 시퀀스 $a_{0:T}^\ast$를 찾는 것이며, reward의 기대값은 $\mathcal{R}(s_t, a_t)$의 합이다.

\[\begin{equation} a_{0:T}^\ast = \underset{a_{0:T}}{\arg \max} \mathcal{J} (s_0, a_{0:T}) = \underset{a_{0:T}}{\arg \max} \sum_{t=0}^T \gamma^t R (s_t, a_t) \end{equation}\]

Diffusion model을 활용한 시퀀스 데이터 생성 방법은 생성 프로세스가 반복적인 denoising 과정 $p_\theta (\tau^{i-1} \vert \tau^i)$이며, $\tau$는 시퀀스고 $i$는 diffusion timestep이다.

그런 다음 시퀀스 데이터의 분포는 denoising process의 step-wise 조건부 확률로 확장된다.

\[\begin{equation} p_\theta (\tau^0) = \int p (\tau^N) \prod_{i=1}^N p_\theta (\tau^{i-1} \vert \tau^i) d \tau^{1:N} \end{equation}\]

여기서 $p (\tau^N)$은 표준 정규 분포이고 $\tau^0$는 원래의 시퀀스 데이터를 나타낸다.

Diffusion model의 파라미터 $\theta$는 $p_\theta (\tau^0)$의 negative log-likelihood의 evidence lower bound (ELBO)를 최소화하여 최적화된다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} - \mathbb{E}_{\tau^0} [\log p_\theta (\tau^0)] \end{equation}\]

Denoising process는 입력 데이터에 noise를 추가해 손상시키는 forward diffusion process $q(\tau^i \vert \tau^{i-1})$의 reverse이다. Forward process가 정규 분포를 따르고 분산이 충분히 작으면 reverse process는 가우시안으로 parameterize할 수 있다.

\[\begin{equation} p_\theta (\tau^{i-1} \vert \tau^i) = \mathcal{N} (\tau^{i-1} \vert \mu_\theta (\tau^i, i), \Sigma^i) \end{equation}\]

모델의 학습의 경우, 다음과 같은 간단화된 loss가 사용된다.

\[\begin{equation} \mathcal{L}_\textrm{denoise} (\theta) := \mathbb{E}_{i, \tau^0 \sim q, \epsilon \sim \mathcal{N}(0, I)} [\| \epsilon - \epsilon_\theta (\tau^i, i) \|^2] \end{equation}\]

$\tau^i$는 궤적 $\tau^0$를 $i$번 $\epsilon$으로 손상시킨 것이다. $\epsilon_\theta (\tau^i, i)$를 $\mu_\theta (\tau^i, i)$로 매핑하는 함수가 closed-form이므로 이 loss는 $p_\theta (\tau^{i-1} \vert \tau^i)$의 평균 $\mu_\theta$를 예측하는 것과 동등하다.

Method

1. Planning with Task-oriented Diffusion Model

Diffuser 논문을 따라, 본 논문은 planning 궤적을 다음과 같은 state의 추가 차원으로 action을 포함하는 특수한 종류의 시퀀스 데이터로 재정의할 수 있다.

\[\begin{equation} \tau = \begin{bmatrix} s_0 & s_1 & \cdots & s_T \\ a_0 & a_1 & \cdots & a_T \end{bmatrix} \end{equation}\]

그런 다음 diffusion probabilistic model을 사용하여 궤적 생성을 수행할 수 있다. 그러나 planning의 목적은 원래 궤적을 복원하는 것이 아니라 가장 높은 reward로 미래의 action을 예측하는 것이므로 이미지 합성에서 큰 성공을 거둔 guided diffusion model을 사용하여 조건부 생성 문제로 오프라인 강화 학습을 공식화해야 한다. 따라서 다음과 같은 조건부 diffusion process를 구동한다.

\[\begin{equation} q(\tau^{i+1} \vert \tau^i), \quad p_\theta (\tau^{i-1} \vert \tau^i, y(\tau)) \end{equation}\]

여기서 새로운 항 $y(\tau)$는 reward-to-go $\mathcal{J}(\tau^0)$와 같은 주어진 궤적 $\tau$의 특정 정보이며, 궤적 등에 의해 충족되어야 하는 제약 조건이다. 이를 기반으로 목적 함수를 다음과 같이 쓸 수 있다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \min} - \mathbb{E}_{\tau^0} [\log p_\theta (\tau^0 \vert y(\tau^0))] \end{equation}\]

따라서, reward-to-go를 최대화하는 것이 목표인 task의 경우 \(\mathcal{O}_t\)로 timestep $t$에서의 궤적의 최적성을 나타낸다. 그리고 \(\mathcal{O}_t\)는 \(p(\mathcal{O}_t = 1) = \exp (\gamma^t \mathcal{R}(s_t, a_t))\)인 베르누이 분포를 따른다. \(p(\mathcal{O}_{1:T} \vert \tau^i)\)가 특정 Lipschitz 조건을 만족하면, reverse diffusion process의 조건부 transition 확률은 다음과 같이 근사될 수 있다.

\[\begin{equation} p_\theta (\tau^{i-1} \vert \tau^i, \mathcal{O}_{1:T}) \approx \mathcal{N}(\tau^{i-1}; \mu_\theta + \alpha \Sigma g, \Sigma) \end{equation}\]

여기서 $g$는

\[\begin{aligned} g &= \nabla_\tau \log p (\mathcal{O}_{1:T} \vert \tau) |_{\tau = \mu_\theta} \\ &= \sum_{t=0}^T \gamma^t \nabla_{s_t, a_t} \mathcal{R} (s_t, a_t) |_{(s_t, a_t) = \mu_t} \\ &= \nabla_\tau \mathcal{J} (\mu_\theta) \end{aligned}\]

단일 지점 조건부 제약 조건을 만족하는 것이 목표인 task의 경우, 모든 diffusion timestep의 샘플링된 값을 조건부 값으로 대체하여 제약 조건을 단순화할 수 있다.

이 패러다임은 diffusion model을 기반으로 하지 않는 이전의 planning 방법과 비슷한 결과를 얻었지만 reverse diffusion process에서 조건부 guidance만 수행하고 forward process에서 unconditional diffusion model이 완벽하게 학습되었다고 가정한다.

그러나 생성된 궤적 $\tau$의 품질은 guide된 기울기 $g$뿐만 아니라 학습된 평균 $\mu_\theta$ 및 unconditional diffusion model의 공분산 $\Sigma$에 더 많이 의존한다. 학습된 $\mu_\theta$가 최적의 궤적에서 멀리 벗어나면 guidance $g$가 아무리 강하더라도 최종 생성된 결과는 매우 편향되고 품질이 낮을 것이다. 그런 다음 \(\mathcal{L}_\textrm{denoise}\)로 학습하면 \(\mu_\theta\)의 품질은 학습 데이터에 달려 있지만 보지 못한 task에서 품질이 고르지 않다. 기존의 diffusion 기반 planning 방법은 기존 task와 보지 못한 task 모두에서 이러한 성능을 제한하는 문제를 해결하지 못하여 적응 능력이 낮다.

2. Self-evolved Planning with Diffusion

따라서, 이러한 planner의 적응 능력을 향상시키기 위해 diffusion model을 기반으로 한 새로운 스스로 진화된 의사결정 접근 방식인 AdaptDiffuser를 제안하여 forward diffusion process의 학습된 평균 $\mu_\theta$ 및 공분산 $\Sigma$의 품질을 향상시킨다. AdaptDiffuser는 스스로 진화된 합성 데이터 생성을 사용하여 $\tau_0$으로 표시된 학습 데이터셋을 강화하고 이러한 합성 데이터를 fine-tuning하여 성능을 향상시킨다. 그 후 AdaptDiffuser는 reward gradient의 guidance를 기반으로 주어진 task에 대한 최적의 action 시퀀스를 찾는다.

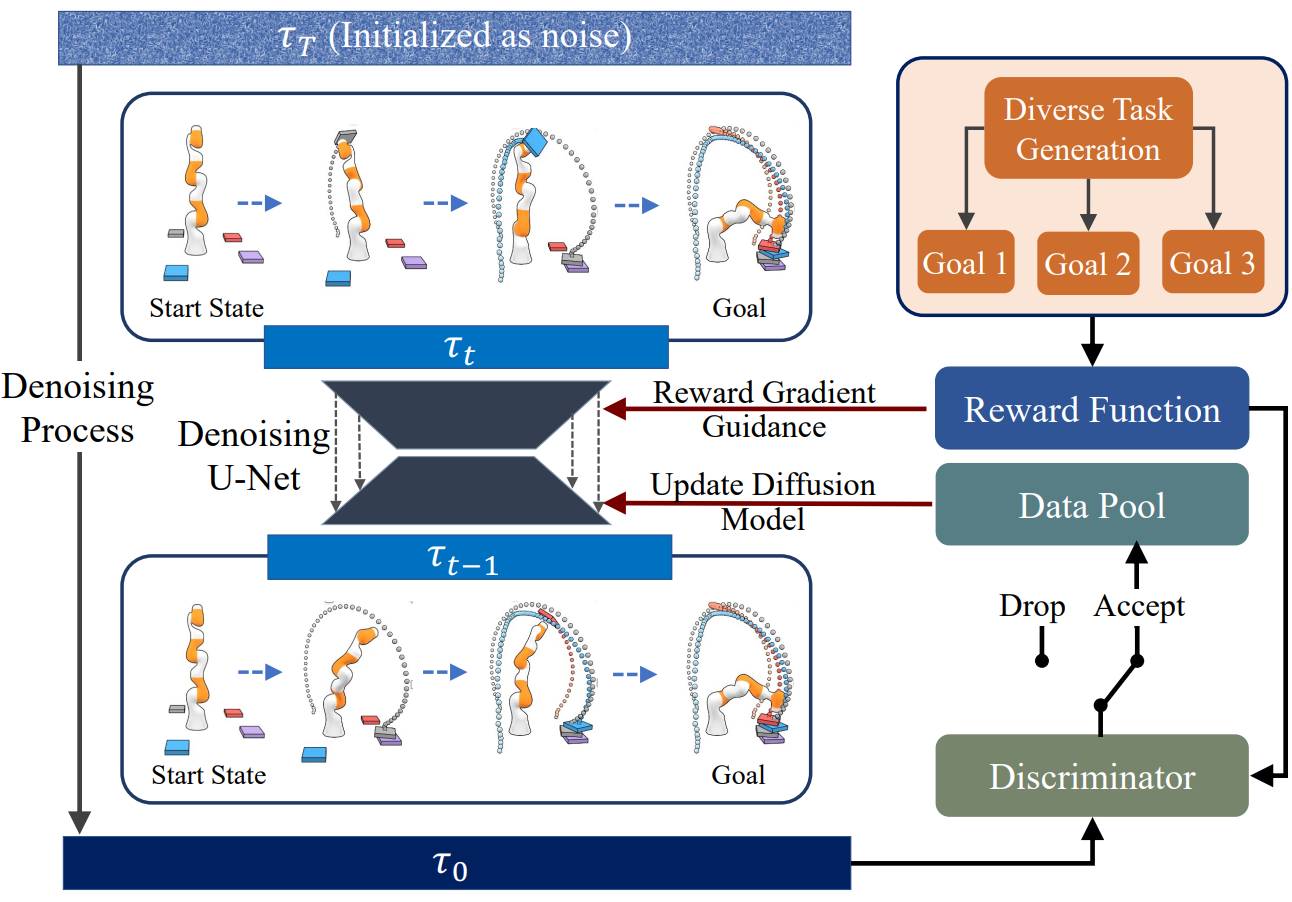
위 그림에서 볼 수 있듯이 AdaptDiffuser를 구현하기 위해 먼저 학습 데이터셋에 존재하지 않지만 실제 세계에서 diffusion model이 접할 수 있는 광범위한 시나리오 및 동작을 시뮬레이션하는 보지 못한 task에 대한 많은 수의 합성 데모 데이터를 생성한다. 이 합성 데이터는 원래의 diffusion model $\theta_0^\ast$의 샘플링 과정을 reward guidance와 함께 반복적으로 생성하여 생성 능력이 뛰어나다.

둘째, 생성된 데이터 풀에서 고품질 데이터를 선택하기 위해 reward guidance와 역학 일관성으로 정의된 discriminator $\mathcal{D}$를 사용한다. Diffusion model에 의해 denoise된 action 시퀀스 a의 역학 일관성을 측정하기 위해 state와 action과 동시에 $\mathcal{R}(s, a)$를 예측하는 이전 시퀀스 모델링 접근 방식과 다른 방식을 채택한다. 구체적으로, 생성된 궤적의 state 시퀀스 $s = [s_0, s_1, \cdots, s_T]$만 취한 다음 $\tilde{a}$로 표시된 실제 실행 가능한 action을 도출하기 위해 기존 controller를 사용하는 state tracking control를 수행한다. 예를 들어, Maze2D task의 경우 PID controller를 사용한다. 그런 다음 $\tilde{s}_0 = s_0$라고 하면

\[\begin{equation} \tilde{a}_t = \textrm{PID}(\tilde{s}_t, s_{t+1}), \quad \tilde{s}_{t+1} = \mathcal{T} (\tilde{s}_t, \tilde{a}_t) \end{equation}\]

가 된다. 먼저 controller를 사용하여 실행 가능한 action \(\tilde{a}_t\)를 계산한 다음 \(\tilde{a}_t\)를 수행하여 수정된 next state \(\tilde{s}_{t+1}\)을 얻는다. 그 후, 생성된 궤적에서 업데이트된 state \(\tilde{s}_{t+1}\)과 state $s_{t+2}$를 사용하여 다음 라운드를 진행한다. 또한 새로운 action $\tilde{a}$와 state $\tilde{s}$를 사용하여 수정된 reward $\tilde{R}(s, a) = R(\tilde{s}, \tilde{a})$를 계산한다. 수정된 reward를 사용하여 고품질 데이터 선택을 수행함으로써 역학 일관성에 대한 고려를 reward guidance에 대한 고려와 동일시하여 discriminator의 두 가지 목표를 통합할 수 있다.

마지막으로 선택된 궤적은 전문가 데이터 집합에 합성 전문가 데이터로 추가되고 diffusion model을 fine-tuning하는 데 사용돤다. 모델의 성능을 지속적으로 개선하고 새로운 task에 적응시켜 궁극적으로 일반화 성능을 향상시키기 위해 이 프로세스를 여러번 반복한다. 따라서 다음과 같이 공식화할 수 있다.

\[\begin{equation} \theta_k^\ast = \underset{\theta}{\arg \min} - \mathbb{E}_{\hat{\tau}_k} [\log p_\theta (\hat{\tau}_k \vert y(\hat{\tau}_k))] \\ \tau_{k+1} = \mathcal{G} (\mu_{\theta_k^\ast}, \Sigma, \nabla_\tau \mathcal{J} (\mu_{\theta_k^\ast})) \\ \hat{\tau}_{k+1} = [\hat{\tau}_k, \mathcal{D}(\tilde{R}(\tau_{k+1}))] \end{equation}\]

\(k \in \{0, 1, \cdots \}\)는 반복 라운드 수이고 초기 데이터셋은 $\hat{\tau}_0 = \tau_0$이다.

3. Reward-guided Synthetic Data Generatio

보지 못한 task에 대한 성능과 적응 능력을 개선하기 위해 현재 iteration에서 학습된 diffusion model을 사용하여 합성 궤적 데이터를 생성해야 한다. 저자들은 다양한 목표와 reward function을 갖는 일련의 task를 정의하여 이를 달성하였다.

Continuous Reward Function

MuJoCo로 표현되는 연속적인 reward function이 있는 task의 경우, reward 최대화 문제를 연속적인 최적화 문제로 변환하기 위해 연속 값에서 매핑된 확률로 최적성을 나타내는 이진 확률 변수를 정의하는 설정을 따른다.

Sparse Reward Function

Maze2D와 같은 목표 컨디셔닝 문제로 대표되는 task의 reward function은 생성된 궤적이 goal state $s_g$를 포함하는 경우에만 값이 1인 unit step function $\mathcal{J}(\tau) = \chi_{s_g} (\tau)$이다. 이 reward function의 기울기는 Dirac delta function으로 guidance로 사용할 수 없다. 그러나 극한을 취한다는 관점에서 본다면 해당하는 모든 샘플링된 값을 diffusion timestep에 대한 제약 조건으로 대체하여 제약 조건을 단순화할 수 있다.

Combination

많은 현실적인 task에는 이러한 두 종류의 reward function이 동시에 필요하다. 예를 들어 Maze2D 환경에 planner가 시작점에서 목표점까지 길을 찾는 것뿐만 아니라 미로에서 금화를 모으는 보조 task가 있는 경우가 있다고 해보자. 이 task는 생성된 궤적이 추가 reward point $s_c$를 통과해야 하는 timestep에 대해 모르기 때문에 sparse reward 항에 이 제약 조건을 추가하는 것이 불가능하다. 저자들은 해결책으로 이러한 두 종류의 방법을 보조 reward guiding function과 결합하여 제약 조건을 충족할 것을 제안한다.

\[\begin{equation} \mathcal{J}(\tau) = \sum_{t=0}^T \| s_t - s_c \|_p \end{equation}\]

그런 다음 위 식을 주변 확률 밀도 함수로 사용하여 생성된 궤적 $\tau^0$의 마지막 state가 $s_c$가 되도록 강제한다. Discriminator가 원하는 기준을 만족하는 생성된 궤적은 합성 전문가 데이터로 diffusion model 학습을 위한 학습 데이터셋에 추가된다. 충분한 양의 합성 데이터가 생성될 때까지 이 프로세스를 여러 번 반복한다. Return의 기대값과 dynamics transition 제약 조건의 guidance를 기반으로 고품질 데이터를 반복적으로 생성하고 선택함으로써 diffusion model의 성능과 적응성을 향상시킬 수 있다.

Experiment

1. Performance Enhancement on Existing Tasks

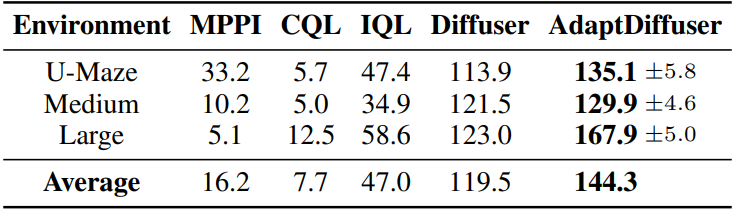
다음은 Maze2D 환경에서의 오프라인 강화 학습 성능을 나타낸 표이다.

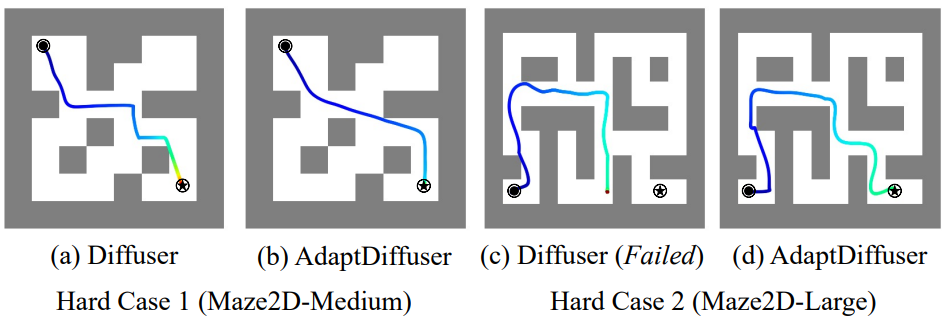
다음은 긴 planning 경로를 가진 Maze2D의 어려운 케이스들에서 AdaptDiffuser와 Diffuser를 비교한 것이다.

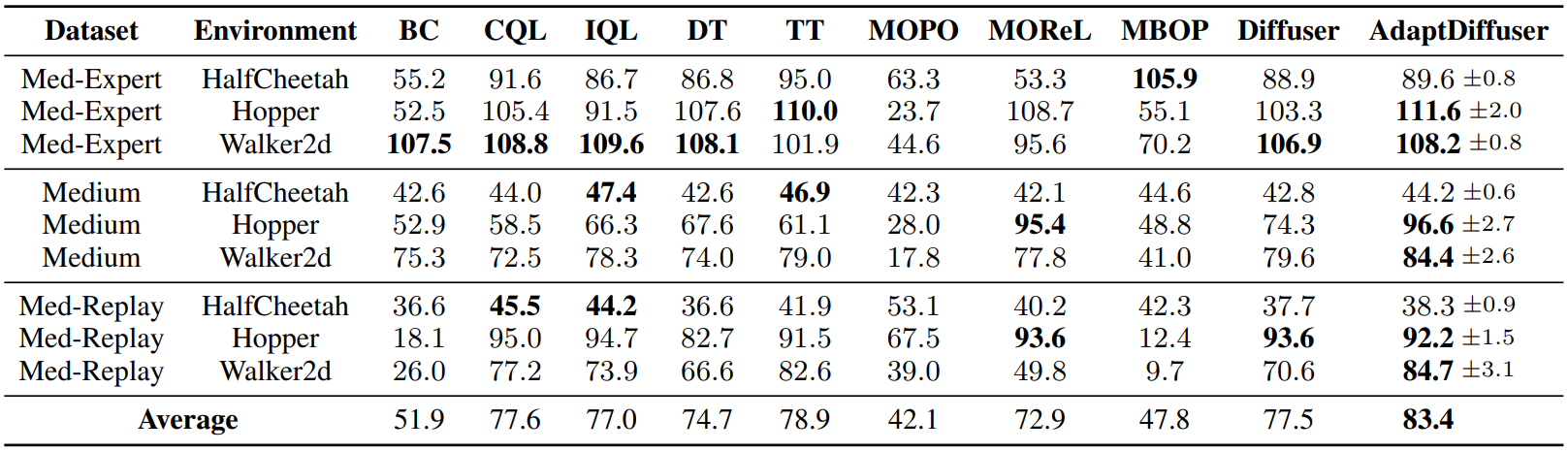
다음은 MuJoCo 환경에서의 오프라인 강화 학습 성능을 나타낸 표이다.

2. Adaptation Ability on Unseen Tasks

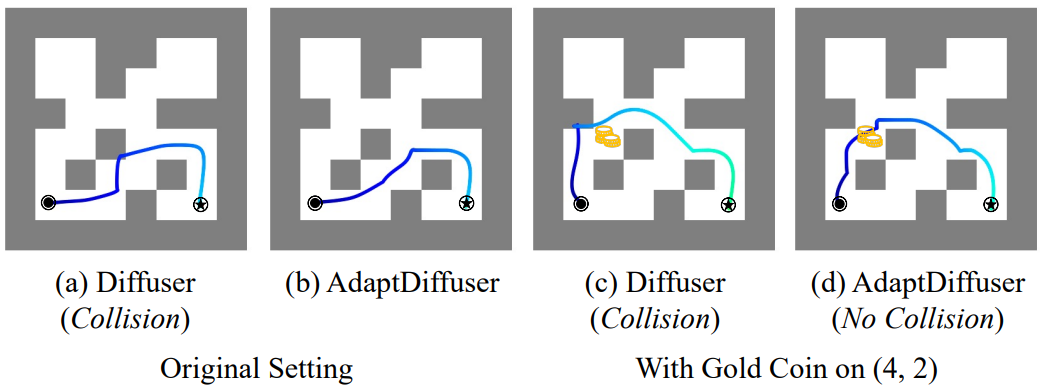
다음은 gold coin picking task에 대한 Maze2D 길찾기 결과를 비교한 것이다.

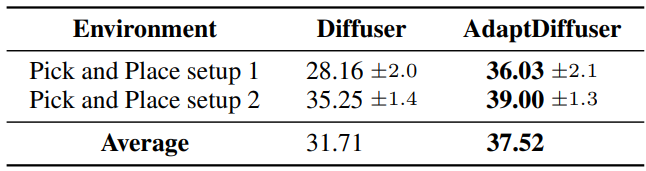
다음은 KUKA pick-and-place task에 대한 적응 성능을 비교한 표이다.

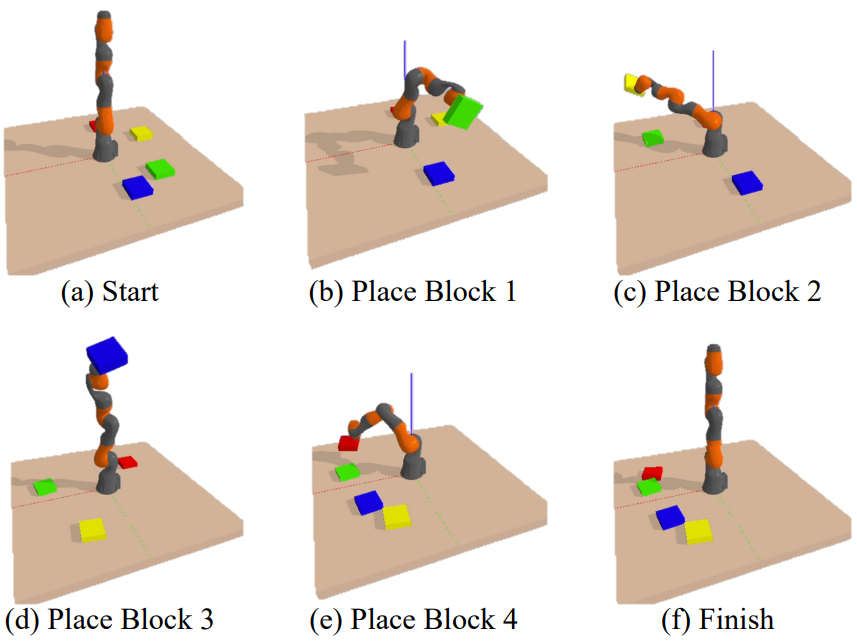
다음은 KUKA pick-and-place task에 대한 시각화이다.

3. Ablation Study

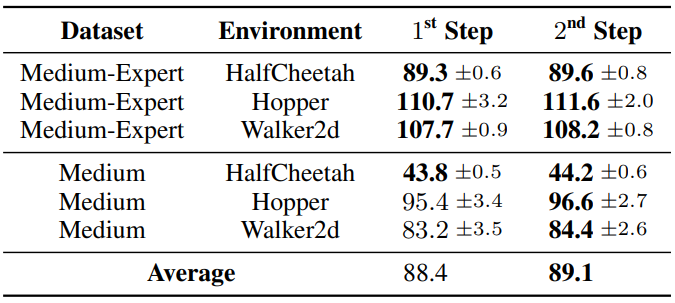
다음은 반복적인 step에 대한 ablation 결과를 나타낸 표이다. 3개의 랜덤 시드에 대한 평균과 분산을 계산한 것이다.

다음은 전문가 데이터의 양에 대한 ablation 결과를 나타낸 표이다.