[논문리뷰] 4D Gaussian Splatting for Real-Time Dynamic Scene Rendering
CVPR 2024. [Paper] [Page] [Github]
Guanjun Wu, Taoran Yi, Jiemin Fang, Lingxi Xie, Xiaopeng Zhang, Wei Wei, Wenyu Liu, Qi Tian, Xinggang Wang
HUST | Huawei Inc.
12 Oct 2023
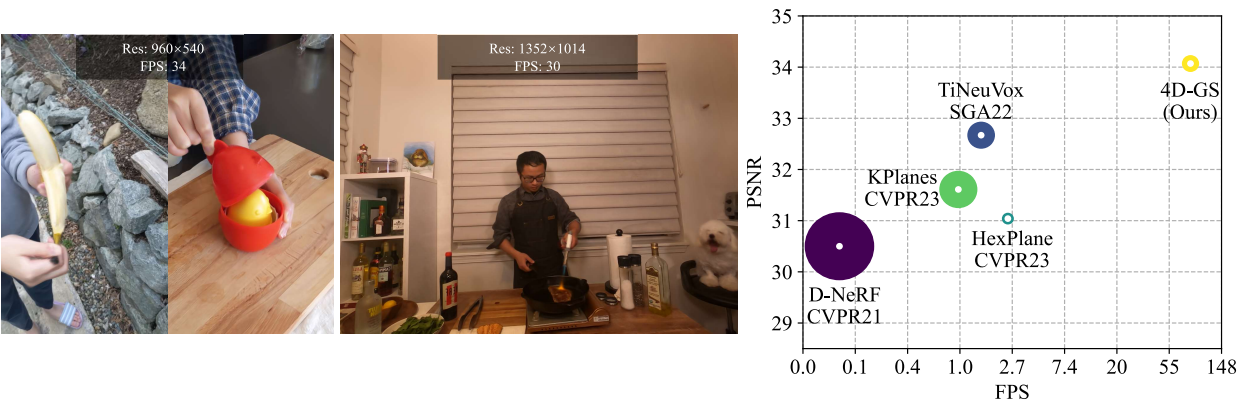
Introduction
Novel View Synthesis(NVS)는 3D 비전 도메인에서 중요한 task이며 많은 응용 분야에서 중요한 역할을 한다. NVS는 원하는 시점이나 장면의 타임스탬프에서 이미지를 렌더링하는 것을 목표로 하며 일반적으로 여러 2D 이미지에서 장면을 정확하게 모델링해야 한다. 동적 장면은 실제 시나리오에서 매우 일반적이며 렌더링은 중요하지만 시공간적으로 sparse한 입력을 사용하여 복잡한 동작을 모델링해야 하기 때문에 어렵다.
NeRF는 암시적 함수들을 사용하여 장면을 표현함으로써 새로운 뷰의 이미지를 합성하는 데 큰 성공을 거두었다. NeRF는 2D 이미지와 3D 장면을 연결하기 위해 볼륨 렌더링 기술을 도입하였다. 그러나 NeRF는 큰 학습 및 렌더링 비용을 발생하며, 일부 방법들에서 학습 시간을 며칠에서 몇 분으로 단축하였지만 렌더링 프로세스에는 여전히 무시할 수 없다.
최근 3D Gaussian Splatting(3D-GS)은 장면을 3D Gaussian으로 표현하여 렌더링 속도를 실시간 수준으로 크게 향상시켰다. 원래 NeRF의 번거로운 볼륨 렌더링은 3D Gaussian 포인트들 2D 평면에 직접 투영하는 효율적인 미분 가능한 splatting으로 대체되었다. 3D-GS는 실시간 렌더링 속도를 누릴 뿐만 아니라 장면을 보다 명시적으로 표현하므로 장면 표현을 더 쉽게 조작할 수 있다.
그러나 3D-GS는 정적인 장면에 중점을 둔다. 이를 4D 표현으로 동적 장면으로 확장하는 것은 합리적이고 중요하지만 어려운 주제이다. 핵심 과제는 sparse한 입력에서 복잡한 포인트들의 움직임을 모델링하는 것이다. 3D-GS는 점과 같은 Gaussian들로 장면을 표현함으로써 자연스러운 geometry prior를 유지한다. 직접적이고 효과적인 확장 접근 방식 중 하나는 각 타임스탬프에서 3D Gaussian들을 구성하는 것이지만 특히 긴 입력 시퀀스의 경우 저장/메모리 비용이 배가된다.
본 논문의 목표는 학습 및 렌더링 효율성을 모두 유지하면서 컴팩트한 표현인 4D Gaussian Splatting(4D-GS)을 구축하는 것이다. 이를 위해 spatial-temporal structure encoder와 매우 작은 multi-head Gaussian deformation decoder를 포함하는 효율적인 Gaussian deformation field network를 통해 Gaussian들의 움직임과 모양 변화를 표현한다. 3D Gaussian 집합은 하나만 유지된다. 각 타임스탬프에 대해 3D Gaussian들은 Gaussian deformation field에 의해 새로운 모양의 새로운 위치로 변환된다. 변환 과정은 Gaussian들의 움직임과 변형을 모두 나타낸다. 각 Gaussian의 움직임을 개별적으로 모델링하는 것과는 달리 spatial-temporal structure encoder는 인접한 서로 다른 3D Gaussian들을 연결하여 보다 정확한 움직임과 모양 변형을 예측할 수 있다. 그런 다음 변형된 3D Gaussian들을 타임스탬프 이미지에 따른 렌더링을 위해 직접 splatting할 수 있다.
Method
1. 4D Gaussian Splatting Framework
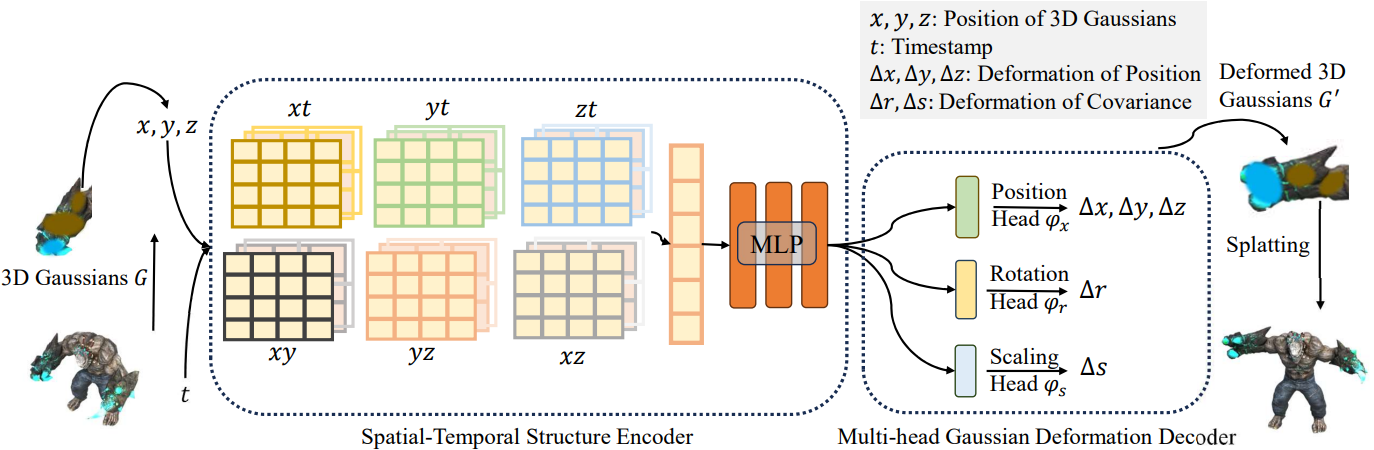
위 그림에서 볼 수 있듯이, view matrix $M = [R \vert T]$, 타임스탬프 $t$가 주어지면 4D Gaussian Splatting 프레임워크는 3D Gaussian $\mathcal{G}$와 Gaussian deformation field network $\mathcal{F}$를 포함한다. 그러면 새로운 뷰 이미지 $\hat{I}$는 미분 가능한 splatting $\mathcal{S}$에 의해 $\hat{I} = \mathcal{S}(M, \mathcal{G}^\prime)$로 렌더링된다. 여기서 $\mathcal{G}^\prime = \Delta \mathcal{G} + \mathcal{G}$이다.
구체적으로, 3D Gaussian의 변형 $\Delta \mathcal{G}$는 Gaussian deformation field network에 의해 도입되며
\[\begin{equation} \Delta \mathcal{G} = \mathcal{F}(\mathcal{G}, t) \end{equation}\]여기서 spatial-temporal structure encoder $\mathcal{H}$는 3D Gaussian들의 시간적 및 공간적 feature들을 모두 인코딩할 수 있다.
\[\begin{equation} f_d = \mathcal{H} (\mathcal{G}, t) \end{equation}\]그리고 multi-head Gaussian deformation decoder $\mathcal{D}$는 feature들을 디코딩하고 각 3D Gaussian의 변형 $\Delta \mathcal{G} = \mathcal{D}(f)$를 예측할 수 있으며, 그러면 변형된 3D Gaussian $\mathcal{G}^\prime$이 도입될 수 있다.
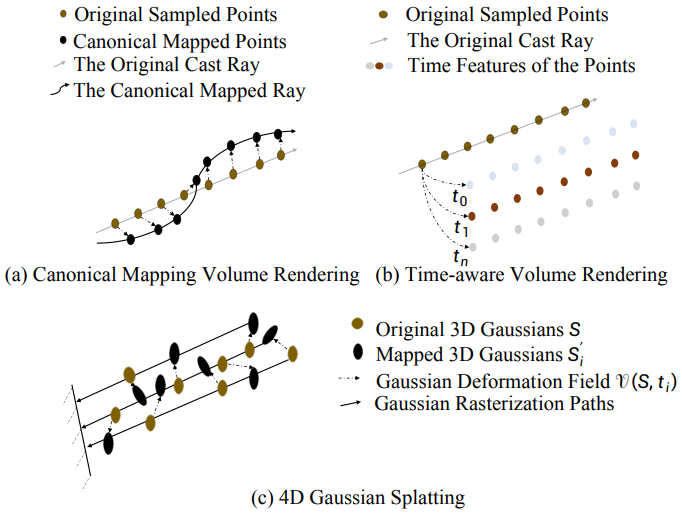
4D-GS의 렌더링 프로세스는 위 그림에 나와 있다. 4D-GS는 타임스탬프 $t$에 대하여 3D Gaussian $\mathcal{G}$를 다른 3D Gaussian의 그룹 $\mathcal{G}^\prime$으로 변환하여 미분 가능한 splatting의 효율성을 유지한다.
2. Gaussian Deformation Field Network
Gaussian deformation field를 학습하기 위한 네트워크는 효율적인 spatial-temporal structure encoder $\mathcal{H}$와 각 3D Gaussian의 변형을 예측하기 위한 Gaussian deformation decoder $\mathcal{D}$를 포함한다.
Spatial-Temporal Structure Encoder
근처의 3D Gaussian들은 항상 유사한 시공간적 정보를 공유한다. 저자들은 3D Gaussian의 feature들을 효과적으로 모델링하기 위해 multi-resolution HexPlane $R(i, j)$와 작은 MLP $\phi_d$를 포함하는 효율적인 spatial-temporal structure encoder $\mathcal{H}$를 도입하였다. 바닐라 4D 뉴럴 복셀은 메모리를 많이 사용하지만 4D K-Planes 모듈을 채택하여 4D 뉴럴 복셀을 6개 평면으로 분해한다. 특정 영역의 모든 3D Gaussian들은 bounding plane voxel에 포함될 수 있으며 Gaussian의 변형은 근처의 시간적 복셀에도 인코딩될 수 있다.
구체적으로, $\mathcal{H}$는 6개의 다중 해상도 평면 모듈 $R_l(i, j)$와 작은 MLP $\phi_d$를 포함한다.
\[\begin{equation} \mathcal{H} (\mathcal{G}, t) = \{ R_l (i,j), \phi_d \vert (i,j) \in \{(x,y), (x,z), (y,z), (x,t), (y,t), (z,t)\}, l \in \{1, 2\}\} \end{equation}\]위치 $\mathcal{X} = (x, y, z)$는 3D Gaussian들 $\mathcal{G}$의 평균값이다. 각 복셀 모듈은 $R(i, j) \in \mathbb{R}^{h \times lN_i \times lN_j}$로 정의된다. 여기서 $h$는 feature의 hidden 차원이고, $N$은 복셀 그리드의 기본 해상도, $l$은 업샘플링 스케일이다. 이는 시간적 정보를 고려하여 6개의 2D 복셀 평면 내에서 3D Gaussian들의 인코딩 정보를 수반한다. 개별 복셀 feature를 계산하는 식은 다음과 같다.
\[\begin{aligned} f_h &= \bigcup_l \prod \textrm{interp} (R_l (i,j)) \\ (i,j) &\in \{(x,y), (x,z), (y,z), (x,t), (y,t), (z,t)\} \end{aligned}\]$f_h \in \mathbb{R}^{h \times l}$은 뉴럴 복셀의 feature이다. interp는 그리드의 4개 정점에 위치한 복셀 feature를 쿼리하기 위한 bilinear interpolation이다. 그런 다음 작은 MLP $\phi_d$는 $f_d = \phi_d (f_h)$에 의해 모든 feature들을 병합한다.
Multi-head Gaussian Deformation Decoder
3D Gaussian들의 모든 feature들이 인코딩되면 multi-head Gaussian deformation decoder \(\mathcal{D} = \{\phi_x, \phi_r, \phi_s\}\)를 사용하여 원하는 변수를 계산할 수 있다. 별도의 MLP를 사용하여 위치 $\Delta \mathcal{X} = \phi_x (f_d)$, 회전 $\Delta r = \phi_r (f_d)$ 및 scaling $\Delta s = \phi_s (f_d)$의 변형을 계산한다. 그러면 변형된 feature $(\mathcal{X}^\prime, r^\prime, s^\prime)$은 다음과 같이 처리될 수 있다.
\[\begin{equation} (\mathcal{X}^\prime, r^\prime, s^\prime) = (\mathcal{X} + \Delta \mathcal{X}, r + \Delta r, s + \Delta s) \end{equation}\]최종적으로 변형된 3D Gaussian들 \(\mathcal{G}^\prime = \{\mathcal{X}^\prime, s^\prime, r^\prime, \sigma, \mathcal{C}\}\)를 얻는다.
3. Optimization
3D Gaussian Initialization
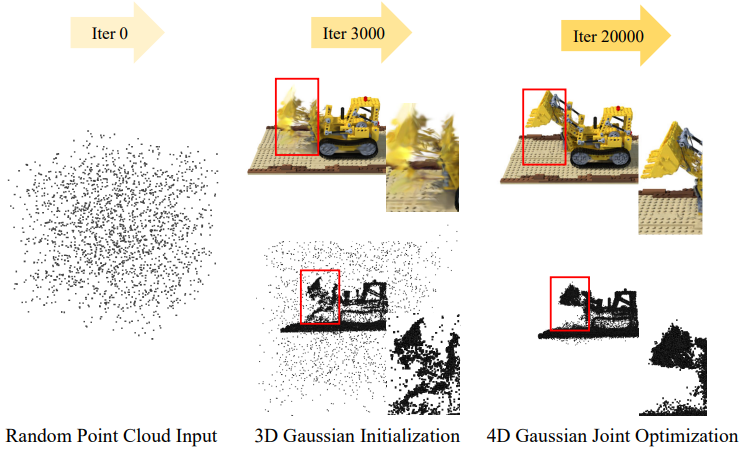
3D-GS는 3D Gaussian이 Structure from Motion(SfM) 포인트 초기화를 통해 잘 학습될 수 있음을 보여주었다. 마찬가지로, 4D Gaussian들도 적절한 3D Gaussian 초기화에서 fine-tuning되어야 한다. Warm-up을 위해 처음 3,000 iteration에서 3D Gaussian을 최적화한 다음 4D Gaussian $\hat{I} = \mathcal{s}(M, \mathcal{G}^\prime)$ 대신 3D Gaussian $\hat{I} = \mathcal{s}(M, \mathcal{G})$으로 이미지를 렌더링한다. 최적화 프로세스는 위 그림과 같다.
Loss Function
다른 재구성 방법들과 비슷하게 L1 color loss를 사용한다. 추가로 그리드 기반 total-variational loss \(\mathcal{L}_{tv}\)도 적용된다.
\[\begin{equation} \mathcal{L} = \hat{I} - I + \mathcal{L}_{tv} \end{equation}\]Experiment
- 데이터셋: D-NeRF, HyperNeRF, Neu3D
1. Results
다음은 합성 데이터셋(D-NeRF)에서 다른 방법들과 비교한 결과이다.
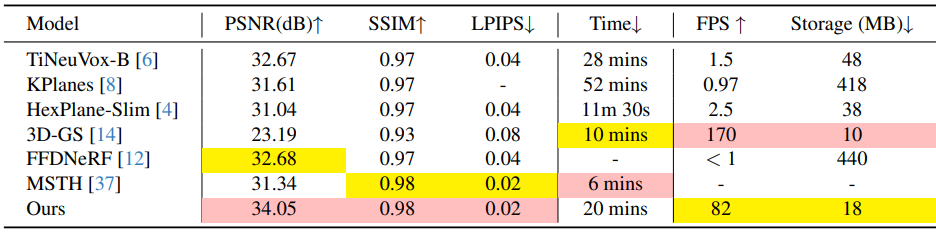

다음은 HyperNeRF에서 다른 방법들과 비교한 결과이다.
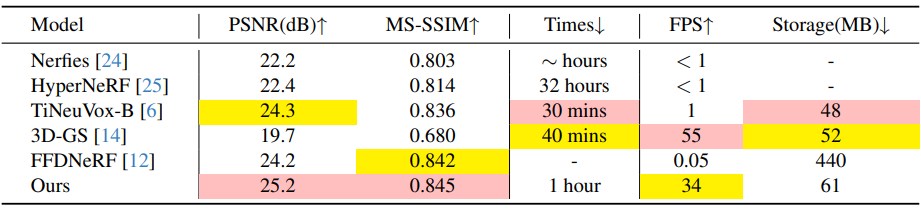

다음은 Neu3D에서 다른 방법들과 비교한 결과이다.
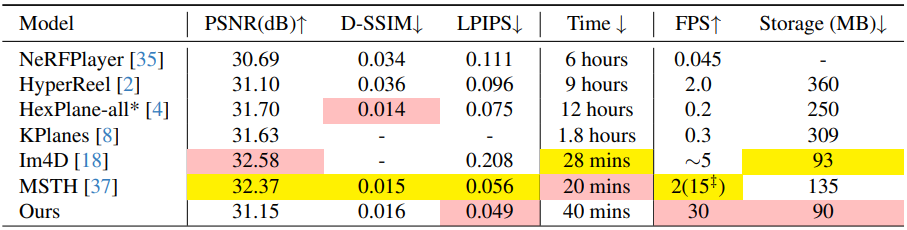
2. Ablation Study
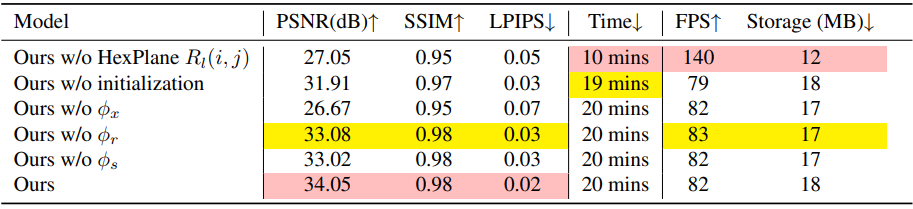
다음은 ablation study 결과이다. (D-NeRF)
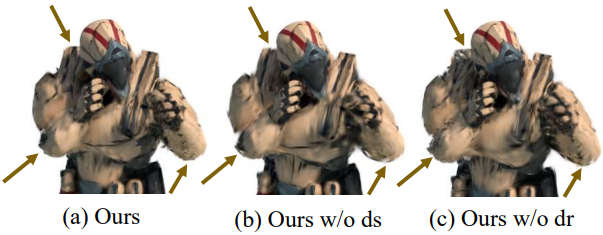
다음은 rotation decoder와 scaling decoder에 대한 ablation 결과이다.
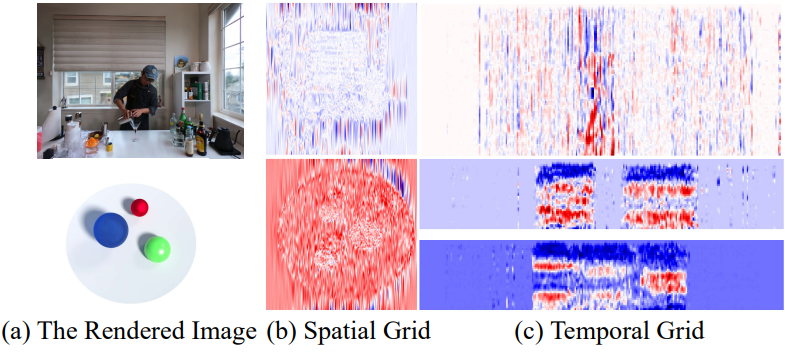
3. Discussions
다음은 HexPlane voxel grid를 시각화한 것이다.
다음은 3D Gaussian들을 이용하여 tracking을 시각화한 것이다.

다음은 서로 다른 4D Gaussian들을 합성한 예시이다.

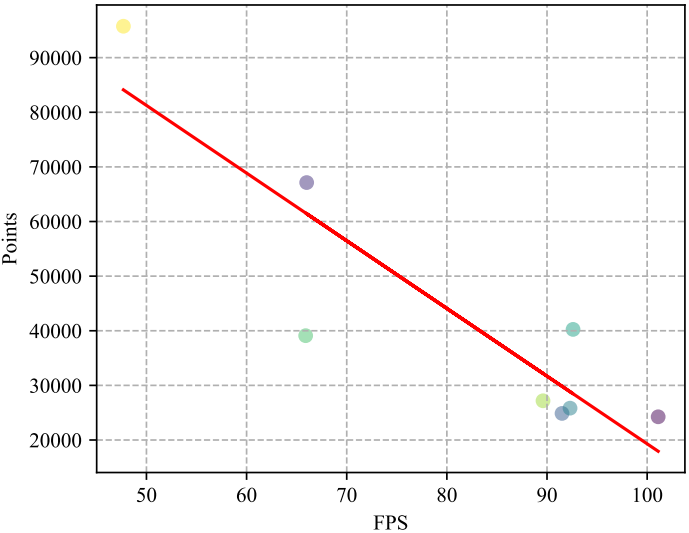
다음은 3D Gaussian 수에 따른 렌더링 속도를 나타낸 그래프이다.