[논문리뷰] Novel View Synthesis with Diffusion Models (3DiM)

arXiv 2023. [Paper] [Page]
Daniel Watson, William Chan, Ricardo Martin-Brualla, Jonathan Ho, Andrea Tagliasacchi, Mohammad Norouzi
Google Research
10 Apr 2023

Introduction

Diffusion model이라고도 하는 Diffusion Probabilistic Model (DPM)은 최근 강력한 생성 모델 계열로 부상하여 오디오 및 이미지 합성에서 state-of-the-art 성능을 달성하는 동시에 적대적 접근 방식보다 더 나은 학습 안정성을 보인다. Diffusion model은 다양한 image-to-image translation task에서 인상적인 경험적 결과를 달성했다.

Diffusion model이 연구되지 않은 image-to-image translation 문제 중 하나는 novel view synthesis이며, 주어진 3D 장면의 이미지 집합이 주어지면 장면이 새로운 시점에서 어떻게 보이는지 추론하는 것이다. 최근 Scene Representation Network(SRN)와 Neural Radiance Fields(NeRF)가 등장하기 전에 novel view synthesis에 대한 접근 방식은 일반적으로 생성 모델 또는 보간 또는 disparity 추정에 대한 보다 고전적인 기술을 기반으로 구축되었다. 오늘날 이러한 모델은 단일 기본 3D 표현(일명 “geometry-aware” model)의 볼륨 렌더링에 의해 이미지가 생성되기 때문에 3D 일관성이 보장되는 NeRF 클래스 모델보다 성능이 뛰어나다.

그러나 이러한 접근 방식에는 서로 다른 제한 사항이 있다. RegNeRF와 같이 적은 수의 이미지로 심하게 정규화된 NeRF는 매우 적은 수의 이미지가 주어질 때 원하지 않는 아티팩트를 생성하고, 여러 장면의 지식을 활용하지 못하며, 새로운 장면에 대한 하나 또는 아주 적은 view가 주어질 때 합리적인 모델은 장면의 가려진 부분을 완성하기 위해 extrapolate해야 한다. PixelNeRF와 VisionNeRF는 새로운 입력 view를 인코딩하는 feature map으로 컨디셔닝되는 NeRF 유사 모델을 학습시켜 이 문제를 해결한다. 그러나 이러한 접근 방식은 생성적이기보다는 퇴행적이며 결과적으로 다른 그럴듯한 모드를 생성할 수 없으며 흐려지는 경향이 있다. 이러한 유형의 실패는 이전에 회귀 기반 모델에서도 관찰되었다. CodeNeRF와 LoLNeRF와 같은 다른 연구들은 새로운 장면을 처리하기 위해 대신 test-time 최적화를 사용하지만 여전히 샘플 품질에 문제가 있다.

최근 Light Field Networks (LFN)과 Scene Representation Transformers (SRT)와 같은 geometry-free 접근 방식은 컨디셔닝 view 수가 제한된 few-shot 세팅에서 3D-aware 방법과 경쟁력 있는 결과를 달성했다. EG3D는 생성 모델을 활용하여 대략적인 3D 일관성을 제공한다. EG3D는 볼륨 렌더링과 함께 StyleGAN을 사용하고 생성적 super-resolution을 사용한다. 이 복잡한 설정과 비교하여 diffusion은 훨씬 간단한 아키텍처를 제공할 뿐만 아니라 튜닝하기 어려운 것으로 잘 알려진 GAN에 비해 더 간단한 hyper-parameter 튜닝이 가능하다. 특히, diffusion model은 이미 3D point cloud 생성에서 어느 정도 성공을 거두었다.

본 논문은 이러한 관찰과 image-to-image translation task에서 diffusion model의 성공에 동기를 부여하여 3D Diffusion Models (3DiM)을 도입한다. 3DiM은 동일한 장면의 이미지 쌍에 대해 학습된 image-to-image diffusion model로, 두 이미지의 포즈가 알려져 있다고 가정한다. Scene Representation Transformers에서 영감을 얻은 3DiM은 주어진 다른 view와 해당 포즈의 조건부 생성 모델을 구축하도록 학습되었다. 이 image-to-image model을 새로운 확률적 컨디셔닝 샘플링 알고리즘을 사용하는 autoregressive 생성을 통해 전체 3D 일관성을 가지는 프레임의 집합을 생성할 수 있는 모델로 전환할 수 있다. 이전 연구들과 비교하여 3DiM은 생성적 geometry-free model이며 학습을 많은 수의 장면으로 확장할 수 있게 하고 간단한 end-to-end 접근 방식을 제공한다.

Pose-Conditional Diffusion Models

3DiM에 동기를 부여하기 위해 확률론적 관점에서 소수의 이미지가 주어지는 novel view synthesis 문제를 고려해 보자. 3D 장면 $S$에 대한 완전한 설명이 주어지면 모든 포즈 $p$에 대해 포즈 $p$의 view $x(p)$는 $S$에서 완전히 결정된다. 즉, view는 주어진 $S$에 대해 조건부로 독립적이다. 그러나 view가 더 이상 조건부 독립이 아닌 $S$ 없이 $q(x_1, \cdots, x_m \vert x_{m+1}, \cdots, x_n)$ 형식의 분포를 모델링하는 데 관심이 있다.

구체적인 예는 다음과 같다. 사람의 머리 뒤쪽이 주어지면 정면에 대한 여러 개의 그럴듯한 view가 있다. 후면만 주어진 전면 view를 샘플링하는 image-to-image model은 특히 데이터 분포를 완벽하게 학습하는 경우 서로 일관성이 있다는 보장 없이 실제로 각 전면 view에 대해 서로 다른 출력을 생성해야 한다. 마찬가지로, 작게 보이는 물체의 view가 하나 주어지면 포즈 자체에 모호성이 있다.

물체가 작고 가까운가? 아니면 단순히 멀리 떨어져 있는가?

따라서 few-shot 세팅에 내재된 모호성을 고려할 때 생성된 view가 3D 일관성을 달성하기 위해 서로 의존할 수 있는 샘플링 체계가 필요하다. 이는 3D 표현 $S$가 주어지면 쿼리 광선이 조건부로 독립적인 NeRF 접근 방식과 대조된다. 이는 프레임 간에 조건부 독립성을 부과하는 것보다 훨씬 더 강력한 조건이다. NeRF 접근 방식은 단일 장면 $S$에 대해 가능한 가장 풍부한 표현을 학습하려고 시도하는 반면 3DiM은 $S$에 대한 생성 모델 학습의 어려움을 피한다.

1. Image-to-Image Diffusion Models with Pose Conditioning

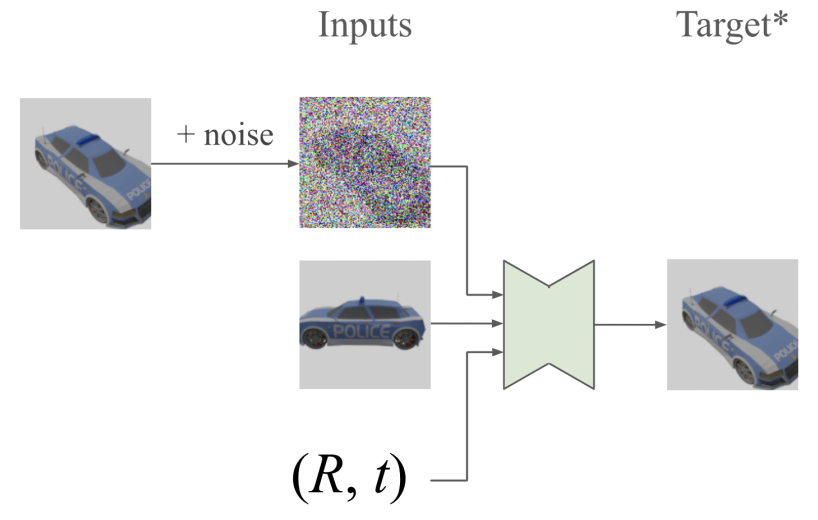
포즈 $p_1, p_2 \in \textrm{SE}(3)$에서 공통 장면의 view 쌍의 데이터 분포 $q(x_1, x_2)$가 주어지면, signal-to-noise-ratio (SNR) $\lambda$가 감소함에 따라 데이터 샘플에 점점 더 많은 양의 noise를 추가하는 Gaussian process를 정의한다.

\[\begin{equation} q (z_k^{(\lambda)} \vert x_k) := \mathcal{N} (z_k^{(\lambda)}; \sigma (\lambda)^{\frac{1}{2}} x_k, \sigma (-\lambda) I) \end{equation}\]

여기서 $\sigma (\cdot)$는 sigmoid function이다. Reparametrization trick을 적용하고 다음 식을 통해 이러한 주변 분포에서 샘플링할 수 있다.

\[\begin{equation} z_k^{(\lambda)} = \sigma (\lambda)^{\frac{1}{2}} x_k + \sigma (- \lambda)^{\frac{1}{2}} \epsilon, \quad \epsilon \sim \mathcal{N}(0,I) \end{equation}\]

그런 다음 한 쌍의 view가 주어지면 DDPM에서 제안한 목적 함수를 최소화하여 두 프레임 중 하나에서 이 프로세스를 reverse하는 방법을 배운다. 이는 ELBO를 최대화하는 것보다 훨씬 더 나은 샘플 품질을 생성하는 것으로 나타났다.

\[\begin{equation} L = \mathbb{E}_{q (x_1, x_2), \lambda, \epsilon} \| \epsilon_\theta (z_2^{(\lambda)}, x_1, \lambda, p_1, p_2) - \epsilon \|_2^2 \end{equation}\]

여기서 $\epsilon_\theta$는 다른 깨끗한 프레임 $x_1$이 주어졌을 때 프레임 $z_2^{(\lambda)}$를 denoise하는 신경망이다. $\lambda$는 log-SNR이다. 표기법을 더 읽기 쉽게 하기 위해 간단히 $\epsilon_\theta (z_2^{(\lambda)}, x_1)$이라고 쓴다.

2. 3D Consistency via Stochastic Conditioning

Motivation

이상적인 상황에서는 chain rule decomposition을 사용하여 3D 장면 프레임을 모델링한다.

\[\begin{equation} p(x) = \prod_i p(x_i \vert x_{<i}) \end{equation}\]

이 분해는 조건부 독립 가정 없이 분포를 정확하게 모델링하므로 이상적이다. 각 프레임은 모든 이전 프레임을 기준으로 autoregressive하게 생성된다. 그러나 저자들은 이 방법의 성능이 좋지 않음을 발견했다. 메모리 제한으로 인해 실제로는 제한된 수의 프레임으로만 컨디셔닝할 수 있다. 또한 입력 프레임 $k$의 최대 수를 늘릴수록 샘플 품질이 나빠지는 것을 발견했다. 가능한 최상의 샘플 품질을 달성하기 위해 $k = 2$ (즉, image-to-image model)를 선택한다. $k = 2$로 여전히 대략적인 3D 일관성을 달성할 수 있다. 프레임에 걸쳐 Markovian인 샘플러를 사용하는 대신 각 denoising step에서 컨디셔닝 프레임을 변경하여 diffusion sampling의 반복적 특성을 활용한다.

Stochastic Conditioning

일반적으로 $k = 1$ 또는 매우 작은 정적 장면의 컨디셔닝 view의 집합 \(X = \{x_1, \cdots, x_k\}\)로 시작한다. 그런 다음 step $\lambda_\textrm{min} = \lambda_T < \lambda_{T-1} < \cdots < \lambda_0 = \lambda_\textrm{max}$에 대한 denoising diffusion reverse process의 수정된 버전을 실행하여 새 프레임을 생성한다.

\[\begin{aligned} \hat{x}_{k+1} &= \frac{1}{\sigma (\lambda_t)^{\frac{1}{2}}} (z_{k+1}^{(\lambda_t)} - \sigma (- \lambda_t)^{\frac{1}{2}} \epsilon_\theta (z_{k+1}^{(\lambda_t)}, x_i)) \\ z_{k+1}^{(\lambda_{t-1})} &\sim q (z_{k+1}^{\lambda_{t-1}} \vert z_{k+1}^{(\lambda_t)}, \hat{x}_{k+1}) \end{aligned}\]

여기서 $i \sim \textrm{Uniform} ({1, \cdots, k})$는 각 denoising step에서 다시 샘플링한다. 즉, 각 개별 denoising step은 $\mathcal{X}$ (입력 view와 이전에 생성된 샘플을 포함하는 집합)의 다른 랜덤 view로 컨디셔닝된다. 이 샘플링 체인 실행을 마치고 최종 $x_{k+1}$을 생성하면 $\mathcal{X}$에 추가하고 더 많은 프레임을 샘플링하려면 이 절차를 반복한다. 충분한 denoising step이 주어지면 확률적 컨디셔닝을 통해 생성된 각 프레임이 모든 이전 프레임에 의해 guide될 수 있다.

실제로 256개의 denoising step을 사용하는데, 이는 높은 샘플 품질과 대략적인 3D 일관성을 모두 달성하기에 충분하다. 일반적으로 첫 번째 step(noise가 가장 많은 샘플)은 단순히 Gaussian, 즉 $z_i^{(\lambda_T)} \sim \mathcal{N}(0, I)$이고 마지막 step $\lambda_0$에서 노이즈 없이 샘플링한다.

Stochastic Conditioning은 실제로 잘 작동하는 실제 autoregressive 샘플링에 대한 naive한 근사치로 해석할 수 있다. 실제 autoregressive 샘플링에는 $\nabla_{z_{k+1}^{(\lambda)}} \log q (z_{k+1}^{(\lambda)} \vert x_1, \cdots, x_k)$ 형식의 score model이 필요하지만 이는 multi-view 학습 데이터가 엄격하게 필요하다. 궁극적으로 장면당 2개의 학습 view로 novel view synthesis을 가능하게 하는 것이 목표이다.

3. X-UNet

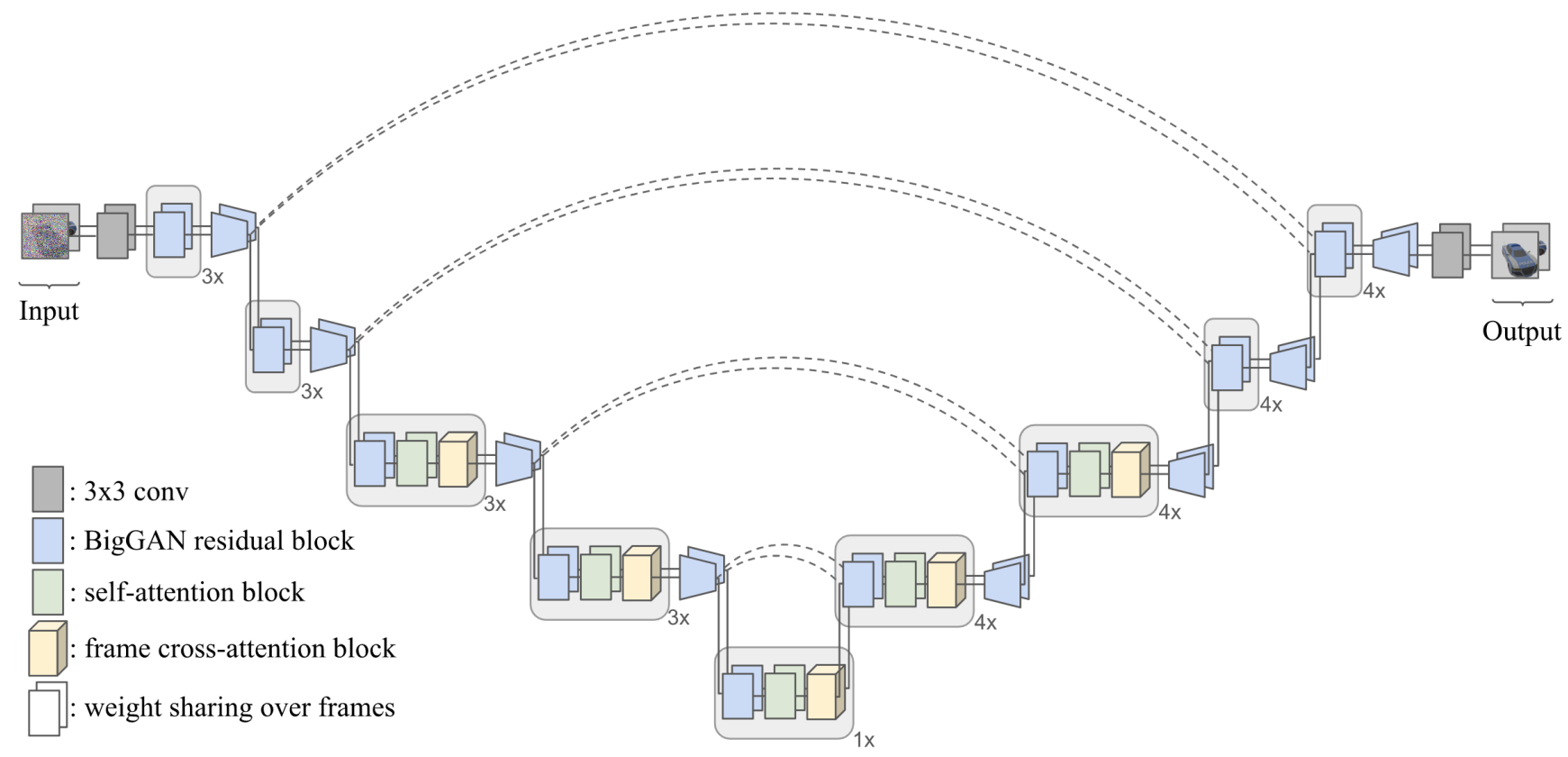
3DiM 모델에는 컨디셔닝 프레임과 noise 프레임을 모두 입력으로 사용하는 신경망 아키텍처가 필요하다. 이를 위한 자연스러운 방법 중 하나는 단순히 채널 차원을 따라 두 이미지를 concat하고 표준 UNet 아키텍처를 사용하는 것이다. 이 “Concat-UNet”은 image-to-image diffusion model의 이전 연구들에서 상당한 성공을 거두었다. 그러나 초기 실험에서 저자들은 Concat-UNet이 매우 열악한 결과를 산출한다는 것을 발견했다. 심각한 3D 불일치가 있었고 컨디셔닝 이미지에 대한 정렬이 부족했다. 저자들은 제한된 모델 용량과 학습 데이터가 주어지면 self-attention에만 의존하는 복잡하고 비선형적인 이미지 변환을 학습하기 어렵다는 가설을 세웠다. 따라서 X-UNet을 도입한다. 핵심 변경 사항은

1. 두 view 각각을 처리하기 위한 파라미터 공유
2. 두 view 사이의 cross-attention 사용

X-UNet 아키텍처는 3D novel view synthesis에 매우 효과적이다.

DDPM을 따라 residual block과 self-attention과 함께 UNet을 사용한다. 또한 Video Diffusion Model에서 영감을 얻어 모든 convolution 및 self-attention 레이어에 대해 두 개의 입력 프레임에 대한 가중치를 공유하지만 몇 가지 중요한 차이점이 있다.

1. 각 프레임이 고유한 noise level을 갖도록 한다. 깨끗한 프레임에 대해 $\lambda_\textrm{max}$의 위치 인코딩을 사용한다. Video Diffusion Model은 반대로 각각 동일한 noise level에서 동시에 여러 프레임을 denoise한다.
2. Video Diffusion Model과 비슷하게 FiLM을 통해 각 UNet 블록을 변조하지만 noise level 임베딩만 사용하는 것과 달리 포즈 인코딩과 noise level 위치 인코딩의 합계를 사용한다. 포즈 인코딩은 프레임과 동일한 차원이라는 점에서 추가로 다르며, Scene representation transformer에서 사용되는 것과 동일한 카메라 광선이다.
3. Video Diffusion Model과 같이 각 self-attention 레이어 뒤에 “시간”에 대하여 attention을 하는 대신, 두 개의 attention 가중치만 수반하며, cross-attention layer을 정의하고 각 프레임의 feature map이 이 layer를 호출하여 다른 프레임의 feature map을 쿼리하도록 한다.

Experiments

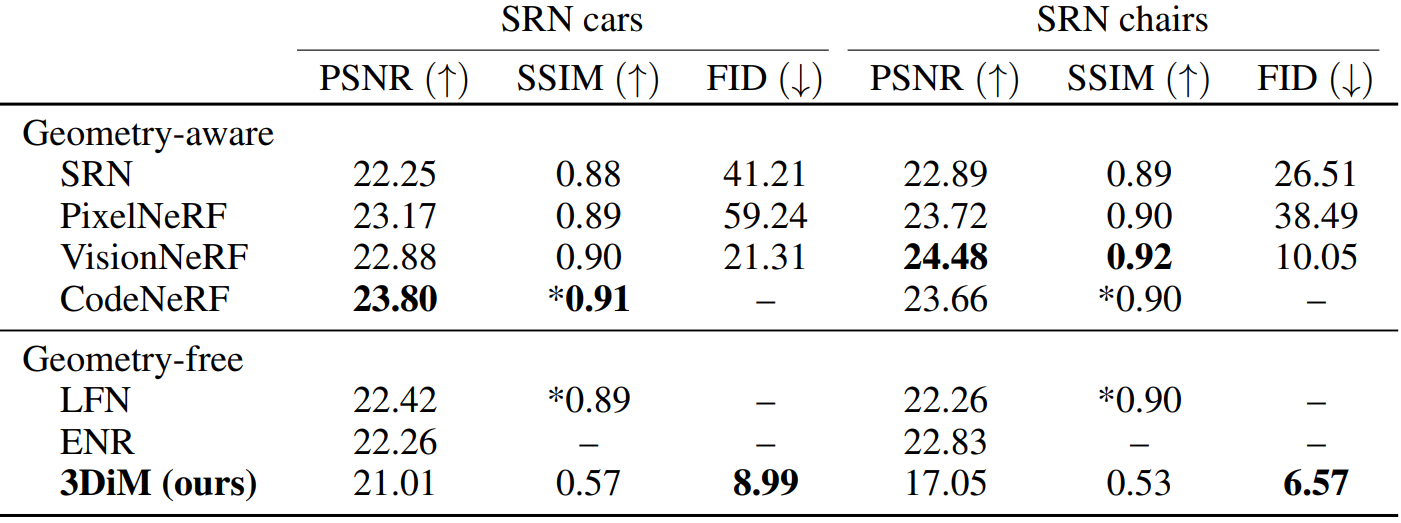
다음은 3DiM의 SRN ShapeNet benchmark에서의 결과를 이전 연구들과 비교한 표이다.

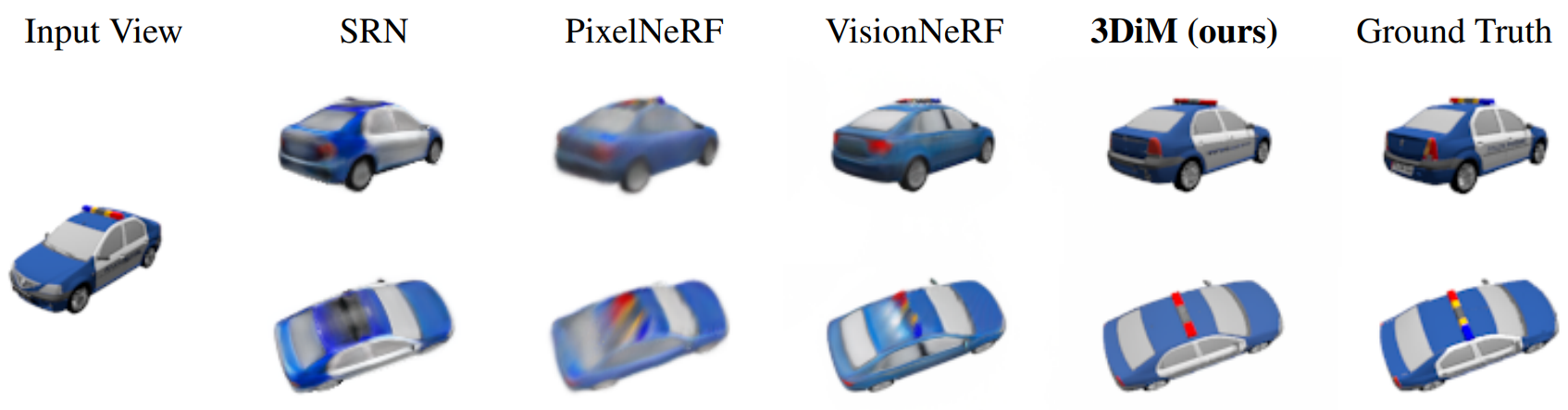
다음은 SRN cars 데이터셋에서 학습한 3DiM의 입력 및 출력 view의 예시이며, 기존 geometry-aware 방법들과 비교한 것이다.

1. Ablation Studies

다음은 3DiM의 ablation study 결과이다. “regression”은 diffusion 전부를 제거하고 regression model을 사용한 것이다.

다음은 ablation의 입력 및 출력 view 예시이다.

2. UNet Architecture Comparisons

다음은 X-UNet과 Concat-UNet을 사용했을 때의 성능을 비교한 표이다.

Evaluating 3D Consistency in Geometry-Free View Synthesis

표준화된 metric들은 geometry-free novel view synthesis model에 적용될 때 실패하는 경우가 있다. 예를 들어 3D 일관성을 성공적으로 측정할 수 없으며 더 나쁜 모델로 개선할 수 있다.

저자들은 colored density field의 볼륨 렌더링이 설계에 따라 3D 일관성이 있다는 사실을 활용하여 “3D 일관성 점수”라는 추가 평가 체계를 제안하였다. Metric은 다음 요구 사항을 충족해야 한다.

1. 3D 일관성이 없는 출력에 페널티를 부여해야 한다.
2. 3D 일관성이 있지만 ground-truth에서 벗어난 출력에 페널티를 주지 않아야 한다.
3. 컨디셔닝 view와 일치하지 않는 출력에 페널티를 부여해야 한다.

두 번째 요구 사항을 충족하기 위해 출력 렌더링을 ground-truth view와 비교할 수 없다. 따라서 모든 요구 사항을 충족하는 한 가지 직접적인 방법은 다음과 같다.

1. 주어진 하나의 view에 대하여 geometry-free model에서 많은 view를 샘플링한다.
2. 이러한 view의 일부에서 NeRF와 같은 neural field를 학습시킨다.
3. 나머지 view에서 neural field 렌더링을 비교하는 일련의 metric을 계산한다.

이렇게 하면 geometry-free model이 일관되지 않은 view를 출력하는 경우 neural field 학습이 방해를 받고 고전적인 이미지 평가 metric이 이를 명확하게 반영해야 한다. 또한 세 번째 요구 사항을 적용하기 위해 학습 데이터의 일부로 나머지를 생성하는 데 사용된 컨디셔닝 view를 포함하기만 하면 된다. 제안된 평가 체계에서 다른 메트릭을 사용할 수 있지만 held-out view에서 PSNR, SSIM, FID를 측정한다.

3D 일관성 점수는 다음과 같다.