[논문리뷰] 3DGUT: Enabling Distorted Cameras and Secondary Rays in Gaussian Splatting
CVPR 2025. [Paper] [Page]
Qi Wu, Janick Martinez Esturo, Ashkan Mirzaei, Nicolas Moenne-Loccoz, Zan Gojcic
NVIDIA | University of Toronto
17 Dec 2024

Introduction
3D Gaussian Splatting (3DGS)의 높은 FPS는 효율적인 rasterization 덕분이다. 그러나 rasterization에 대한 이러한 의존성은 또한 몇 가지 고유한 한계를 부과한다.
- 3DGS에서 사용하는 EWA splatting 공식은 롤링 셔터와 같은 복잡한 시간에 따른 효과를 지원하지 않는다.
- Rasterization은 반사, 굴절, 그림자와 같은 현상을 표현하는 데 필요한 secondary ray를 시뮬레이션할 수 없다.
최근 연구에서는 rasterization 대신 ray tracing을 사용하여 입자를 렌더링하는 것이 제안되었다. 이는 rasterization의 단점을 완화하지만 렌더링 속도가 크게 감소하는 대가를 치른다. 대신, 본 논문에서는 rasterization에 머무르면서 3DGS의 한계를 극복하고 높은 렌더링 속도를 유지하는 것을 목표로 한다.
3DGS는 3D Gaussian을 카메라 이미지 평면에 projection하기 위해 non-linear projection function의 Jacobian을 계산해야 하는 EWA splatting 공식에 의존한다. 이는 완벽한 핀홀 카메라에서도 근사 오차를 발생시키고, 근사 오차는 카메라의 왜곡이 증가함에 따라 점점 더 심해진다. 게다가 EWA splatting 공식 내에서 롤링 셔터와 같은 시간에 따른 효과를 표현하는 방법조차 불분명하다.
Non-linear projection function을 근사화하는 대신, 본 논문에서는 무향 칼만 필터(Unscented Kalman Filter, UKF)에서 영감을 얻어 신중하게 선택된 시그마 포인트들을 사용하여 3D Gaussian을 근사화한다. 이러한 시그마 포인트는 각 포인트에 임의의 projection function을 적용하여 카메라 이미지 평면에 정확하게 projection할 수 있으며, 그 후 2D Gaussian을 무향 변환(Unscented Transform, UT)의 형태로 재추정할 수 있다. 더 나은 근사 품질 외에도, UT는 각 카메라 모델에 대한 Jacobian을 도출할 필요성을 완전히 없애준다. 게다가 롤링 셔터 왜곡과 같은 복잡한 효과는 각 시그마 포인트를 서로 다른 extrinsic matrix로 변환하여 직접 표현할 수 있다.
본 논문은 rasterization 렌더링 공식을 ray tracing 공식과 맞추기 위해 3DGRT를 따르고, StopThePop과 유사한 순서로 정렬하면서 3D 공간에서 입자의 response를 평가한다. 약간의 차이가 있지만 이를 통해 rasterization되고 ray tracing될 수 있는 표현을 제공하여 secondary ray를 사용할 수 있다.
Method
1. Unscented Transform
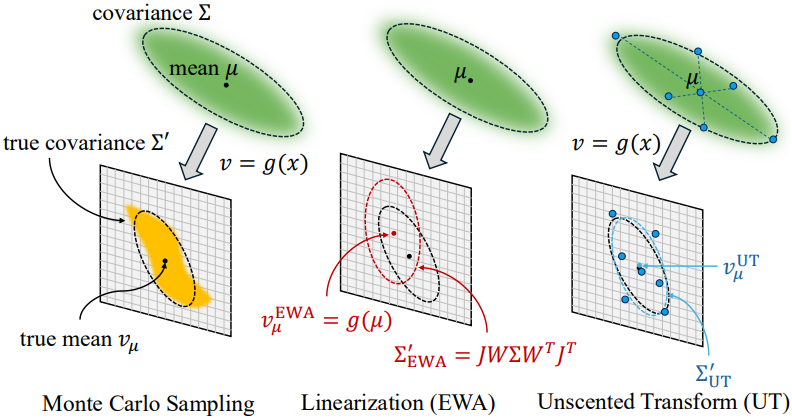
3DGS에서 3D Gaussian을 카메라 이미지 평면에 projection하기 위해 사용되는 EWA splatting 공식은 projective transform의 affine approximation의 선형화에 의존한다. 그러나 이 방식에는 몇 가지 한계점이 있다.
- 테일러 전개에서 고차 항을 무시하여 완벽한 핀홀 카메라에서도 projection error가 발생하고 이러한 오차는 카메라 왜곡과 함께 증가한다.
- 각 특정 카메라 모델에 대해 새로운 Jacobian을 도출해야 하므로 번거롭고 오류가 발생하기 쉽다.
- Projection을 하나의 함수로 표현해야 하는데, 롤링 셔터와 같은 시간에 따른 효과를 고려할 때 특히 어렵다.
이러한 한계를 극복하기 위해, 본 논문은 무향 변환(Unscented Transform, UT)의 아이디어를 기반으로 하고, 대신 신중하게 선택된 시그마 포인트 집합을 사용하여 Gaussian을 근사화하는 것을 제안하였다. 구체적으로, 입자의 위치가 $\boldsymbol{\mu}$이고 공분산 행렬이 $\boldsymbol{\Sigma}$인 경우, 시그마 포인트 \(\mathcal{X} = \{\textbf{x}_i\}_{i=0}^6\)은 다음과 같이 정의된다.
\[\begin{equation} \textbf{x}_i = \begin{cases} \boldsymbol{\mu} & \textrm{for} \; i = 0 \\ \boldsymbol{\mu} + \sqrt{(3 + \lambda)\boldsymbol{\Sigma}_{[i]}} & \textrm{for} \; i = 1, 2, 3 \\ \boldsymbol{\mu} - \sqrt{(3 + \lambda)\boldsymbol{\Sigma}_{[i-3]}} & \textrm{for} \; i = 4, 5, 6 \end{cases} \end{equation}\]각 시그마 포인트에 대한 가중치 \(\mathcal{W} = \{w_i\}_{i=0}^6\)은 다음과 같다.
\[\begin{aligned} w_i^\mu &= \begin{cases} \frac{\lambda}{3 + \lambda} & \textrm{for} \; i = 0 \\ \frac{1}{2(3+\lambda)} & \textrm{for} \; i = 1, \ldots, 6 \end{cases} \\ w_i^\Sigma &= \begin{cases} \frac{\lambda}{3 + \lambda} + (1 - \alpha^2 + \beta) & \textrm{for} \; i = 0 \\ \frac{1}{2(3+\lambda)} & \textrm{for} \; i = 1, \ldots, 6 \end{cases} \end{aligned}\]여기서 $\lambda = \alpha^2 (3 + \kappa) - 3$이며, $α$는 평균 주위로 포인트들의 분포를 제어하는 hyperparameter이고, $\kappa$는 스케일링 파라미터이고, $\beta$는 분포에 대한 prior를 통합하는 데 사용된다.
각 시그마 포인트는 non-linear projection function $g$를 사용하여 카메라 이미지 평면에 독립적으로 projection될 수 있다.
\[\begin{equation} \textbf{v}_{x_i} = g(\textbf{x}_i) \end{equation}\]2D conic은 projection된 시그마 포인트들을 각 가중치로 가중한 선형 결합으로 근사될 수 있다.
\[\begin{aligned} \textbf{v}_{\boldsymbol{\mu}} &= \sum_{i=0}^6 w_i^\mu \textbf{v}_{x_i} \\ \textbf{v}_{\boldsymbol{\Sigma}} &= \sum_{i=0}^6 w_i^\Sigma (\textbf{v}_{x_i} - \textbf{v}_{\boldsymbol{\mu}}) (\textbf{v}_{x_i} - \textbf{v}_{\boldsymbol{\mu}})^\top \end{aligned}\]2D conic을 계산하면, 3DGS와 동일한 tiling과 culling 절차를 적용하여 어떤 입자가 어떤 픽셀에 영향을 미치는지 확인할 수 있다. 다만, 입자의 response 평가는 2D conic에 의존하지 않는다. 대신, UT는 가속 구조로만 작용하여 각 픽셀에 기여하는 입자를 효율적으로 결정하므로 non-linear projection function을 통한 backward pass를 계산할 필요가 없다.
2. Evaluating Particle Response
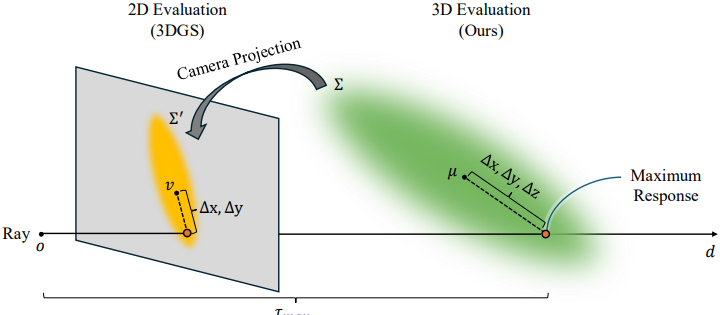
각 픽셀에 기여하는 Gaussian 입자를 식별한 후에는, 해당 입자의 response를 평가하는 방법을 결정해야 한다. 3DGRT를 따라 주어진 광선에서 최대 입자 response 지점에 위치한 하나의 샘플을 사용하여 3D에서 직접 입자를 평가한다.
구체적으로, 광선 $\textbf{r}(\tau)$에 대하여 입자의 response를 최대화하는 거리 \(\tau_\textrm{max}\)를 다음과 같이 계산한다.
\[\begin{equation} \tau_\textrm{max} = \frac{(\boldsymbol{\mu} - \textbf{o})^\top \boldsymbol{\Sigma}^{-1} \textbf{d}}{\textbf{d}^\top \boldsymbol{\Sigma}^{-1} \textbf{d}} = \frac{-\textbf{o}_g^\top \textbf{d}_g}{\textbf{d}_g^\top \textbf{d}_g} \\ \textrm{where} \; \textbf{o}_g = \textbf{S}^{-1} \textbf{R}^\top (\textbf{o} - \boldsymbol{\mu}), \; \textbf{d}_g = \textbf{S}^{-1} \textbf{R}^\top \textbf{d} \end{equation}\]2D에서 입자를 평가하는 3DGS와 달리, 3DGUT는 projection function을 통해 gradient를 전파하지 않으므로 근사를 피하고 잠재적인 수치 불안정성을 완화한다.
3. Sorting Particles
제안된 렌더링 방정식과 입자 평가는 3DGRT에서 사용된 것과 동등하다. 그러나 3DGRT는 전용 가속 구조 덕분에 광선을 따라 정확한 \(\tau_\textrm{max}\) 순서로 충돌 입자를 수집할 수 있는 반면, 3DGS는 각 타일에 대해 글로벌하게 정렬한다.
\(\tau_\textrm{max}\) 순서의 더 나은 근사값을 얻기 위해, StopThePop을 따라 multi-layers alpha blending (MLAB) 근사를 사용한다. 이는 광선별로 $k$개의 가장 먼 충돌 입자를 buffer에 저장하고, buffer에 저장할 수 없는 가까운 충돌들은 점진적으로 알파 블렌딩된다 (투과율이 거의 0이 될 때까지).
4. Implementation and Training
저자들은 컴퓨팅 집약적 부분에 커스텀 CUDA 커널을 사용하였다. 또한 StopThePop이 제안한 culling 전략을 사용하였다. 공정한 비교를 보장하고 모든 평가에서 일관성을 유지하기 위해 3DGS의 모든 파라미터를 채택하였다.
3DGS와 같이 2D screen space gradient를 사용할 수 없으므로, 3DGRT를 따라 3D 위치 gradient를 카메라까지의 거리의 절반으로 나눈 값을 사용하고 300 iteration마다 densification과 pruning을 수행한다. UT의 경우, $\alpha = 1.0$, $\beta = 2.0$, $\kappa = 0.0$으로 설정되었다. L2 loss \(\mathcal{L}_2\)와 perceptual loss \(\mathcal{L}_\textrm{SSIM}\)의 가중 합을 사용하여 3만 iteration 동안 학습시킨다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_2 + 0.2 \mathcal{L}_\textrm{SSIM} \end{equation}\]Experiments
1. Novel View Synthesis Benchmarks
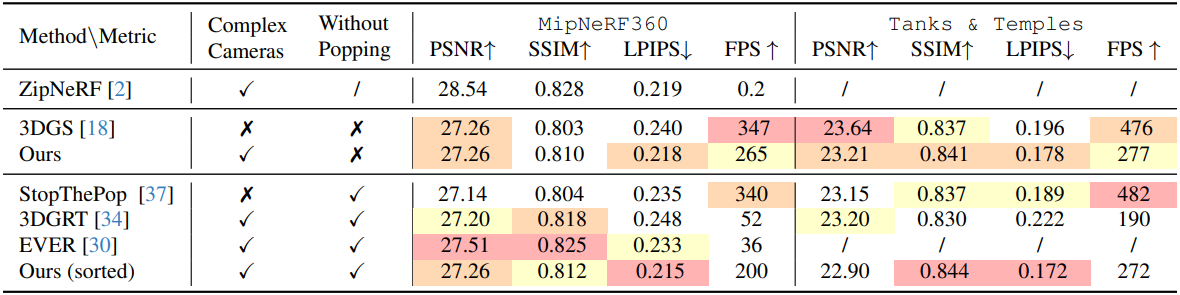
다음은 novel view synthesis (NVS)에 대한 비교 결과이다.

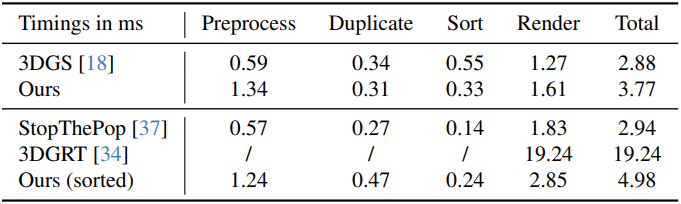
다음은 각 프로세스에 소요되는 시간을 비교한 표이다. (MipNeRF360)
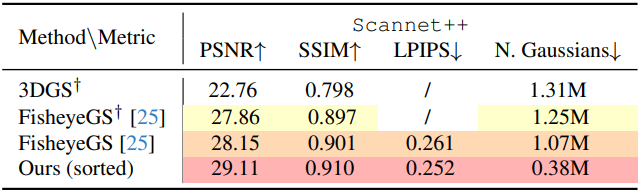
다음은 fisheye camera에 대한 평가 결과이다.

다음은 Waymo 데이터셋에서 NVS 결과를 비교한 표이다.

2. Applications
다음은 롤링 셔터에 대한 비교 결과이다.

다음은 서로 다른 방법으로 학습한 방법들을 3DGRT로 렌더링한 결과이다.

다음은 반사와 굴절에 대한 렌더링 예시이다.
