[논문리뷰] 3D Gaussian Splatting as Markov Chain Monte Carlo

NeurIPS 2024 (Spotlight). [Paper] [Page] [Github]
Shakiba Kheradmand, Daniel Rebain, Gopal Sharma, Weiwei Sun, Jeff Tseng, Hossam Isack, Abhishek Kar, Andrea Tagliasacchi, Kwang Moo Yi
University of British Columbia | Google Research | Google DeepMind | Simon Fraser University | University of Toronto
15 Apr 2024

Introduction

기존 3D Gaussian Splatting (3DGS) 기반 방법들의 공통적인 단점은 Gaussian을 배치하기 위해 대부분 동일한 초기화 및 densification 전략에 의존한다는 것이다. 특히, Gaussian을 배치하기 위해 신중하게 설계된 휴리스틱에 의존한다. 각 Gaussian의 상태에 따라 복제(cloning), 분할(splitting) 또는 제거(pruning)되며 이는 3DGS 표현 내에서 Gaussian 수를 제어하는 ​​주요 방법이다. 게다가 floater를 제거하기 위해 불투명도를 작은 값으로 설정하여 Gaussian을 정기적으로 리셋시킨다. 이 휴리스틱 기반 접근 방식은 신중하게 조정해야 하는 여러 hyperparameter가 필요하며, 일부 장면에서는 실패할 수 있다.

이러한 휴리스틱은 다양한 문제를 야기한다. 특히 실제 장면에 적용할 경우, 이 방법이 제대로 작동하려면 초기 포인트 클라우드에 크게 의존해야 한다. 또한 hyperparameter만으로 주어진 장면에 사용될 3D Gaussian의 개수를 추정하는 것도 쉽지 않아 inference 시간 동안 재구성 품질에 영향을 주지 않고 미리 계산 및 메모리 예산을 제어하기 어렵다. 경우에 따라 Gaussian의 최적 배치가 이루어지지 않아 렌더링 품질이 저하되고 계산량이 낭비된다.

저자들은 이 문제를 해결하기 위해 3D Gaussian들을 랜덤 샘플, 더 구체적으로는 Markov Chain Monte Carlo (MCMC) 샘플로 다시 생각해 보았다. 이 샘플은 어떤 확률 분포에서 추출한 것으로, 이 Gaussian이 장면을 얼마나 충실하게 재구성하는지에 비례하는 확률 분포이다. 이를 고려하면 기존의 3DGS 업데이트 규칙은 Stochastic Gradient Langevin Dynamics (SGLD) 업데이트와 매우 유사하다. SGLD와의 유일한 차이는 샘플 탐색을 촉진하는 noise 항이다. 따라서 3DGS를 SGLD 프레임워크, 즉 MCMC 알고리즘으로 재구성한다. 이는 자연스럽게 장면 풍경을 탐색하고 장면을 충실하게 재현하는 데 효과적인 Gaussian을 샘플링한다. Gaussian 자체가 이미 분포를 표현하고 있으므로 확률 분포를 명시적으로 모델링할 필요가 없다.

이러한 관점에서, Gaussian의 densification 및 pruning, 그리고 불투명도 리셋과 관련된 휴리스틱은 더 이상 필요하지 않다. 3D Gaussian은 단순히 MCMC에 사용되는 샘플일 뿐이므로, 샘플 위치 탐색은 자연스럽게 SGLD 업데이트를 통해 처리된다. Gaussian 집합에 대한 모든 수정은 deterministic한 state transition, 즉 Gaussian 재배치로 재구성될 수 있다. 여기서 샘플(Gaussian 집합)을 다른 샘플(구성이 다른 또 다른 Gaussian 집합)로 이동한다. 중요한 것은 MCMC 샘플링 체인의 교란을 최소화하기 위해 이동 전후의 두 state가 유사한 확률을 갖도록 하는 것이다. 이는 Gaussian의 개수와 같은 조합적 속성을 변경하더라도 학습 loss 값이 변하지 않음을 의미하며, 학습 과정이 불안정해지는 것을 방지한다. MCMC 프레임워크에 따른 이 간단한 전략은 기존의 휴리스틱이 제공하는 것보다 훨씬 높은 품질의 렌더링을 제공한다.

구체적으로, 복제(cloning) 전략을 사용하여 Gaussian을 재배치하는 것을 제안하였다. 즉, 불투명도가 낮은 죽은 Gaussian을 다른 살아있는 Gaussian이 있는 곳으로 옮기는 것이다. 렌더링과 Gaussian의 확률 분포에 미치는 영향을 최소화하기 위해 복제된 Gaussian의 구성을 복제 전과 동일한 이미지를 렌더링하도록 설정한다. 또한, Gaussian의 효율적인 사용을 장려하기 위해 L1 정규화를 적용한다. Gaussian의 범위는 불투명도와 스케일로 정의되므로, 정규화를 두 가지 모두에 적용한다. 이를 통해 불필요한 Gaussian이 사라지도록 효과적으로 유도할 수 있다.

Method

1. 3D Gaussian Splatting as Markov Chain Monte Carlo (MCMC)

기존의 3DGS 접근법과는 달리, 본 연구에서는 Gaussian 분포를 배치하고 최적화하는 학습 과정을 샘플링 과정으로 해석하고자 한다. Loss function을 정의하고 단순히 local minimum으로 나아가는 대신, 학습 이미지를 충실하게 재구성하는 Gaussian 분포 집합에 높은 확률을 부여하는 분포 $\mathcal{G}$를 정의한다. 이러한 선택을 통해 MCMC 프레임워크의 힘을 활용하여 파라미터 공간에서 discrete한 변화를 주더라도 수학적으로 잘 동작하는 방식으로 이 분포에서 샘플을 추출할 수 있다. 따라서 일반적인 기울기 기반 최적화의 기본이 되는 연속성 가정을 깨지 않고 3DGS의 여러 휴리스틱과 유사한 discrete한 연산을 설계할 수 있다.

이를 달성하기 위해, 최근 novel view synthesis에 적용된 MCMC 프레임워크인 Stochastic Gradient Langevin Dynamics (SGLD) 방법부터 시작한다. 구체적으로, 3DGS에서 단일 Gaussian 행렬 $\textbf{g}$의 업데이트를 고려하고, 분할/병합 휴리스틱을 무시한다면 다음과 같다.

\[\begin{equation} \textbf{g} \leftarrow \textbf{g} - \lambda_\textrm{lr} \cdot \nabla_\textbf{g} \mathbb{E}_{\textbf{I} \sim \mathcal{I}} [\mathcal{L}_\textrm{total} (\textbf{g}; \textbf{I})] \end{equation}\]

(\(\lambda_\textrm{lr}\)은 learning rate, $\textbf{I}$는 학습 이미지 집합 $\mathcal{I}$에서 샘플링된 이미지)

위 식을 일반적인 SGLD 업데이트와 비교해 보자.

\[\begin{equation} \textbf{g} \leftarrow \textbf{g} + \alpha \cdot \nabla_\textbf{g} \log \mathcal{P} (\textbf{g}) + b \cdot \boldsymbol{\epsilon} \end{equation}\]

여기서 $\mathcal{P}$는 샘플링하려는 분포에 대한 확률 밀도 함수이고, $\boldsymbol{\epsilon}$는 탐색을 위한 noise 분포이다. Hyperparameter $a$와 $b$는 수렴 속도와 탐색 간의 상충 관계를 제어한다. 위의 두 식 사이에는 놀라운 유사성이 있다. 다시 말해, loss를 분포의 negative log likelihood로 두면,

\[\begin{equation} \mathcal{G} = \mathcal{P} \propto \exp (- \mathcal{L}_\textrm{total}) \end{equation}\]

\(\lambda_\textrm{lr} = -a\)이고 $b = 0$이면 방정식이 동일해진다. 따라서 3DGS 최적화는 렌더링 품질과 관련된 likelihood 분포에서 샘플링된 Gaussian을 갖는 것으로 볼 수 있다. 또한 최적화에 noise를 추가하는 것은 noise를 주입하거나 perturbed gradient descent를 수행하는 기존 최적화 방법과 밀접한 관련이 있음을 알 수 있다.

2. Updating with Stochastic Gradient Langevin Dynamics

SGLD와 기존 3DGS 최적화 간의 연결을 고려하여, Gaussian $\textbf{g}$의 업데이트를 다음과 같이 다시 쓸 수 있다.

\[\begin{equation} \textbf{g} \leftarrow \textbf{g} - \lambda_\textrm{lr} \cdot \nabla_\textbf{g} \mathbb{E}_{\textbf{I} \sim \mathcal{I}} [\mathcal{L}_\textrm{total} (\textbf{g}; \textbf{I})] + \lambda_\textrm{noise} \cdot \boldsymbol{\epsilon} \end{equation}\]

실제로는 \(\nabla_\textbf{g} \mathbb{E}_{\textbf{I} \sim \mathcal{I}} [\mathcal{L}_\textrm{total} (\textbf{g}; \textbf{I})]\) 대신 기본 파라미터 \(\beta_1\)과 \(\beta_2\)를 갖는 Adam optimizer를 사용한다.

위 식에서 noise 항 $\boldsymbol{\epsilon}$을 신중하게 설계하는 것이 중요하다. $\boldsymbol{\epsilon}$은 기울기 항 \(\nabla_{\textbf{g}_i} \mathcal{L}_\textrm{total}\)에 의해 균형을 이룰 수 있도록 추가해야 하며, 그렇지 않으면 위 식은 랜덤 업데이트에 가까워진다. 추가된 noise로 인해 Gaussian이 이전 영역 외부로 이동하게 되면, 이러한 무작위 이동은 복구 불가능해져 MCMC 샘플링 체인이 손상될 수 있다.

또한, 불투명도, 크기, 색상에는 noise를 추가하지 않으며, 실제로 이러한 파라미터에 noise를 추가하면 성능이 약간 저하된다. 반대로, 초기화 시에 누락된 점 등으로 인해 공간 영역이 탐색되지 않은 상태로 남아 있을 경우 3DGS 재구성에 상당한 악영향을 미칠 수 있다. 이는 noise 기반 탐색을 통해 랜덤 초기화뿐만 아니라 SFM 기반 초기화의 결과도 개선할 수 있음을 시사한다.

마지막으로, 탐색뿐만 아니라 수렴 품질에도 관심이 있으므로, Gaussian이 잘 동작할 때, 즉 Gaussian의 불투명도가 기울기에 의해 잘 유도될 만큼 충분히 높을 때 noise 양을 줄인다. 따라서 Gaussian의 위치에 대해서만 noise 항을 설계하여, Gaussian의 공분산과 불투명도, learning rate에 따라 달라지도록 한다.

\[\begin{equation} \boldsymbol{\epsilon}_\mu = \lambda_\textrm{lr} \cdot \sigma (-k(t-o)) \cdot \boldsymbol{\Sigma}_\eta \quad \textrm{where} \quad \boldsymbol{\epsilon} = [\boldsymbol{\epsilon}_\mu, \textbf{0}] \end{equation}\]

($\eta \sim \mathcal{N}(\textbf{0},\textbf{I})$, $\sigma$는 sigmoid 함수, $k$와 $t$는 sigmoid의 선명도를 제어하는 ​hyperparameter)

Gaussian의 불투명도 값에 대한 3DGS의 pruning threshold를 중심으로 0에서 1까지 변화하는 날카로운 transition function을 만들기 위해 $k=100$, $t=0.005$로 설정한다. 위 식은 Gaussian의 $\boldsymbol{\Sigma}$와 동일한 이방성의 noise로 Gaussian을 섭동시키며, sigmoid 항은 불투명한 Gaussian에 대한 noise의 영향을 줄인다.

3. Heuristics as state transitions via relocation

3DGS의 휴리스틱을 간단한 state transition으로 다시 쓸 수 있는 방법이 필요하다. 3DGS에서 휴리스틱은 Gaussian을 이동, 분할, 복제, 제거, 추가하여 더 많은 살아있는 Gaussian ($o_i \ge 0.005$)을 장려하는 데 사용된다. 이러한 모든 수정 사항을 한 샘플 state $\textbf{g}^\textrm{old}$에서 다른 샘플 state $\textbf{g}^\textrm{new}$로 이동하는 것으로 설명한다. 이는 Gaussian 수가 변경되는 경우에도 적용된다. Gaussian 수가 적은 상태를 더 많은 Gaussian을 가진 동등한 상태로 생각할 수 있지만 불투명도가 0인 상태, 즉 죽은 Gaussian으로 생각할 수 있기 때문이다.

중요한 점은 이러한 종류의 결정론적 동작을 MCMC 프레임워크에 통합하기 위해 MCMC 샘플링이 붕괴되지 않도록 하는 것이 중요하다. 구체적으로, 이동 전후의 state 확률, 즉 $\mathcal{P}(\textbf{g}^\textrm{new}) = \mathcal{P}(\textbf{g}^\textrm{old})$를 보존하는 것을 목표로 한다. 이렇게 하면 이동은 단순히 동일한 확률로 다른 표본으로 이동하는 것으로 간주될 수 있다.

다양한 방법이 있지만, 여기서는 불투명도가 0.005보다 작은 죽은 Gaussian을 살아있는 Gaussian의 위치로 옮기는 간단한 전략을 선택하였다. 이 과정에서 $\textbf{g}^\textrm{new}$와 $\textbf{g}^\textrm{old}$가 렌더링에 미치는 영향의 차이를 최소화하도록 Gaussian의 파라미터를 설정한다. 일반성을 잃지 않고 $N-1$개의 Gaussian \(\textbf{g}_{1, \ldots, N-1}\)을 \(\textbf{g}_N\)으로 옮기는 것을 고려해 보자. 그러면 다음과 같이 업데이트 하면 된다.

\[\begin{aligned} \boldsymbol{\mu}_{1, \ldots, N}^\textrm{new} &= \boldsymbol{\mu}_N^\textrm{old}, \qquad o_{1, \ldots, N}^\textrm{new} = 1 - (1 - o_N^\textrm{old})^{1/N} \\ \boldsymbol{\Sigma}_{1, \ldots, N}^\textrm{new} &= (o_N^\textrm{old})^2 \left( \sum_{i=1}^N \sum_{k=0}^{i-1} \left( \binom{i-1}{k} \frac{(-1)^k (o_N^\textrm{new})^{k+1}}{\sqrt{k+1}} \right) \right)^{-2} \boldsymbol{\Sigma}_N^\textrm{old} \end{aligned}\]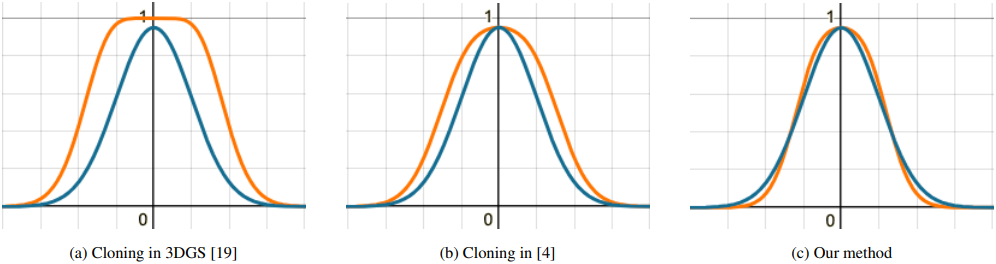 (파란색: 복제 전 / 주황색: 복제 후)

이 전략이 3DGS의 cloning과 비슷해 보일 수 있지만, 위 그림에서 볼 수 있듯이, 기존 cloning과 최근 제안된 중앙 보정 버전은 모두 복제될 때 rasterize된 Gaussian에 상당한 차이를 초래한다. 두 가지 기존 전략 모두 선택된 Gaussian의 범위가 커지므로 state의 유사성 측면에서 $\mathcal{P}(\textbf{g}^\textrm{new}) \ne \mathcal{P}(\textbf{g}^\textrm{old})$이다.

본 논문의 방법은 $\mathcal{P}(\textbf{g}^\textrm{new}) \approx \mathcal{P}(\textbf{g}^\textrm{old})$라는 결과를 가져오지만, 정확하지는 않다. 따라서 학습 과정의 중단을 방지하기 위해 100 iteration마다 이 이동을 적용한다. 이동할 위치를 선택하기 위해, 각 죽은 Gaussian에 대해, 불투명도 값에 비례하는 확률로 살아있는 Gaussian의 multinomial sampling을 통해 이동할 타겟 Gaussian을 먼저 선택한다. 모든 이동 결정이 내려진 후에 위 식을 적용한다.

Adam optimizer에 의존하므로 모멘트 통계도 조정해야 한다. 타겟 Gaussian의 모멘트 통계는 리셋시켜 현재 state를 유지하도록 하는 반면, 새로운 Gaussian의 경우 탐색을 장려하기 위해 모멘트 통계를 유지한다. 이는 죽은 Gaussian이 noise 항에 의해 지배되며, 따라서 모멘트 통계가 탐색을 촉진하는 데 적합하기 때문이다.

4. Encouraging fewer Gaussians

메모리와 연산을 효과적으로 활용하면서 성능을 향상시키기 위해, Gaussian이 쓸모없는 위치에서 사라지고 다른 곳에서 재등장하도록 유도한다. Gaussian의 존재 여부는 불투명도 $o$와 공분산 $\boldsymbol{\Sigma}$에 의해 결정되므로, 두 가지 모두에 정규화를 적용한다. 전체 학습 loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{total} = (1 - \lambda_\textrm{D-SSIM}) \cdot \mathcal{L}_1 + \lambda_\textrm{D-SSIM} \cdot \mathcal{L}_\textrm{D-SSIM} + \lambda_o \cdot \sum_i \vert o_i \vert_1 + \lambda_\boldsymbol{\Sigma} \cdot \sum_{ij} \left\vert \sqrt{\textrm{eig}_j (\boldsymbol{\Sigma}_i)} \right\vert_1 \end{equation}\]

(\(\textrm{eig}_j (\cdot)\)는 공분산 행렬의 $j$번째 고유값 (공분산 행렬의 주축들을 대한 분산))

Experiments

1. Results

다음은 동일한 개수의 Gaussian에 대한 비교 결과이다.

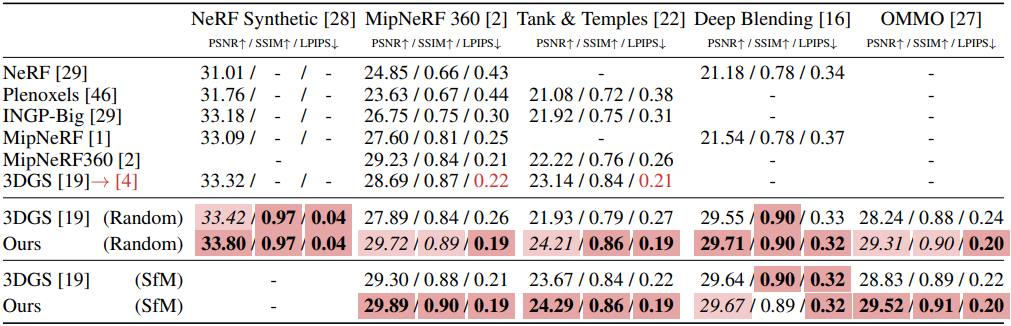
다음은 Gaussian 수에 따른 PSNR을 비교한 결과이다.

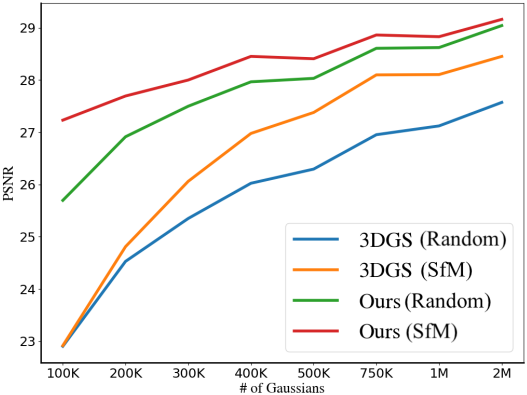
다음은 랜덤 초기화에 대한 결과를 비교한 것이다.

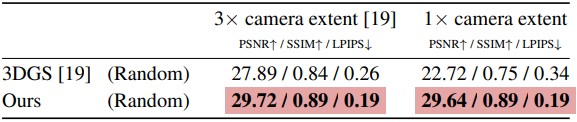
2. Ablations

다음은 ablation study 결과이다.

다음은 noise 항에 대한 ablation 결과이다. (왼쪽이 noise 항을 사용한 경우)

3. Computational time

다음은 학습 시간에 대한 비교 결과이다.