[논문리뷰] 3DGS-Enhancer: Enhancing Unbounded 3D Gaussian Splatting with View-consistent 2D Diffusion Priors
NeurIPS 2024. [Paper] [Page]
Xi Liu, Chaoyi Zhou, Siyu Huang
Clemson University
21 Oct 2024

Introduction
최근 3D Gaussian Splatting (3DGS)은 매우 효율적인 렌더링 파이프라인으로 사실적인 렌더링을 생성하는 데 뛰어난 성능을 보였다. 그러나 기존 시점들에서 멀리 떨어진 고품질의 새로운 뷰를 렌더링하는 것은 여전히 매우 어려운데, 이는 샘플링이 부족한 영역에 정보가 부족하기 때문이다. 위 그림에서 볼 수 있듯이 입력 뷰가 세 개뿐인 경우 눈에 띄는 타원체와 속이 빈 아티팩트가 나타난다. 실제로 이러한 일반적인 저품질 렌더링 결과로 인해 3DGS를 개선하는 것이 필수적이다.
Novel view synthesis (NVS)의 렌더링 품질을 개선하는 것을 목표로 하는 향상 방법에 특별히 초점을 맞춘 이전 연구는 거의 없다. NVS에 대한 대부분의 기존 향상 방법들은 깊이나 normal과 같은 추가적인 기하학적 제약 조건을 3D 재구성 프로세스에 통합하여 관찰된 영역과 관찰되지 않은 영역 간의 격차를 메우는 데 중점을 두었다. 그러나 이러한 방법은 추가 제약 조건의 효과에 크게 의존하며 종종 노이즈에 민감하다. 또 다른 방법은 generative prior를 활용하여 NVS 파이프라인을 정규화하는 것이다. 그러나 생성된 뷰가 입력 뷰와 멀리 떨어져 있는 경우 뷰 일관성이 여전히 떨어진다.
본 논문에서는 3DGS 표현 향상을 위해 2D generative prior, 예를 들어 latent diffusion model (LDM)을 활용하였다. LDM은 다양한 이미지 생성 및 복원 작업에서 강력하고 robust한 생성 능력을 보여주었다. 그럼에도 불구하고 주요 과제는 생성된 2D 이미지 간의 3D 뷰 일관성이 좋지 않다는 것이다. 이는 매우 정밀한 뷰 일관성이 필요한 3DGS 학습 프로세스를 크게 방해한다.
멀티뷰 이미지 간의 시각적 일관성과 동영상 프레임 간의 시간적 일관성에서 영감을 얻어, 저자들은 까다로운 3D 일관성 문제를 동영상 생성 내에서 시간적 일관성을 달성하는 더 쉬운 task로 재구성하여, 고품질 및 뷰 일관성 있는 이미지를 복원하기 위한 강력한 video diffusion model을 활용할 수 있도록 제안하였다. 저자들은 3DGS-Enhancer라는 새로운 3DGS 향상 파이프라인을 제안하였다. 3DGS-Enhancer의 핵심은 video LDM이며, 다음과 같은 구성 요소들로 구성된다.
- 렌더링된 뷰의 latent feature를 인코딩하는 이미지 인코더
- 시간적으로 일관된 latent feature를 복원하는 동영상 기반 diffusion model
- 원래 렌더링된 이미지의 고품질 정보를 복원된 latent feature와 효과적으로 통합하는 spatial-temporal decoder (STD)
3DGS 모델은 이러한 향상된 뷰에 의해 fine-tuning되어 렌더링 성능이 향상된다. 3DGS-Enhancer는 궤적이 없어 sparse한 뷰에서 바인딩되지 않은 장면을 재구성하고 두 개의 알려진 뷰 사이의 보이지 않는 영역에 대한 자연스러운 3D 표현을 생성할 수 있다. 단일 이미지에서 object-level의 3DGS 모델을 생성하기 위해 video LDM을 활용했던 것과 달리, 3DGS-Enhancer는 기존 3DGS 모델을 향상시키는 데 중점을 두므로 더 일반화된 장면에 적용할 수 있다.
Method
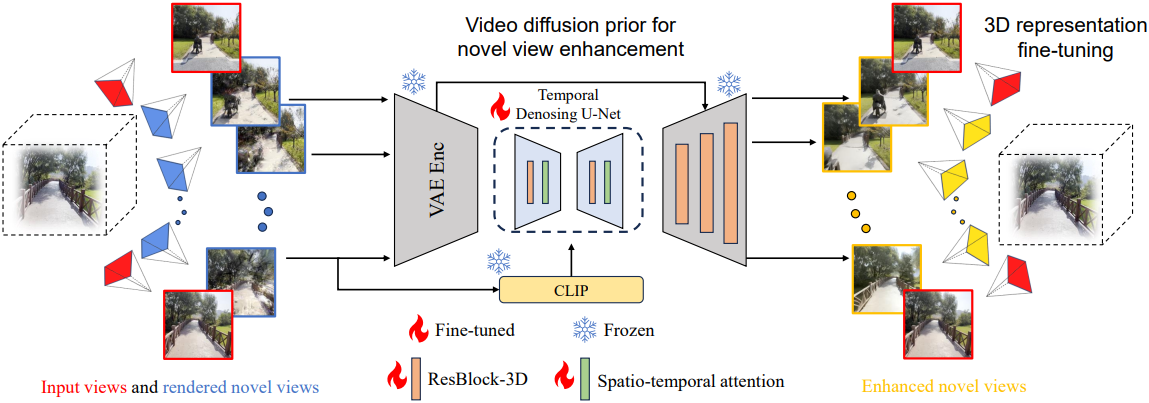
- 입력: 카메라 포즈가 \(\{p_1^\textrm{ref}, \ldots, p_{N_\textrm{ref}}^\textrm{ref}\}\)인 레퍼런스 이미지 \(\{I_1^\textrm{ref}, \ldots, I_{N_\textrm{ref}}^\textrm{ref}\}\)
- 목표: 새로운 뷰에서 3DGS 모델로 렌더링된 이미지 \(\{I_1, \ldots, I_{N_\textrm{new}}\}\)를 향상시키는 것
1. Video Diffusion Prior for Temporal Interpolation
생성된 2D 동영상 프레임과 고품질 레퍼런스 뷰 간의 일관성을 높이기 위해 동영상 복원 task를 동영상 interpolation task로 공식화한다. 여기서 video diffusion model에 대한 입력의 첫 번째 프레임과 마지막 프레임은 두 개의 레퍼런스 뷰이다.
두 레퍼런스 뷰 사이의 궤적에서 샘플링된 카메라 포즈를 \(\{p_{i-1}^\textrm{ref}, p_1^s, \ldots, p_T^s, p_i^\textrm{ref}\}\)라고 하면 그에 따라 렌더링된 이미지는 \(v = \{I_{i-1}^\textrm{ref}, I_1, I_2, \ldots, I_T, I_i^\textrm{ref}\}\)이다. $v \in \mathbb{R}^{(T+2) \times 3 \times H \times W}$는 Stable Video Diffusion (SVD) 모델과 같은 video diffusion model의 입력으로 사용된다.
CLIP에서 추출한 단일 입력 이미지 feature를 조건부 입력으로 $T$번 사용하는 SVD와 달리, $v$를 CLIP 인코더에 입력하여 일련의 조건부 입력 $c_\textrm{clip}$을 얻고 cross-attention을 통해 video diffusion model에 추가한다. 또한, $v$를 VAE 인코더에 입력하여 latent feature $c_\textrm{vae}$를 얻고 classifier-free guidance를 통해 diffusion model에 추가하여 더 풍부한 색상 정보를 통합한다.
Diffusion U-Net $\epsilon_\theta$는 각 diffusion step $t$에 대한 noise $\epsilon$을 예측하고, loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{diffusion} = \mathbb{E} [\| \epsilon - \epsilon_\theta (z_t, t, c_\textrm{clip}, c_\textrm{vae}) \|] \\ \textrm{where} \quad z_t = \alpha_t z + \sigma_t \epsilon, \; \epsilon \sim \mathcal{N}(0, I) \end{equation}\]학습된 video diffusion model은 렌더링된 저품질 뷰 $v$에 해당하는 향상된 이미지 latent들의 시퀀스 $z_v$를 생성한다.
2. Spatial-Temporal Decoder
이 video diffusion model은 향상된 이미지의 latent $z_v$를 생성할 수 있지만, 원본 video LDM의 디코더 출력에서 시간적 불일치, 블러링, 색상 변형과 같은 아티팩트가 발생한다. 이러한 문제를 해결하기 위해, 저자들은 수정된 spatial-temporal decoder (STD)를 제안하였다. STD는 원본 VAE 디코더와 비교하여 다음과 같은 개선 사항이 있다.
시간적 디코딩 방식
STD는 시간적 일관성을 보장하기 위해 추가적인 temporal convolution layer들을 사용한다. Video diffusion model과 유사하게, 첫 번째와 마지막 입력 프레임은 레퍼런스 뷰 이미지로 사용되고, 중간 입력들은 생성된 뷰들이다.
렌더링된 뷰의 효과적인 통합
STD는 video diffusion model과 동일한 조건부 입력을 사용하여 디코더가 원본 렌더링된 이미지를 더 잘 활용할 수 있도록 한다. 이러한 조건부 입력은 StableSR의 Controllable Feature Warping (CFW) 모듈을 통해 STD에 입력되며, 이를 통해 고주파 패턴이 더 잘 보존된다.
색상 보정
색상 변화 문제를 해결하기 위해 StableSR을 따라 디코딩된 이미지에 색상 정규화를 적용한다. 그러나 조건부 입력의 매우 흐릿하고 품질이 낮은 이미지가 색상 보정 효과를 떨어뜨릴 수 있다. 이를 완화하기 위해 첫 번째 레퍼런스 뷰를 사용하여 평균과 분산을 계산한 다음, 다른 모든 디코딩된 이미지를 이 레퍼런스 뷰에 맞춘다. $I_i^g$를 평균이 $\mu_{I_i^g}$이고 분산이 $\sigma_{I_i^g}$인 $i$번째 디코딩된 이미지라고 하고, \(\hat{I}_0^g\)를 평균이 \(\mu_{\hat{I}_0^g}\)이고 분산이 \(\sigma_{\hat{I}_0^g}\)인 레퍼런스 뷰라고 하면 보정된 이미지 $I_i^c$는 다음과 같이 계산된다.
\[\begin{equation} I_i^c = \frac{I_i^g - \mu_{I_i^g}}{\sigma_{I_i^g}} \cdot \sigma_{\hat{I}_0^g} + \mu_{\hat{I}_0^g} \end{equation}\]STD의 loss function은 $I^g$와 GT \(\hat{I}^g\) 사이의 L1 reconstruction loss, LPIPS loss, adversarial loss로 구성된다.
\[\begin{equation} \mathcal{L}_\textrm{STD} = \mathcal{L}_\textrm{rec} (I^g, \hat{I}^g) + \mathcal{L}_\textrm{LPIPS} (I^g, \hat{I}^g) + \mathcal{L}_\textrm{adv} (I^g) \end{equation}\]3. Fine-tuning Strategies of 3D Gaussian Splatting
Confidence-aware 3D Gaussian splatting
렌더링된 뷰의 품질이 상당히 향상되었음에도 불구하고, 3DGS 모델은 복원된 뷰의 약간의 부정확성에 매우 민감하기 때문에 3DGS 모델을 fine-tuning할 때 복원된 새로운 뷰보다는 레퍼런스 뷰에 더 의존해야 한다. 이러한 부정확성은 fine-tuning 프로세스 중에 증폭될 수 있다.
생성된 이미지가 Gaussian 학습에 미치는 부정적인 영향을 최소화하기 위해, 저자들은 confidence-aware 3D Gaussian splatting을 제안하였다. 이 전략은 이미지 레벨과 픽셀 레벨의 두 가지 레벨의 신뢰도를 포함한다. 이미지 레벨의 경우, 실제 이미지에 더 가까운 생성된 이미지는 낮은 신뢰도를 갖는다. 픽셀 레벨의 경우, 이 픽셀을 렌더링하는 데 사용된 모든 Gaussian의 평균 공분산이 클수록 신뢰도가 높아진다.
Image level confidence
NVS에서 두 이미지 뷰에 노이즈가 있는 경우 두 뷰 사이의 거리가 가까우면 충돌이 발생하고 장면의 3D 일관성이 깨질 가능성이 커진다. 따라서 레퍼런스 뷰에 가까운 새로운 뷰의 경우 노이즈의 부정적인 영향을 완화하기 위해 3D Gaussian을 신중하게 최적화하는 것이 중요하다. 반대로 새로운 뷰가 알려진 모든 뷰에서 멀리 떨어져 있는 경우 이미 잘 재구성된 영역을 방해할 가능성이 적다.
이러한 추론에 따라 새로운 뷰에서 레퍼런스 뷰까지의 거리를 0과 1 사이로 정규화한다. 시점이 레퍼런스 뷰에서 멀수록 신뢰도가 높아진다.
Pixel level confidence

위 그림에서 볼 수 있듯이, 잘 재구성된 영역은 일반적으로 매우 작은 볼륨을 가진 Gaussian으로 표현된다. 저자들은 이 관찰을 바탕으로 픽셀 수준 신뢰도를 계산하는 방법을 제안하였다.
3D Gaussian의 스케일링 벡터 $s$가 RGB 색상과 동일한 3차원이기 때문에 유사한 프로세스를 사용하여 $H \times W \times 3$ 이미지를 렌더링할 수 있다. 3DGS-Enhancer에서 scale map의 이 세 채널을 곱하여 픽셀 레벨의 신뢰도를 얻는다. 생성된 이미지의 각 픽셀에 대해 신뢰도가 높을수록 3DGS 모델을 학습시키는 데 더 큰 가중치가 부여된다.
3D Gaussian 집합이 주어지면 3채널 신뢰도 맵 $C_\textrm{conf}$은 색상 렌더링과 동일하게 렌더링된다.
\[\begin{equation} C_\textrm{conf} = \sum_{i \in M} s_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_i) \end{equation}\]1채널 픽셀 레벨 신뢰도 맵 $P_c$는 다음과 같이 정의된다.
\[\begin{equation} P_c = \sqrt[3]{C_\textrm{conf}[0] \times C_\textrm{conf}[1] \times C_\textrm{conf}[2]} \end{equation}\]전반적으로 3D Gaussian에 대한 loss function은 다음과 같이 정의된다.
\[\begin{equation} \mathcal{L}_\textrm{3DGS} = I_c \cdot (P_c \odot \vert C - \hat{C} \vert_1 + \textrm{SSIM} (C, \hat{C})) \end{equation}\]($I_c$는 이미지 레벨 신뢰도 맵, $C$는 렌더링된 이미지, $\hat{C}$는 GT 이미지)
Experiments
- 3DGS-Enhance Dataset
- DL3DV 데이터셋에서 랜덤하게 130개의 장면을 선택하고 15만 개 이상의 이미지 쌍을 구성
- 추가로 20개의 장면을 랜덤하게 선택하여 test set을 구성
1. Comparison with State-of-the-Arts
다음은 DL3DV test set에서의 결과이다.

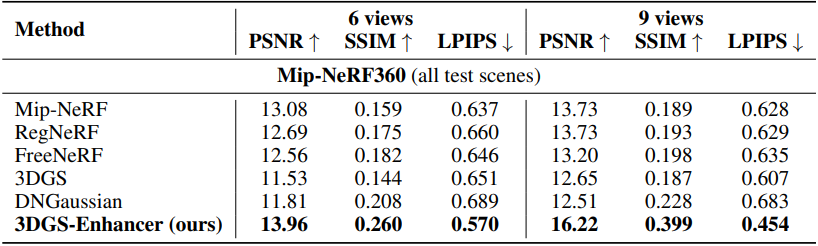
다음은 Mip-NeRF360 데이터셋에서의 결과이다.

2. Ablation Study
다음은 3DGS-Enhancer의 4가지 모듈들에 대한 ablation 결과이다. (입력 뷰가 3, 6, 9, 12개인 경우의 평균)

다음은 video diffusion model 구성 요소에 대한 ablation 결과이다.

다음은 STD와 색상 보정 모듈에 대한 ablation 결과이다. (DL3DV test set, 9-view setting)

Limitation
연속적인 interpolation을 위해 인접한 뷰에 의존하므로 단일 뷰 3D 모델 생성에 쉽게 적용할 수 없다.