[논문리뷰] 3D Gaussian Ray Tracing: Fast Tracing of Particle Scenes
SIGGRAPH Asia 2024. [Paper] [Page]
Nicolas Moenne-Loccoz, Ashkan Mirzaei, Or Perel, Riccardo de Lutio, Janick Martinez Esturo, Gavriel State, Sanja Fidler, Nicholas Sharp, Zan Gojcic
NVIDIA
9 Jul 2024

Introduction
본 논문은 3DGS가 rasterization의 장단점으로 인해 제한된다는 관찰에서 동기를 부여받았다. Tile-based rasterizer는 롤링 셔터 효과로 인해 왜곡이 심한 카메라에서 렌더링하는 데 적합하지 않다. 또한 반사, 굴절, 그림자와 같은 현상을 처리하는 데 필요한 2차 광선(secondary ray)을 효율적으로 시뮬레이션할 수 없다. 또한 rasterization은 stochastic sampling을 할 수 없다. 대신 본 논문은 GPU ray tracing을 위한 맞춤형 구현을 통해 ray tracing된 Gaussian 입자들을 효율적으로 만들어 이러한 제한 사항을 해결하는 것을 목표로 하였다. 본 논문의 목표는 글로벌 조명 또는 역광과 같은 해결되지 않은 문제에 대한 end-to-end 해결 방법을 제공하는 것이 아니라 이러한 문제에 대한 향후 연구에 핵심 알고리즘인 빠르고 미분 가능한 ray tracer를 제공하는 것이다.
Gaussian 장면을 효율적으로 ray tracing하는 것은 해결된 문제가 아니다. 반투명 입자의 ray tracing을 위해 특별히 설계된 기존 알고리즘조차도 엄청난 수의 불균일하게 분포되고 dense하게 겹치는 입자로 인해 이러한 장면 재구성에 효과적이지 않다. 따라서 저자들은 다음과 같은 구성 요소를 사용하여 Gaussian 입자에 대한 맞춤형 GPU 가속 ray tracer를 설계하였다.
- 정렬된 교점을 수집하기 위한 $k$-buffer hits-based marching
- 빠르게 계산할 수 있는 광선-삼각형 교점을 활용하기 위한 bounding mesh proxy
- 최적화를 가능하게 하는 backward pass
이러한 각 구성 요소는 다양한 벤치마크에서 속도와 품질에 대해 신중하게 테스트되었다. 저자들은 알고리즘의 세부 사항을 목표에 맞게 조정하였으며 단순한 첫 번째 구현보다 거의 25배 빠르다.
입자로 장면을 표현하는 기본적인 접근 방식은 Gaussian 커널에만 국한되지 않는다. 최근 연구에서는 이미 몇 가지 자연스러운 일반화를 보여주었다. 본 논문의 ray tracing 체계는 입자 기반 장면 표현에 더 광범위하게 일반화된다.
3DGRT는 멀티뷰 벤치마크에서 3DGS rasterizer 품질과 거의 일치하거나 그 이상이며, 여전히 실시간 렌더링을 달성한다. 더 중요한 것은 그림자 및 반사와 같은 보조 효과, 높은 왜곡 및 롤링 셔터가 있는 카메라의 렌더링, 확률적으로 샘플링된 광선을 사용한 학습 등을 ray tracing을 통해 쉽고 효율적으로 다양한 새로운 기술을 시연할 수 있다는 점이다.
Method
제안된 ray tracer에는 두 가지 핵심 요소가 필요하다.
- 적응형 bounding mesh primitive를 사용하여 입자에 대한 교점을 효율적으로 테스트하기 위해 BVH에 입자를 표현하는 전략
- Ray casting을 하고 교점들의 batch를 수집하는 렌더링 알고리즘
1. Bounding Primitives
모든 ray tracer는 어떻게든 기본 입자를 BVH에 삽입하고 광선이 교차하는 기본 입자를 쿼리해야 한다. 첫 번째 과제는 BVH에 입자를 삽입하는 방법을 결정하고 입자에 대한 교점을 테스트하는 것이다.
NVIDIA OptiX 프로그래밍 모델은 BVH에 삽입할 수 있는 세 가지 기본 유형, 즉 삼각형, 구, axis-aligned bounding box (AABB)를 지원한다. 이러한 옵션은 AABB나 구와 같은 단순한 축 정렬 경계를 구성하거나 삼각형 메쉬를 구축하는 것과 같이 입자 위에 BVH를 구축하기 위한 많은 가능한 전략을 가능하게 한다. 이러한 전략에는 교점을 테스트하는 데 드는 비용과 경계의 견고성 사이에 trade-off가 있다. 예를 들어, 단순히 각 입자 주위의 AABB를 사용하여 광선을 교차시키는 것은 빠르지만 대각선으로 늘어난 Gaussian 입자로 인해 실제로 렌더링에 거의 영향을 주지 않는 많은 교점을 평가해야 한다. 이러한 전략들이 반드시 렌더링된 이미지에 영향을 미치지는 않지만, 계산 속도와 기여도가 낮은 불필요한 입자의 수에 영향을 미친다.
Stretched Polyhedron Proxy Geometry
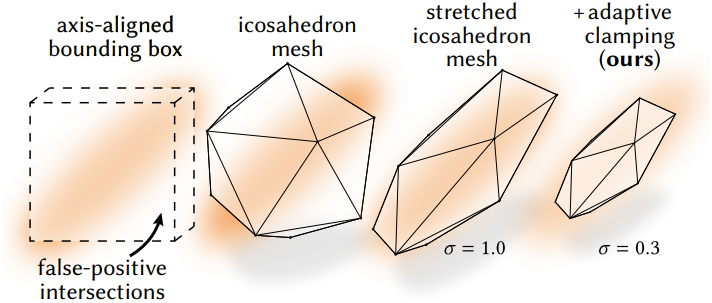
저자들은 많은 전략들을 실험한 결과, 입자의 경계를 잘 나타내고 하드웨어에 최적화된 광선-삼각형 교차의 이점을 제공하는 늘어난 정이십면체 메쉬에 입자를 사용하는 것이 가장 효과적이라는 것을 알아냈다. 경계 메쉬의 전면 삼각형에 대한 hit는 해당 입자가 처리되도록 한다. 캡처해야 하는 최소 response \(\alpha_\textrm{min}\)을 지정하여 (일반적으로 0.01) bounding proxy를 맞추고, 최소 \(\alpha_\textrm{min}\)으로 전체 공간을 덮기 위한 정이십면체의 크기를 조정한다. 각 입자에 대해 단위 내부 구를 갖는 정이십면체를 구성하고 다음과 같이 각 표준 꼭지점 $\mathbf{v}$를 변환한다.
중요한 것은 이 스케일링이 입자의 불투명도를 통합하므로 거의 투명한 큰 입자가 더 작은 bounding proxy를 가질 수 있어 입자의 적응형 clamping이 발생한다는 것이다.
2. Ray Tracing Renderer

입자에 대해 ray-casting할 수 있으면 렌더링을 위해서는 정렬된 순서로 광선을 따라 입자의 기여도를 누적해야 한다. NVIDIA OptiX 프로그래밍 모델을 사용하는 한 가지 단순한 접근 방식은 광선을 반복적으로 캐스팅하고 closest-hit 프로그램을 사용하여 가장 가까운 입자를 처리한 후 광선을 다시 캐스팅하여 다음 입자를 찾는 것이다. 또 다른 방법은 장면을 두 번만 횡단하는 것이다. 한 번은 투과율 함수를 추정하고, 한 번은 적분을 계산한다. 이 두 가지 전략 모두 장면을 통과하는 비용으로 인해 엄청나게 비용이 많이 든다.
본 논문의 renderer는 반투명 표면 또는 입자들을 tracing하기 위한 이전 접근 방식들을 기반으로 한다. Slab tracing은 particle slab를 반복적으로 수집하고 각 slab 내에서 정렬한다. Multi-layer alpha tracing은 모든 반투명 표면을 $k$-buffer로 처리하여 list가 overflow될 때 인접한 입자를 병합한다. 여러 근사로 인해 이러한 알고리즘들은 일관된 렌더링을 생성하지 못하여 미분 불가능하고 아티팩트를 생성한다.
알고리즘
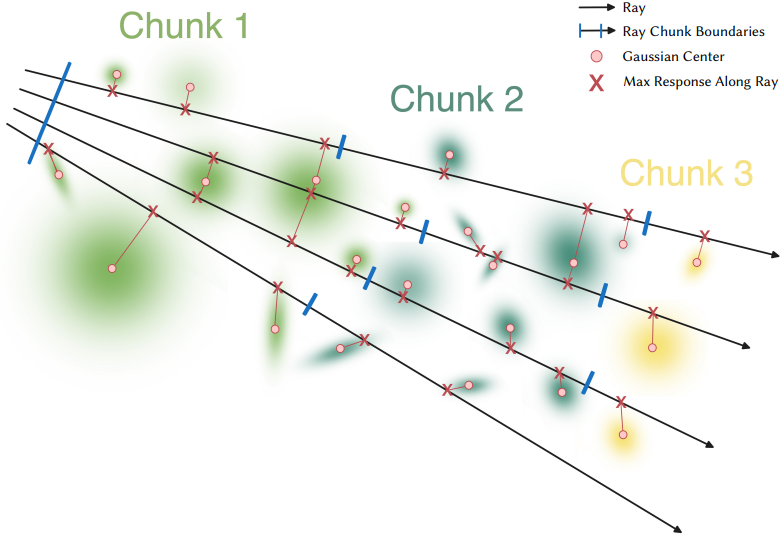
각 광선을 따라 들어오는 radiance를 계산하기 위해 ray-gen 프로그램은 BVH에 대해 ray tracing하여 다음 $k$개의 입자를 수집하며, any-hit 프로그램을 사용하여 입자들의 인덱스에 대한 정렬된 버퍼를 유지한다. 효율성을 위해 이 단계에서는 입자들의 response가 아직 평가되지 않으며, 모든 hit는 교차된 입자들로 처리된다. 그런 다음 ray-gen 프로그램은 정렬된 hit들에 대해 해당 입자를 검색하고 렌더링한다. 그런 다음 프로세스가 반복되어 마지막으로 렌더링된 입자에서 새로 ray tracing하여 다음 $k$개의 입자를 수집한다. 광선과 교차하는 모든 입자가 처리되면 프로세스가 종료되거나, 미리 정의된 최소 투과율 \(T_\textrm{min}\)에 도달할 만큼 밀도가 충분하면 즉시 조기 종료된다. 과거 접근 방식과 비교할 때 이 renderer는 입자를 누락하거나 투과율을 근사화하지 않고 일관된 순서로 교점을 처리할 수 있다.
이 제안된 알고리즘은 광범위한 벤치마킹 후 성능을 위해 선택된 많은 알고리즘 중 하나일 뿐이다. 알고리즘의 미묘한 변화는 dense하게 클러스터된 멀티뷰 장면에서 속도와 품질에 극적인 영향을 미친다.
3. 입자들의 response 평가
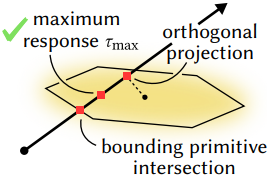
광선과 입자의 교점을 식별한 후에는 광선에 대한 각 입자의 기여도를 계산하는 방법을 선택해야 한다. 입자당 한 번 샘플링하지만 여전히 해당 샘플을 평가하기 위해 광선 위에서의 거리 $\tau$를 선택해야 한다.
Slab tracing은 입자의 중심을 광선에 직각으로 projection하였다. 이 전략은 등방성(isotropic) 입자에는 적합하지만 늘어난 이방성(anisotropic) 입자에는 오차가 발생할 수 있다. 대신, 저자들은 광선에서 입자가 최대 response를 가지는 지점인
\[\begin{equation} \tau_\textrm{max} = \textrm{argmax}_\tau \rho (\mathbf{o} + \tau \mathbf{d}) \end{equation}\]를 계산하였다. Gaussian 입자의 경우 \(\tau_\textrm{max}\)는 다음과 같다.
\[\begin{equation} \tau_\textrm{max} = \frac{(\boldsymbol{\mu} - \mathbf{o})^\top \boldsymbol{\Sigma}^{-1} \mathbf{d}}{\mathbf{d}^\top \boldsymbol{\Sigma}^{-1} \mathbf{d}} = \frac{- \mathbf{o}_g^\top \mathbf{d}_g}{\mathbf{d}_g^\top \mathbf{d}_g} \\ \textrm{where} \quad \mathbf{o}_g = \mathbf{S}^{-1} \mathbf{R}^\top (\mathbf{o} - \boldsymbol{\mu}), \quad \mathbf{d}_g = \mathbf{S}^{-1} \mathbf{R}^\top \mathbf{d} \end{equation}\]이 전략은 순서에서 약간의 근사치를 수반한다. 입자의 hit는 샘플 위치의 순서가 아닌 bounding primitive 교점의 순서로 통합된다. 그러나 이 근사치는 최종 결과의 품질에 실질적인 영향을 주지 않는다.
4. 미분 가능한 Ray Tracing 및 최적화
미분 가능한 렌더링


본 논문의 ray tracing renderer는 forward 렌더링 외에도 관찰된 데이터에서의 장면 최적화를 위해 미분 가능하다. 입자 파라미터와 관련하여 renderer를 통해 backpropagation하기 위해 먼저 forward-pass 렌더링을 수행하고 원하는 목적 함수를 계산한다. 그런 다음 backward pass에서 동일한 광선을 다시 캐스팅하여 동일한 입자들을 순서대로 샘플링하고 각 shading 표현에 대한 기울기를 계산하고 scatter-add 연산을 통해 공유 버퍼에 기울기를 축적한다. NVIDIA OptiX ray-gen 프로그램의 구조는 Procedure 1과 같다.
최적화
Ray tracer를 사용하여 입자 장면을 피팅하기 위해 pruning, cloning, splitting 연산을 포함한 3DGS의 최적화 방식을 채택한다. 3DGS는 cloning과 splitting의 기준으로 screen-space에서의 기울기를 추적하지만 보다 일반적인 설정에서는 screen-space에서의 기울기를 사용할 수 없거나 의미가 없다. 대신 3D world-space에서의 기울기를 사용한다. 또한 최적화 중에 입자가 업데이트되므로 ray tracing BVH를 정기적으로 재구성해야 한다.
불일치하는 광선을 사용한 학습
최적화는 각 iteration에서 무작위로 샘플링된 부분 집합에 피팅하는 stochastic descent의 이점을 누리는 경우가 많다. 그러나 미분 가능한 rasterization은 전체 이미지나 타일을 효율적으로 렌더링할 수만 있으므로 장면의 픽셀 집합에 대한 효율적인 stochastic한 최적화는 불가능하다. 본 논문의 ray tracer에서는 확률론적으로 샘플링된 광선을 사용하여 무작위로 또는 중요도 샘플링에 따라 자유롭게 학습할 수 있다. Stochastic sampling을 사용하는 경우 SSIM과 같은 window 기반 이미지 목적 함수를 사용할 수 없다.
5. Particle Kernel Functions

입자들이 Gaussian일 필요가 없으므로 다른 입자를 사용할 수 있다. 저자들은 Gaussian 외에도 kernel function $\hat{\rho} (\mathbf{x})$에 의해 정의된 세 가지 입자를 고려하였다.
- 3D Gaussians:
- Generalized Gaussians (degree = $n$, 저자들은 $n = 2$ 사용):
- Kernelized surfaces: 2D Gaussian Splatting과 같이 $z$축 scale이 없는 3D Gaussians
- Cosine wave modulations ($\psi$는 학습 가능한 파라미터):
Experiments
- 구현 디테일
- optimizer: Adam
- iteration: 30,000
- densification & pruning: 500 ~ 15,000
- learning rate: 3DGS와 동일
- 각 입자에서 카메라까지의 거리를 절반으로 스케일링한 3D world-space 기울기를 누적
- 최대 입자 수가 300만 개가 넘지 않도록 pruning
- densification 후 300만 개가 넘어가면 학습 뷰에서의 누적 가중치 기여도가 낮은 것들을 제거하여 270만개로 조절
- 학습 중에는 누적 투과도가 0.001 아래로 떨어지면 ray tracing을 종료
- inference 시에는 속도를 위해 threshold를 0.03으로 설정
- BVH는 매 iteration마다 업데이트, densification과 pruning 후에는 재구성
1. Novel View Synthesis
다음은 다른 novel view synthesis 방법들과 비교한 결과이다.

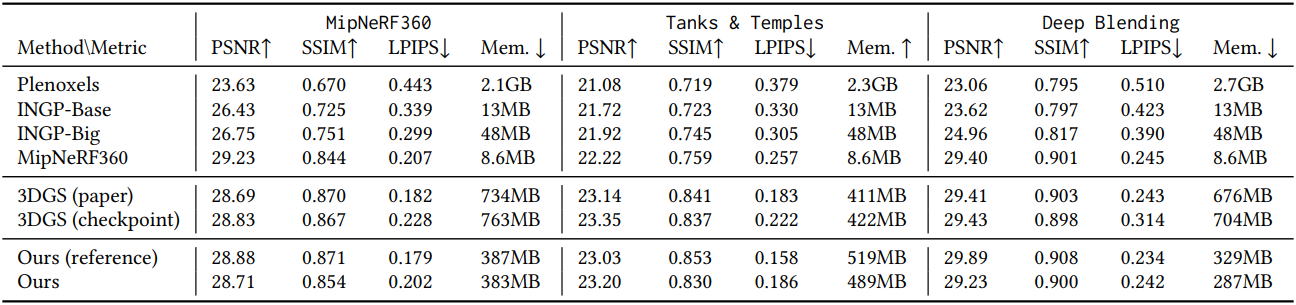
다음은 3DGS와 FPS를 비교한 표이다.

2. Ray Tracing 분석 및 Ablations
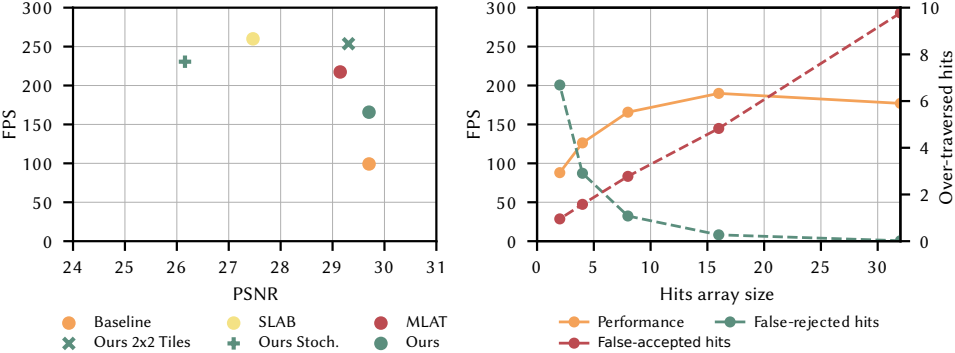
다음은 (왼쪽) tracing 알고리즘과 (오른쪽) hit buffer size에 대한 ablation 결과이다.
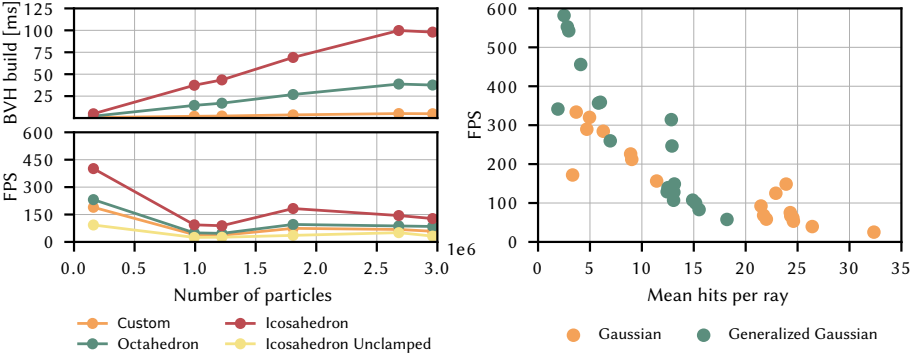
다음은 (왼쪽) primitive에 대한 ablation 결과와 (오른쪽) 평균 hit 수에 따른 FPS를 비교한 그래프이다.
다음은 kernel function에 따른 hit 수를 시각화한 것이다. 왼쪽은 3D Gaussian이고 오른쪽은 Generalized Gaussian을 사용한 결과이다.

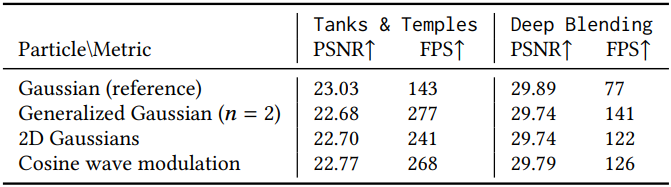
다음은 kernel function에 따른 렌더링 품질과 속도 사이의 trade-off를 비교한 표이다.
3. 상호 운용성
다음은 사전 학습된 3DGS를 fine-tuning한 결과이다.

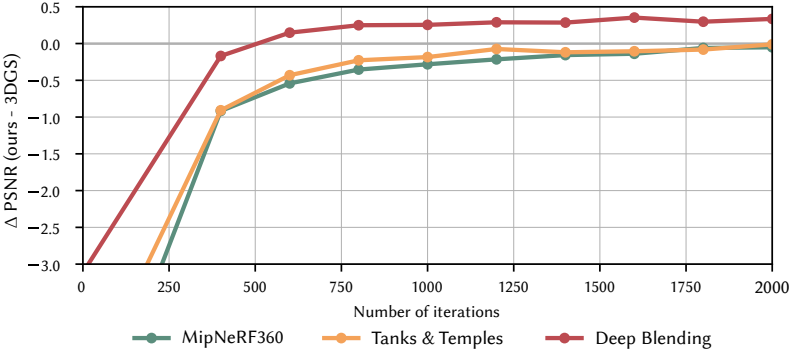
Applications
1. 광선 기반 효과
다음은 (왼쪽 위) 반사, (가운데 위) depth of field, (왼쪽 아래) 굴절, (가운데 아래) 그림자, 그리고 (오른쪽) 이것들의 조합의 예시이다.

다음은 ray tracing 특성을 통해 광선을 반사 및 굴절하고, 그림자를 만들고, 카메라 효과를 적용한 결과이다.

2. Instancing
다음은 Tank & Temples 트럭 1024개를 렌더링한 예시이다. (FPS는 25 이상)

3. Denoising & Stochastic Sampling
다음은 stochastic sampling의 예시이다. 왼쪽부터 3DGRT로 렌더링한 장면, stochastic sampling으로 렌더링한 장면 (샘플 4개), NVIDIA OptiX denoiser로 denoising한 결과이다.

4. 복잡한 카메라 및 자율주행 장면
다음은 (a) fisheye 입력으로 재구성한 예시와 (b) 롤링 셔터 효과를 보정한 예시이다.


다음은 현실 자율주행 장면에 대한 재구성 결과이다.
