[논문리뷰] 3D Gaussian Splatting for Real-Time Radiance Field Rendering
SIGGRAPH 2023. [Paper] [Page] [Github]
Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, George Drettakis
Inria | Max-Planck-Institut für Informatik
8 Aug 2023
Introduction
메쉬와 포인트는 명시적이며 빠른 GPU/CUDA 기반 rasterization에 적합하기 때문에 가장 일반적인 3D 장면 표현이다. 대조적으로, 최근 NeRF는 연속적인 장면 표현을 기반으로 하며 일반적으로 캡처된 장면의 새로운 뷰 합성을 위해 volumetric ray-marching을 사용하여 MLP를 최적화한다. 마찬가지로, 현재까지 가장 효율적인 radiance field 솔루션은 복셀이나 해시 그리드 또는 포인트에 저장된 값을 보간하여 연속 표현을 기반으로 구축된다. 이러한 방법들의 특성은 최적화에 도움이 되지만, 렌더링에 필요한 확률론적 샘플링에는 비용이 많이 들고 잡음이 발생할 수 있다. 본 논문은 두 세계의 장점을 결합한 새로운 접근 방식을 소개하였다. 3D Gaussian 표현을 통해 SOTA 시각적 품질과 경쟁력 있는 학습 시간으로 최적화할 수 있으며, 타일 기반 splatting 솔루션은 1080p 해상도에서의 SOTA 품질의 실시간 렌더링을 보장한다.
본 논문의 목표는 여러 사진으로 캡처한 장면에 대해 실시간으로 렌더링하고 일반적인 실제 장면에 대해 가장 효율적인 이전 방법만큼 빠르게 최적화 시간으로 표현을 생성하는 것이다. 최근 방법들은 빠른 학습을 달성하지만 최대 48시간의 학습 시간이 필요한 현재 SOTA NeRF 방법, 즉 Mip-NeRF360으로 얻은 시각적 품질을 달성하는 데 어려움을 겪는다. 빠르지만 품질이 낮은 radiance field 방법은 장면에 따라 인터랙티브한 렌더링 시간 (초당 10~15 프레임)을 달성할 수 있지만 고해상도의 실시간 렌더링에는 미치지 못한다.
본 논문의 솔루션은 세 가지 주요 구성 요소를 기반으로 한다. 먼저 유연하고 표현력이 풍부한 장면 표현으로 3D Gaussian을 소개한다. 이전 NeRF와 유사한 방법, 즉 SfM(Structure-from-Motion)으로 보정된 카메라와 동일한 입력으로 시작하고 SfM 프로세스의 일부로 생성된 sparse한 포인트 클라우드로 3D Gaussian 집합을 초기화한다. Multi-View Stereo (MVS) 데이터가 필요한 대부분의 포인트 기반 솔루션과 달리 SfM 포인트만 입력하여 고품질 결과를 얻는다. NeRF 합성 데이터셋의 경우, 랜덤 초기화를 통해서도 높은 품질을 달성한다. 3D Gaussian은 미분 가능한 체적 표현이기 때문에 탁월한 선택이다. 그러나 2D로 투영하고 NeRF와 동등한 이미지 형성 모델을 사용하여 표준 $\alpha$-블렌딩을 적용하여 매우 효율적으로 rasterization할 수도 있다.
두 번째 구성 요소는 3D 위치, 불투명도 $\alpha$, 이방성 공분산, 구면 조화 (SH) 계수와 같은 3D Gaussian의 속성을 최적화하는 것이다. 이는 적응형 밀도 제어 단계와 인터리브되어 최적화 중에 3D Gaussian을 추가하거나 때때로 제거한다. 최적화 절차는 장면을 합리적으로 간결하고 구조화되지 않은 정확한 표현으로 생성한다.
마지막 구성 요소는 빠른 GPU 정렬 알고리즘을 사용하고 타일 기반 rasterization에서 영감을 얻은 실시간 렌더링 솔루션이다. 그러나 3D Gaussian 표현 덕분에 가시성(visibility) 순서를 존중하는 이방성 splatting을 수행할 수 있으며, 필요한 만큼 정렬된 splat의 순회(traversal)를 추적하여 빠르고 정확한 backward pass가 가능하다.
3D Gaussian Splatting은 멀티뷰 캡처에서 3D Gaussian을 최적화하고 이전의 암시적 radiance field 접근 방식의 최고 품질과 동일하거나 더 나은 품질을 달성할 수 있다. 또한 가장 빠른 방법과 유사한 학습 속도와 품질을 달성할 수 있으며 중요한 것은 새로운 뷰 합성을 위한 고품질의 최초 실시간 렌더링을 제공한다는 것이다.
Differentiable 3D Gaussian Splatting

본 논문의 목표는 법선이 없는 sparse한 SfM 점 집합에서 시작하여 고품질의 새로운 뷰를 합성하는 장면 표현을 최적화하는 것이다. 이를 위해서는 미분 가능한 체적 표현의 속성을 상속하는 동시에 매우 빠른 렌더링이 가능하도록 구조화되지 않고 명시적인 기본 요소가 필요하다. 저자들은 미분 가능하고 2D splat으로 쉽게 투영할 수 있는 3D Gaussian을 선택하여 렌더링을 위한 빠른 $\alpha$-블렌딩이 가능하도록 하였다.
표현은 2D 점을 사용하고 각 점이 법선이 있는 작은 평면 원이라고 가정하는 이전 방법과 유사하다. SfM 점의 극도의 희박성(sparsity)을 고려하면 법선을 추정하는 것은 매우 어렵다. 마찬가지로, 그러한 추정으로부터 잡음이 많은 법선을 최적화하는 것은 매우 어려울 것이다. 그 대신 법선이 필요하지 않은 3D Gaussian 집합으로 형상을 모델링한다. Gaussian은 점 평균 $\mu$를 중심으로 한 world space에 정의된 3D 공분산 행렬 $\Sigma$로 정의된다.
\[\begin{equation} G(x) = e^{-\frac{1}{2} x^\top \Sigma^{-1} x} \end{equation}\]이 Gaussian은 블렌딩 과정에서 $\alpha$로 곱해진다.
그러나 렌더링을 위해서는 3D Gaussian을 2D로 투영해야 한다. 뷰 변환 $W$가 주어지면 카메라 좌표의 공분산 행렬 $\Sigma^\prime$은 다음과 같다.
\[\begin{equation} \Sigma^\prime = J W \Sigma W^\top J^\top \end{equation}\]여기서 $J$는 projection 변환의 affine 근사의 Jacobian이다. 또한 $\Sigma^\prime$의 세 번째 행과 열을 제거하면 법선이 있는 평면 점에서 시작하는 것과 동일한 구조와 속성을 가진 2$\times$2 분산 행렬을 얻을 수 있다.
분명한 접근법은 공분산 행렬 $\Sigma$를 직접 최적화하여 radiance field를 나타내는 3D Gaussian을 얻는 것이다. 그러나 공분산 행렬은 positive semi-definite인 경우에만 물리적인 의미를 갖는다. 모든 파라미터의 최적화를 위해 유효한 행렬을 생성하도록 쉽게 제한할 수 없는 경사 하강법(gradient descent)을 사용하며, 업데이트 단계와 경사는 매우 쉽게 유효하지 않은 공분산 행렬을 생성할 수 있다.
결과적으로 저자들은 최적화를 위해 보다 직관적이면서도 표현력이 뛰어난 표현을 선택했다. 3D Gaussian의 공분산 행렬 $\Sigma$는 타원체의 구성을 설명하는 것과 유사하다. 스케일링 행렬 $S$와 회전 행렬 $R$이 주어지면 $\Sigma$를 찾을 수 있다.
\[\begin{equation} \Sigma = R S S^\top R^\top \end{equation}\]두 요소를 독립적으로 최적화할 수 있도록 스케일링을 위한 3D 벡터 $s$와 회전을 나타내는 quaternion $q$를 별도로 저장한다. 이들은 각각의 행렬로 간단하게 변환되고 결합될 수 있으며, $q$를 정규화하여 유효한 단위 quaternion을 얻을 수 있다. 학습 중 자동 미분으로 인한 상당한 오버헤드를 피하기 위해 모든 파라미터에 대한 기울기를 명시적으로 도출한다. 최적화에 적합한 이방성 공분산 표현을 통해 3D Gaussian을 최적화하여 캡처된 장면의 다양한 모양의 기하학적 구조에 적응할 수 있으므로 상당히 컴팩트한 표현이 가능해진다. 그림 3은 그러한 케이스들을 보여준다.

Optimization with Adaptive Density Control of 3D Gaussians
본 논문의 접근 방식의 핵심은 프리뷰 합성을 위해 장면을 정확하게 표현하는 dense한 3D Gaussian 집합을 생성하는 최적화 단계이다. 위치 $p$, $\alpha$, 공분산 $\Sigma$ 외에도 각 Gaussian의 색상 $c$를 나타내는 SH 계수를 최적화하여 뷰에 따른 장면의 모양을 올바르게 캡처한다. 이러한 파라미터의 최적화는 장면을 더 잘 표현하기 위해 Gaussian의 밀도를 제어하는 단계와 인터리브된다.
1. Optimization
최적화는 렌더링의 연속적인 반복을 기반으로 하며 결과 이미지를 캡처된 데이터셋의 학습 뷰와 비교한다. 필연적으로 3D에서 2D로의 투영이 모호하기 때문에 형상이 잘못 배치될 수 있다. 따라서 최적화는 형상을 생성하고 형상이 잘못 배치된 경우 형상을 파괴하거나 이동할 수 있어야 한다. 3D Gaussian의 공분산 파라미터의 품질은 소수의 큰 이방성 Gaussian을 사용하여 큰 homogeneous 영역을 캡처할 수 있으므로 표현을 간결하게 하는 데 중요하다.
표준 GPU 가속 프레임워크를 최대한 활용하고 일부 연산에 커스텀 CUDA 커널을 추가하는 기능을 활용하기 위해 최적화에 stochastic gradient descent (SGD)를 사용한다. 특히 fast rasterization는 최적화의 주요 계산상의 병목 현상이기 때문에 최적화 효율성에 매우 중요하다.
저자들은 $\alpha$에 sigmoid activation function를 사용하여 $[0, 1)$에서 제한하고 부드러운 기울기를 얻었으며, 비슷한 이유로 공분산의 스케일에 대한 exponential activation function를 사용했다.
초기 공분산 행렬은 가장 가까운 세 점까지의 거리 평균과 동일한 축을 갖는 등방성 Gaussian으로 추정된다. Plenoxels와 유사한 표준 exponential decay 스케줄링 기술을 사용하지만 위치에만 적용된다. Loss function은 D-SSIM 항과 결합된 \(\mathcal{L}_1\)이다.
\[\begin{equation} \mathcal{L} = (1 - \lambda) \mathcal{L}_1 + \lambda \mathcal{L}_\textrm{D-SSIM} \end{equation}\]저자들은 모든 테스트에서 $\lambda = 0.2$를 사용하였다.
2. Adaptive Control of Gaussians
SfM의 초기 sparse한 포인트 집합에서 시작한 다음 Gaussian 수와 단위 볼륨에 대한 밀도를 적응적으로 제어하는 방법을 적용하여 초기 sparse한 Gaussian 집합에서 장면을 더 잘 나타내는 더 dense한 집합으로 이동할 수 있다. 최적화 warm-up 후 매 100 iteration마다 densify하고 본질적으로 투명한 Gaussian, 즉 threshold $\epsilon_\alpha$보다 작은 $\alpha$를 제거한다.
Gaussian에 대한 적응형 제어는 빈 영역을 채워야 한다. 기하학적 feature가 누락된 영역 (“under-reconstruction”)에 초점을 맞추지만 Gaussian이 장면에서 넓은 영역을 덮는 영역 (“over-reconstruction”)에도 중점을 둔다. 둘 다 큰 view space 위치 기울기를 가지고 있다. 직관적으로 이는 아직 잘 재구성되지 않은 영역에 해당하고 최적화에서는 이를 수정하기 위해 Gaussian을 이동하려고 하기 때문일 가능성이 높다. 두 경우 모두 densification을 위한 좋은 후보이므로 저자들은 테스트에서 0.0002로 설정한 threshold \(\tau_\textrm{pos}\) 이상의 view space 위치 기울기의 평균 크기를 사용하여 Gaussian을 densify한다.
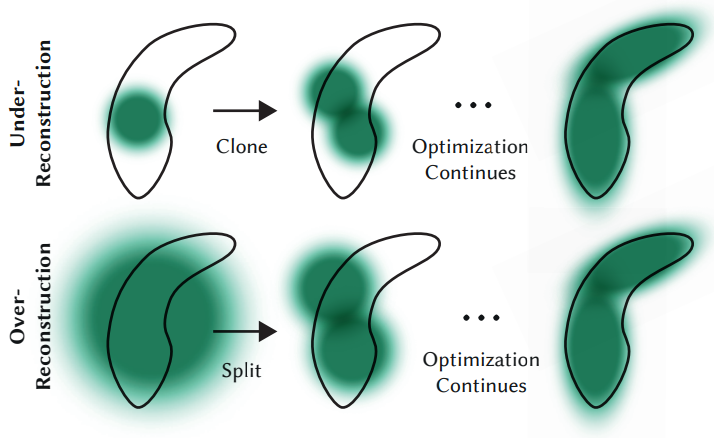
재구성되지 않은 영역에 있는 작은 Gaussian의 경우 생성해야 하는 새로운 형상을 처리해야 한다. 이를 위해 동일한 크기의 복사본을 만들고 이를 위치 기울기 방향으로 이동하여 Gaussian을 복제하는 것이 좋다.
반면, 분산이 높은 지역의 큰 Gaussian은 더 작은 Gaussian으로 분할되어야 한다. 이러한 Gaussian들은 두 개의 새로운 Gaussian으로 대체하고 실험적으로 결정한 $\phi = 1.6$로 나눈다. 또한 원본 3D Gaussian을 샘플링용 PDF로 사용하여 위치를 초기화한다.
첫 번째 경우에는 시스템의 총 부피와 Gaussian 수를 모두 늘려야 하는 필요성을 감지하고 처리하는 반면, 두 번째 경우에는 총 부피를 보존하지만 Gaussian 수를 늘린다. 다른 체적 표현과 마찬가지로 최적화는 입력 카메라에 가까운 floater들로 인해 정체될 수 있으며, 본 논문의 경우에는 Gaussian 밀도가 정당하지 않게 증가할 수 있다. Gaussian 수의 증가를 조절하는 효과적인 방법은 $N = 3000$회 반복마다 $\alpha$ 값을 0에 가깝게 설정하는 것이다. 그런 다음 최적화는 위에서 설명한 대로 $\epsilon_\alpha$보다 작은 $\alpha$의 Gaussian을 제거하는 방식을 사용하여 Gaussian에 대한 $\alpha$를 증가시킨다. Gaussian은 축소되거나 커질 수 있으며 다른 것드과 상당히 겹칠 수 있지만, world space에서 매우 큰 Gaussian과 view space에서 차지하는 공간이 큰 Gaussian을 주기적으로 제거한다. 이 전략을 사용하면 총 Gaussian 수를 전반적으로 효과적으로 제어할 수 있다. 모델의 Gaussian은 항상 유클리드 공간에서 기본 요소로 유지된다. 다른 방법과 달리 멀리 있거나 큰 Gaussian에 대한 공간 압축, 워핑 또는 투영 전략이 필요하지 않다.

Fast Differentiable Rasterizer for Gaussians
본 논문의 목표는 대략적인 $\alpha$-blending을 허용하고 기울기를 받을 수 있는 splat 수에 대한 엄격한 제한을 피하기 위해 빠른 전체 렌더링과 빠른 정렬을 갖는 것이다.
이러한 목표를 달성하기 위해 저자들은 이전 $\alpha$-blending 솔루션을 방해했던 픽셀당 정렬의 비용을 피하면서 한 번에 전체 이미지에 대해 기초 요소를 사전 정렬하는 최근 소프트웨어 rasterization 방식에서 영감을 받은 Gaussian splat용 타일 기반 rasterizer를 설계하였다. 이 고속 rasterizer는 임의의 수의 혼합된 Gaussian에 대한 효율적인 역전파가 가능하며, 추가 메모리 소비가 적고 픽셀당 일정한 오버헤드만 필요로 한다. 본 논문의 rasterization 파이프라인은 완전히 미분 가능하며 2D로의 투영을 고려하면 이전 2D splattng 방법과 유사한 이방성 splat을 rasterization할 수 있다.
본 논문의 방법은 화면을 16$\times$16 타일로 분할하는 것으로 시작한다. 그런 다음 view frustum과 각 타일에 대해 3D Gaussian을 선별하는 것으로 진행된다. 구체적으로 view frustum과 교차하는 99% 신뢰 구간의 Gaussian만 유지한다. 추가적으로, 투영된 2D 공분산 계산이 불안정할 수 있기 때문에 guard band를 사용하여 극단적인 위치를 거부한다. 그런 다음 겹치는 타일 수에 따라 각 Gaussian을 인스턴스화하고 각 인스턴스에 view space 깊이와 타일 ID를 결합하는 key를 할당한다. 그런 다음 단일 고속 GPU Radix sort를 사용하여 이러한 key를 기반으로 Gaussian을 정렬한다. 추가적인 픽셀별 포인트 순서는 없으며 블렌딩은 이 초기 정렬을 기반으로 수행된다. 결과적으로 본 논문의 $\alpha$-blending은 일부 구성에서 근사치일 수 있다. 그러나 splat이 개별 픽셀 크기에 가까워지면 이러한 근사값은 무시할 수 있다. 저자들은 이 선택이 수렴된 장면에서 눈에 보이는 아티팩트를 생성하지 않고 학습 및 렌더링 성능을 크게 향상시킨다는 것을 발견했다.
Gaussian을 정렬한 후 주어진 타일에 표시되는 첫 번째 및 마지막 entry를 식별하여 각 타일에 대한 list를 생성한다. Rasterization를 위해 각 타일에 대해 하나의 스레드 블록을 실행한다. 각 블록은 먼저 Gaussian의 패킷을 공유 메모리에 공동으로 로드한 다음 지정된 픽셀에 대해 list를 앞뒤로 순회하여 색상과 $\alpha$ 값을 누적하므로 데이터 로드/공유 및 처리 모두에 대한 병렬 처리의 이득을 최대화한다. 픽셀에서 타겟 채도 $\alpha$에 도달하면 해당 스레드가 중지된다. 정기적으로 타일의 스레드가 쿼리되고 모든 픽셀이 포화되면, 즉 $\alpha$가 1에 가까워지면 전체 타일의 처리가 종료된다. 정
Rasterization 중에는 $\alpha$의 채도가 유일한 중지 기준이다. 이전 연구들과 달리 기울기 업데이트를 받는 혼합된 기본 요소의 수를 제한하지 않는다. 저자들은 이 속성을 적용하여 장면별 하이퍼파라미터 튜닝에 의존하지 않고도 임의적이고 다양한 깊이의 복잡성이 있는 장면을 처리하고 정확하게 학습할 수 있도록 하였다. 따라서 backward pass 동안 forward pass에서 픽셀당 혼합된 포인트의 전체 시퀀스를 복구해야 한다. 한 가지 해결책은 글로벌 메모리에 픽셀당 혼합된 포인트의 임의의 긴 list를 저장하는 것이다. 대신에 저자들은 동적 메모리 관리 오버헤드를 피하기 위해 타일별 list를 다시 탐색하도록 선택하였다. Forward pass에서 정렬된 Gaussian의 array와 타일 range를 재사용할 수 있다. 기울기 계산을 용이하게 하기 위해 이제 뒤에서 앞으로 순회한다.
순회는 타일의 모든 픽셀에 영향을 준 마지막 지점부터 시작되며 공유 메모리에 포인트를 다시 로드하는 작업이 공동으로 수행된다. 또한 각 픽셀은 forward pass 중에 해당 색상에 기여한 마지막 포인트의 깊이보다 깊이가 낮거나 같은 경우에만 오버랩 테스트와 포인트 처리를 시작한다. 기울기 계산 시에는 원본 블렌딩 프로세스 중 각 step에서 누적된 불투명도 값이 필요하다. Backward pass에서 점진적으로 줄어드는 불투명도의 list를 순회하는 대신 forward pass가 끝날 때 누적된 총 불투명도만 저장하여 이러한 중간 불투명도를 복구할 수 있다. 특히 각 포인트는 forward 프로세스에서 최종 누적 불투명도 $\alpha$를 저장한다. 이를 뒤에서 앞으로 순회할 때 각 포인트의 $\alpha$로 나누어 기울기 계산에 필요한 계수를 얻는다.

Experiments
1. Results and Evaluation
다음은 이전 연구들과 본 논문의 방법을 정량적으로 비교한 표이다.

다음은 iteration에 따른 시각적 결과들이다.

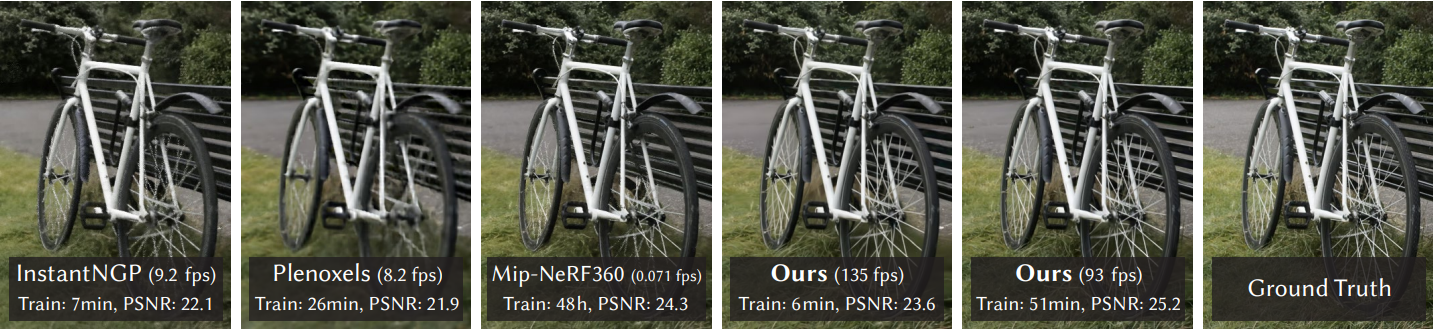
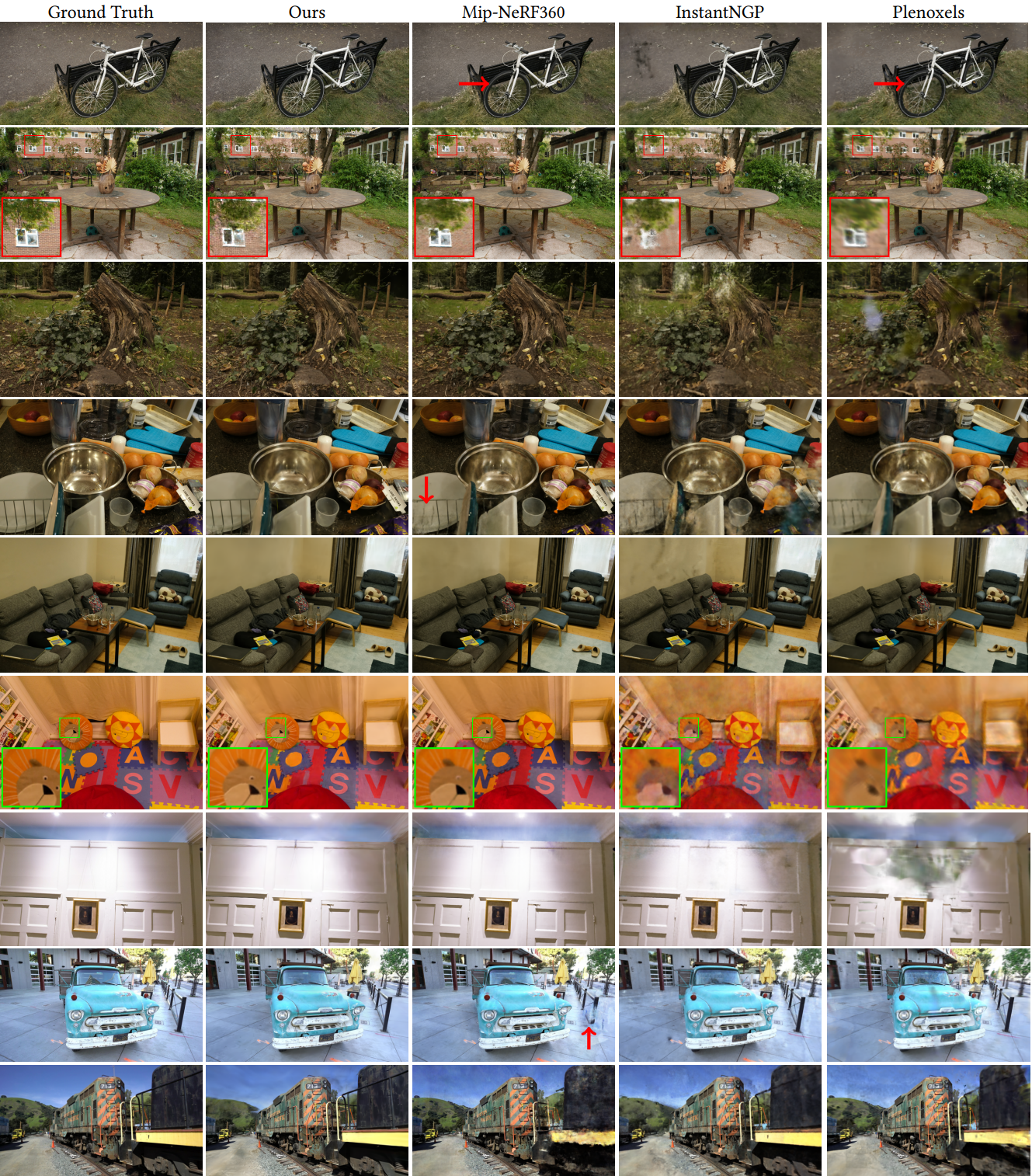
다음은 이전 연구들과 본 논문의 방법을 시각적으로 비교한 것이다.
다음은 Synthetic NeRF에서의 PSNR 점수이다.

2. Ablations
다음은 ablation study의 PSNR 점수이다.

다음은 SfM으로 초기화하는 것에 대한 ablation 결과이다.

다음은 densification 전략에 대한 ablation 결과이다.

다음은 기울기를 받는 포인트의 수에 대한 ablation 결과이다. 왼쪽은 기울기를 받는 Gaussian을 10개로 제한한 것이고 오른쪽은 본 논문의 방법이다.

다음은 Gaussian 이방성을 비활성화하고 장면을 학습한 결과와 활성화하고 장면을 학습한 결과를 비교한 것이다.

3. Limitations

다른 방법들과 마찬가지로 장면이 잘 관찰되지 않는 지역에는 아티팩트가 있다. 위 그림은 아티팩트를 비교한 것으로, 왼쪽은 Mip-NeRF360, 오른쪽은 본 논문의 방법이다.

또한 학습 중에 본 뷰와 거의 겹치지 않는 뷰에서 아티팩트를 생성할 수 있다. 왼쪽은 Mip-NeRF360, 오른쪽은 본 논문의 방법이다.