[논문리뷰] 2D-Guided 3D Gaussian Segmentation
arXiv 2023. [Paper]
Kun Lan, Haoran Li, Haolin Shi, Wenjun Wu, Yong Liao, Lin Wang, Pengyuan Zhou
University of Science and Technology of China | HKUST
26 Dec 2023
Introduction
최근 등장한 3D Gaussian 기술은 포인트 클라우드, 메쉬, signed distance function (SDF), NeRF와 같은 이전 3D 표현 방법에 비해 특히 학습 시간 및 장면 재구성 품질 측면에서 상당한 발전을 이루었다. 각 3D Gaussian의 평균은 중심점의 위치를 나타내고, 공분산 행렬은 회전과 크기를 나타내며, spherical harmonics는 색상을 나타낸다. SFM에서 얻은 포인트 클라우드부터 시작하여 3D Gaussian들은 본질적으로 장면의 기하학적 정보를 포함하므로 공간에서 개체가 있는 영역을 찾는 시간을 절약한다. 또한 명시적인 표현 방법을 통해 공간의 모든 3D Gaussian에 대한 색상 및 밀도 계산을 더욱 가속화하여 실시간 렌더링이 가능하며, 적응형 밀도 제어를 통해 세부적인 특징을 표현할 수 있는 능력을 가진다. 이러한 장점으로 인해 3D 이해 및 편집에 널리 적용할 수 있다. 그럼에도 불구하고, 이 영역의 또 다른 중요한 기둥인 3D Gaussian segmentation에 대한 연구는 거의 없다.
최근 몇 가지 Gaussian segmentation 방법이 제안되었으나 추가 개선이 필요하다. 예를 들어 Gaussian Grouping에는 약 15분의 추가 학습이 필요하다. SAGA는 구현이 복잡하고 여러 개체를 동시에 분할하는 데 어려움을 겪는다. 또한 3D Gaussian들을 명시적으로 표현하면 저장 오버헤드가 발생하여 NeRF segmentation에서와 같이 2D semantic feature들을 3D로 직접 전송할 수 없다. 마지막으로, 데이터셋의 부족으로 인해 2D 및 포인트 클라우드 segmentation에 일반적으로 사용되는 supervised segmentation 방법의 적용이 힘들다.
본 논문은 앞서 언급한 문제를 고려하여 사전 학습된 2D segmentation 모델을 활용하여 3D Gaussian segmentation을 가이드할 것을 제안하였다. 서로 다른 카테고리에 걸쳐 각 픽셀에 확률 분포 벡터를 할당하는 2D segmentation 접근 방식에서 영감을 받아 먼저 각 3D Gaussian에 object code를 할당하여 Gaussian의 카테고리형 확률 분포를 나타낸다. 이어서, 주어진 포즈에서 2D segmentation map과 렌더링된 segmentation map 간의 오차를 최소화하여 각 3D Gaussian의 분류를 가이드하는 알고리즘을 사용한다. 마지막으로 KNN clustering을 사용하여 3D Gaussian의 semantic 모호성을 해결하고 통계적 필터링을 사용하여 잘못 분할된 3D Gaussian들을 제거한다.
Method
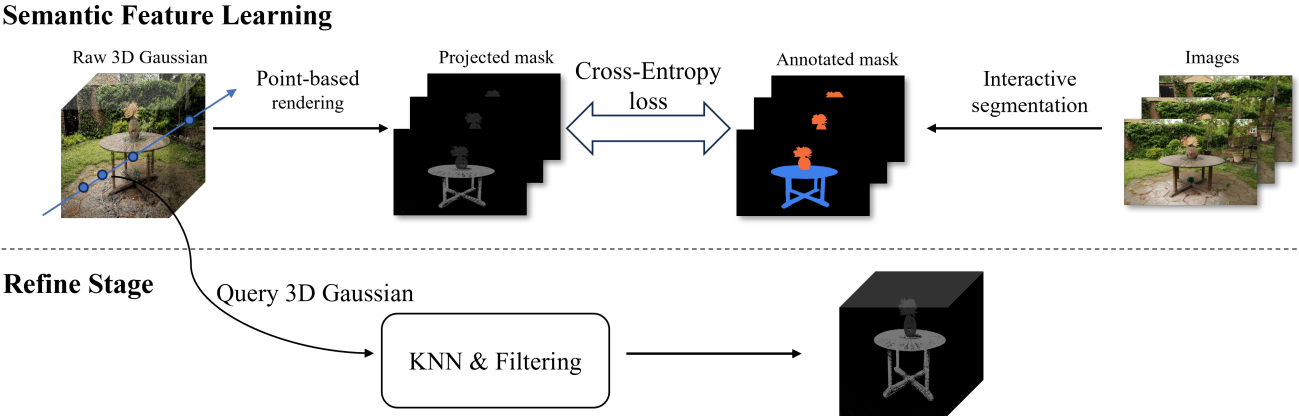
3D Gaussian 표현, 장면 렌더링 이미지, 카메라 파라미터를 사용하여 잘 학습된 장면이 주어지면 처음에는 렌더링된 이미지를 분할하기 위해 대화형 2D segmentation 모델을 사용한다. 그런 다음 획득된 2D segmentation map은 3D Gaussian에 추가된 semantic(object code)의 학습을 용이하게 하기 위한 guidance로 사용된다. 마지막으로 KNN clustering을 사용하여 특정 3D Gaussian의 semantic 모호성 문제를 해결하고, 선택적인 통계적 필터링을 사용하면 잘못 분할된 3D Gaussian들을 제거하는 데 도움이 될 수 있다. 파이프라인은 위 그림에 나와 있다.
1. Point-Based rendering and Semantic Information Learning
Gaussian Splatting은 포인트 기반 렌더링 기술($\alpha$-블렌딩)을 사용하여 3D 장면을 평면에 렌더링하며 평면의 픽셀 색상은 다음과 같이 계산할 수 있다.
\[\begin{equation} C = \sum_{i \in \mathcal{N}} c_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]여기서 $\mathcal{N}$은 픽셀과 겹치는 정렬된 Gaussian들을 나타내고, $c_i$는 현재 픽셀에 투영된 각 3D Gaussian의 색상을 나타내며, $\alpha_i$는 공분산 $\Sigma$와 학습된 Gaussian별 불투명도를 곱하여 2D Gaussian들을 평가하여 제공된다. $\alpha$는 투영된 2D Gaussian 중심으로부터의 거리가 증가함에 따라 감소하는 투영된 2D Gaussian의 모든 점의 불투명도를 표현한다는 점에 주목할 가치가 있다.
3D 장면을 분할하려면 semantic 정보를 장면 표현에 통합해야 한다. 2D segmentation에서 영감을 받아 각 3D Gaussian에 object code $\mathbf{o} \in \mathbb{R}^K$를 할당하여 다양한 카테고리에 걸쳐 현재 3D Gaussian의 확률 분포를 나타낸다. 여기서 $K$는 카테고리 수이다. $\mathbf{o}$의 첫 번째 차원은 배경 클래스이다.
추가된 3D semantic 정보를 학습하기 위한 supervision으로 2D segmentation map을 사용하려면 추가된 semantic 정보를 3D에서 2D 평면에 투영해야 한다. $\alpha$-블렌딩에서 영감을 받아 렌더링된 2D segmentation map의 픽셀 카테고리를 렌더링 중 현재 광선을 따라 있는 여러 3D Gaussian 카테고리의 가중치 합으로 간주한다. 저자들은 첫 번째 3D Gaussian이 가장 많은 기여를 한다고 가정하였으며, 이후의 각 3D Gaussian의 기여도는 렌더링 평면으로부터의 거리에 따라 감소하며, 이 기여도는 3D Gaussian 자체의 크기에 비례한다. 렌더링된 이미지의 각 픽셀 카테고리는 3D Gaussian의 object code로 다음과 같이 나타낼 수 있다.
\[\begin{equation} \hat{\mathbf{o}} = \sum_{i \in \mathcal{N}} o_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]이는 $\alpha$-블렌딩 식에서 각 3D Gaussian의 색상 $c$를 각 3D Gaussian의 object code로 대체한 것이다.
2D ground truth 레이블에 해당하는 $L$개의 이미지
\[\begin{equation} \{I_1, \cdots, I_l, \cdots, I_L\}, \quad I_l \in \mathbb{R}^{H \times W} \end{equation}\]가 있다고 가정하자. 여기서 $L$은 데이터셋의 카메라 포즈 수이고, $H$와 $W$는 각각 레이블의 높이와 너비이다. Ground-truth 레이블의 각 요소는 해당 픽셀의 카테고리 레이블을 나타낸다. 그런 다음 ground truth와 동일한 카메라 시점에서 $L$개의 투영된 segmentation map
\[\begin{equation} \{\bar{I}_1, \cdots, \bar{I}_l, \cdots, \bar{I}_L\}, \quad \bar{I}_l \in \mathbb{R}^{K \times H \times W} \end{equation}\]를 생성한다. 이러한 투영된 segmentation map에서 각 요소는 $i$번째 카테고리에 속하는 픽셀의 확률을 나타낸다. ($i = 1, 2, \cdots, K$)
다음으로, 원래의 2D segmentation map은 one-hot 벡터로 변환된 후 $M \in \mathbb{R}^{K \times N}$으로 reshape된다. 여기서 $N = H \times W$이다. 투영된 segmentation map과 유사한 연산을 수행하여 $\bar{M} \in \mathbb{R}^{K \times N}$을 얻는다. 그런 다음 ground truth 객체 마스크 $M$과 투영된 객체 마스크 $\bar{M}$을 사용하여 Cross-Entropy Loss(CES)를 계산한다.
\[\begin{equation} L_i = - \frac{1}{N} \sum_{n=1}^N M_i^n \log \bar{M}_i^n, \quad 0 \le i < K \end{equation}\]최종 loss는은 $L$개의 이미지 쌍에 대한 모든 loss의 평균이다.
\[\begin{equation} \mathcal{L} = \frac{1}{L} \sum_{l=1}^L \textrm{CES}_l, \quad \textrm{where} \; \textrm{CES}_l = \frac{1}{K} \sum_{i=1}^K L_i \end{equation}\]2. Gaussian Clustering
저자들은 실험 중에 3D semantic 정보를 학습하기 위한 유일한 가이드로 2D segmentation map을 사용하면 일부 3D Gaussian의 semantic 정보가 부정확해질 수 있음을 관찰했다. 이러한 부정확성은 모든 카테고리에 걸쳐 초기 균일 분포 상태에 근접한 3D Gaussian으로 나타나거나 제한된 수의 카테고리에서 유사한 확률을 나타낸다. 이 문제를 해결하고 물체가 공간에 지속적으로 분산된다는 점을 고려하여 각 3D Gaussian은 일반적으로 특정 proximity(근접성)에 위치한 다른 3D Gaussian과 동일한 카테고리 내에서 분류되어야 한다고 가정하였다.
저자들은 semantic 정보의 부정확성을 해결하기 위해 KNN clustering 알고리즘을 참조하였다. 사전 학습된 semantic 정보가 있는 3D 장면의 경우 장면을 표현하는 데 사용되는 각 3D Gaussian의 object code $\mathbf{o}$를 처음에 검색한다. 그런 다음 이러한 code는 softmax 처리를 거쳐 다양한 카테고리에 걸쳐 각 3D Gaussian의 확률 분포를 추론한다. 확률의 최대값 $\max (sof tmax(o))$이 $\beta$ 보다 작은 3D Gaussian들이 선택된다. 마지막으로, 선택된 3D Gaussian의 객체 코드를 중심 좌표와 함께 클러스터링을 위해 KNN에 입력한다. 3D Gaussian 쿼리의 경우 주변 3D Gaussian과의 거리를 계산하고 거리가 가장 가까운 $k$개의 3D Gaussian을 선택하면 쿼리 Gaussian의 개체 코드는 이러한 3D Gaussian 개체 코드의 평균으로 설정된다.
3. Gaussian Filtering
또한 저자들은 실험 과정에서 3차원 semantic 정보 학습과 Gaussian Clustering 이후 분할하려는 물체에 속하지 않는 일부 3D Gaussian이 잘못 분할되는 것을 발견했다. 저자들은 잘못 분할된 3D Gaussian이 분할된 3D Gaussian의 나머지 부분과 공간적으로 멀리 떨어져 있음을 관찰했다. 따라서 이 문제를 해결하기 위해 포인트 클라우드 segmentation에 사용된 것과 유사한 통계적 필터링 알고리즘을 사용하였다.
분할된 각 Gaussian에 대해 인접한 3D Gaussian과의 평균 거리 $D$를 계산한다. 그런 다음 이러한 평균 거리들의 평균 $\mu$와 분산 $\sigma$를 계산하고 현재 segmentation 결과에서 평균 거리 $D$가 $\mu + \sigma$ 보다 큰 3D Gaussian들을 제거한다.
Experiment
- 데이터셋: LLFF, NeRF-360, Mip-NeRF 360
- 구현 디테일
- Gaussian Clustering
- 각 3D Gaussian의 threshold $\beta$는 0.65로 설정
- 거리에 가장 가까운 50개의 3D Gaussian들이 후속 계산을 위해 필터링됨
- GPU: Nvidia Geforce RTX 3090 GPU 1개
- Gaussian Clustering
1. Result
다음은 본 논문의 방법의 정성적 결과들이다.

다음은 ISRF과 본 논문의 방법을 비교한 결과이다.

2. Ablations
다음은 ablation 결과이다.
