[논문리뷰] 2D Gaussian Splatting for Geometrically Accurate Radiance Fields

SIGGRAPH 2024. [Paper] [Page] [Github]
Binbin Huang, Zehao Yu, Anpei Chen, Andreas Geiger, Shenghua Gao
ShanghaiTech University | University of Tübingen | Tübingen AI Center
26 Mar 2024

Introduction

3D Gaussian splatting (3DGS)은 고해상도에서 실시간 novel view synthesis (NVS) 결과를 제공한다. 3DGS는 여러 도메인과 관련하여 빠르게 확장되었지만, 전체 각도의 radiance를 모델링하는 3D Gaussian이 표면의 얇은 특성과 충돌하기 때문에 복잡한 형상을 포착하는 데는 부족하다.

반면, 이전 연구에서는 surfel (surface elements)이 복잡한 형상을 효과적으로 표현하는 것으로 나타났다. 본 논문은 두 세계의 이점을 결합하고 동시에 한계를 극복하는 3D 장면 재구성 및 NVS를 위한 2D Gaussian Splatting (2DGS)을 제안하였다. 3DGS와 달리, 2DGS는 각각 방향이 있는 타원 원반을 정의하는 2D Gaussian을 사용하여 3D 장면을 표현한다. 2D Gaussian이 3D Gaussian에 비해 갖는 중요한 장점은 렌더링 중에 정확하게 형상을 표현한다는 것이다.

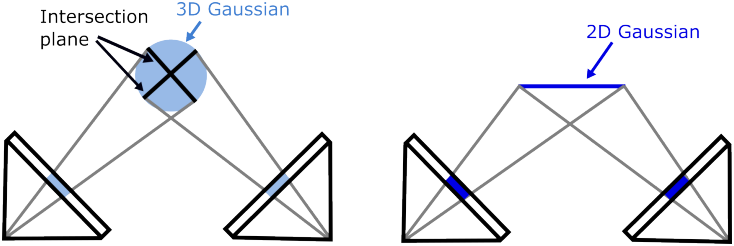
구체적으로, 3DGS는 픽셀 광선과 3D Gaussian의 교차점에서 Gaussian 값을 평가하는데, 이는 다른 관점에서 렌더링할 때 깊이가 달라진다. 반면에, 2DGS는 광선과 2D Gaussian의 명시적인 교차점을 활용하여 원근감이 정확한 splatting을 생성하여 재구성 품질을 크게 향상시킨다. 더욱이, 2D Gaussian의 고유한 normal은 normal 제약을 통해 직접적인 표면 정규화를 가능하게 한다.

2DGS는 기하학적 모델링에 뛰어나지만, RGB loss만으로 최적화하면 3D 재구성의 본질적인 특성으로 인해 노이즈가 많은 재구성으로 이어질 수 있다. 재구성을 향상시키고 더 매끄러운 표면을 얻기 위해 두 가지 정규화 항을 도입했다.

1. Depth distortion: 광선을 따라 좁은 범위 내에 분포된 2D Gaussian을 집중시켜 Gaussian 간의 거리가 무시되는 렌더링 프로세스의 한계를 해결한다.
2. Normal consistency: 렌더링된 normal map과 렌더링된 깊이의 gradient 간의 불일치를 최소화하여 깊이와 normal로 정의된 형상 간의 정렬을 보장한다.

이러한 정규화를 2D Gaussian 모델과 함께 사용하면 매우 정확한 표면 메쉬를 추출할 수 있다.

Method

1. Modeling

전체 각도의 radiance를 모델링하는 3DGS와 달리, 본 논문은 3D 공간에 포함된 평평한 2D Gaussian을 채택하여 3차원 모델링을 단순화하였다. 2D Gaussian을 사용하면 평면 원반 내에 밀도가 분포하여 normal을 가장 가파른 밀도 변화 방향으로 정의할 수 있다. 이를 이용하면 얇은 표면과 더 나은 정렬이 가능하다.

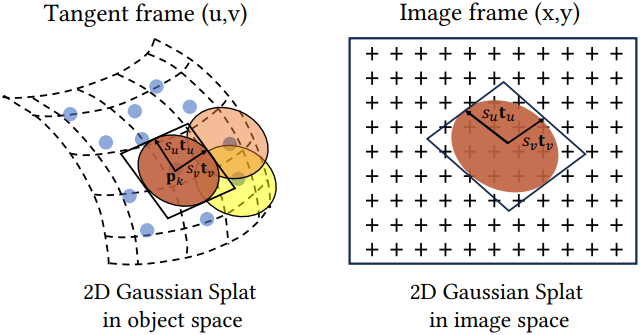
위 그림에서 볼 수 있듯이, 2D splat은 중심 \(\textbf{p}_k\), 두 개의 주 접선 벡터 \(\textbf{t}_u\)와 \(\textbf{t}_v\), 그리고 2D Gaussian의 분산을 제어하는 ​​scaling 벡터 $\textbf{S} = (s_u, s_v)$로 특징지어진다. Normal은 \(\textbf{t}_w = \textbf{t}_u \times \textbf{t}_v\)로 정의된다. 2D splat의 방향을 $3 \times 3$ 회전 행렬 \(R = [\textbf{t}_u, \textbf{t}_v, \textbf{t}_w]\)로, scaling factor를 마지막 entry가 0인 $3 \times 3$ 대각 행렬 $\textbf{S}$로 정의할 수 있다.

따라서 2D Gaussian은 다음과 같이 world space의 local tangent plane에서 정의된다.

\[\begin{equation} P(u, v) = \textbf{p}_k + s_u \textbf{t}_u u + s_v \textbf{t}_v v = \textbf{H} (u,v,1,1)^\top \\ \textrm{where} \; \textbf{H} = \begin{bmatrix} s_u \textbf{t}_u & s_v \textbf{t}_v & \textbf{0} & \textbf{p}_k \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \textbf{RS} & \textbf{p}_k \\ \textbf{0} & 1 \end{bmatrix} \end{equation}\]

($\textbf{H} \in \mathbb{R}^{4 \times 4}$는 homogeneous transformation matrix)

$uv$ space의 점 $\textbf{u} = (u, v)$에 대해 2D Gaussian 값은 표준 Gaussian으로 평가할 수 있다.

\[\begin{equation} \mathcal{G} (\textbf{u}) = \exp \left( - \frac{u^2 + v^2}{2} \right) \end{equation}\]

\(\textbf{p}_k\), $(s_u, s_v)$, \((\textbf{t}_u, \textbf{t}_v)\)는 모두 학습 가능한 파라미터이다. 3DGS를 따라, 각 2D Gaussian은 불투명도 $\alpha$와 spherical harmonics로 parameterize된 뷰에 따른 색상 $\textbf{c}$를 갖는다.

2. Splatting

2D splat을 image plane에 projection하는 것은 homogeneous coordinate에서 일반적인 2D-2D 매핑으로 설명할 수 있다. $\textbf{W} \in \mathbb{R}^{4 \times 4}$를 world space에서 screen space으로의 변환 행렬이라고 하자. 그러면 screen space에서의 점은 다음과 같이 얻을 수 있다.

\[\begin{equation} \textbf{x} = (xz, yz, z, 1)^\top = \textbf{W} P(u,v) = \textbf{W} \textbf{H} (u,v,1,1)^\top \end{equation}\]

여기서 $\textbf{x}$는 카메라에서 방출되어 픽셀 $(x, y)$를 통과하고 깊이 $z$에서 splat과 교차하는 homogeneous ray이다. 2D Gaussian을 rasterization하는 단순한 방법은 \(\textbf{M} = (\textbf{WH})^{-1}\)을 사용하여 원뿔을 screen space에 projection하는 것이다. 그러나 2D Gaussian을 측면에서 보는 경우에는 splat이 선분이 되어 역변환이 수치적 불안정성을 초래한다. 이 문제를 해결하기 위해 이전 방법들은 미리 정의된 threshold를 사용하여 이러한 조건이 나쁜 변환을 버렸다. 그러나 이러한 방식은 불안정한 최적화로 이어질 수 있으므로 미분 가능한 렌더링 프레임워크 내에서 문제가 된다.

이 문제를 해결하기 위해 본 논문은 광선과 splat의 명시적인 교차점을 활용한다.

Ray-splat Intersection

세 개의 서로 평행하지 않은 평면의 교차점을 찾음으로써 광선과 splat의 교차점을 효율적으로 찾는다. 이미지 좌표 $\textbf{x} = (x, y)$가 주어지면 해당 픽셀의 광선을 두 직교 평면, 즉 $x$ 평면과 $y$ 평면의 교차점으로 나타낼 수 있다.

구체적으로, $x$ 평면은 normal 벡터 $(-1, 0, 0)$과 offset $x$로 정의된다. 따라서 $x$ 평면은 4D homogeneous plane \(\textbf{h}_x = (-1, 0, 0, x)^\top\)로 표현할 수 있다. 마찬가지로 $y$ 평면은 \(\textbf{h}_y = (0, -1, 0, y)^\top\)이다. 따라서 $\textbf{x} = (x, y)$는 $x$ 평면과 $y$ 평면의 교차점에 의해 결정된다.

다음으로, $x$ 평면과 $y$ 평면을 모두 2D Gaussian의 로컬 좌표인 $uv$ 좌표계로 변환한다. 변환 행렬 $\textbf{M}$을 사용하여 평면의 점을 변환하는 것은 $\textbf{M}^{-\top}$를 사용하여 homogeneous plane의 파라미터를 변환하는 것과 동일하다. $\textbf{M} = (\textbf{WH})^{-1}$이므로 다음을 얻는다.

\[\begin{aligned} \textbf{h}_u = (\textbf{WH})^\top \textbf{h}_x = (h_u^1, h_u^2, h_u^3, h_u^4)^\top \\ \textbf{h}_v = (\textbf{WH})^\top \textbf{h}_y = (h_v^1, h_v^2, h_v^3, h_v^4)^\top \end{aligned}\]

2D Gaussian 평면의 점은 $(u,v,1,1)$로 표현된다. 동시에, 교점점은 변환된 $x$ 평면과 $y$ 평면에 있어야 한다. 따라서 다음 식이 성립한다.

\[\begin{equation} \textbf{h}_u \cdot (u,v,1,1)^\top = \textbf{h}_v \cdot (u,v,1,1)^\top = 0 \end{equation}\]

이 식을 풀면 교차점 $\textbf{u}(\textbf{x}) = (u(\textbf{x}), v(\textbf{x}))$에 대한 해를 구할 수 있다.

\[\begin{equation} u(\textbf{x}) = \frac{h_u^2 h_v^4 - h_u^4 h_v^2}{h_u^1 h_v^2 - h_u^2 h_v^1} \quad v(\textbf{x}) = \frac{h_u^4 h_v^1 - h_u^1 h_v^4}{h_u^1 h_v^2 - h_u^2 h_v^1} \end{equation}\]

Degenerate Solutions

2D Gaussian을 기울어진 시점에서 보면 screen space에서는 선으로 보인다. 따라서 이러한 2D Gaussian은 rasterization 중에 놓칠 수 있다. 이러한 경우를 처리하고 최적화를 안정화하기 위해 object-space low-pass filter를 사용한다.

\[\begin{equation} \hat{\mathcal{G}} (\textbf{x}) = \max \left\{ \mathcal{G} (\textbf{u}(\textbf{x})), \mathcal{G} (\frac{\textbf{x} - \textbf{c}}{\sigma}) \right\} \end{equation}\]

($\textbf{c}$는 중심 $\textbf{p}_k$의 projection)

직관적으로 \(\hat{\mathcal{G}} (\textbf{x})\)는 중심이 $\textbf{c}$이고 반지름이 $\sigma$인 고정된 screen space Gaussian low-pass filter로 하한이 설정된다. 저자들은 렌더링 중에 충분한 픽셀이 사용되도록 $\sigma = \sqrt{2}/2$로 설정했다.

Rasterization

2DGS는 3DGS와 유사한 rasterization 프로세스를 따른다. 먼저, 각 Gaussian에 대해 screen space bounding box가 계산된다. 그런 다음, 2D Gaussian들은 중심의 깊이를 기준으로 정렬되며, bounding box를 기반으로 타일로 구성된다. 마지막으로, 알파 블렌딩을 사용하여 앞에서 뒤로 색상을 통합한다.

\[\begin{equation} \omega_i = \alpha_i \hat{\mathcal{G}}_i (\textbf{u} (\textbf{x})) \prod_{j=1}^{i-1} (1 - \alpha_j \hat{\mathcal{G}}_j (\textbf{u} (\textbf{x}))) \\ \textbf{c} (\textbf{x}) = \sum_{i=1} \textbf{c}_i \omega_i \end{equation}\]

이 프로세스는 누적된 불투명도가 포화 상태에 도달하면 종료된다.

3. Training

2DGS는 형상 모델링에 효과적이지만 RGB loss로만 최적화할 경우 노이즈가 많은 재구성을 초래할 수 있으며, 이 문제를 완화하고 기하학적 재구성을 개선하기 위해 depth distortion과 normal consistency라는 두 가지 정규화 항이 도입되었다.

Depth Distortion

3DGS의 볼륨 렌더링은 교차된 Gaussian 사이의 거리를 고려하지 않는다. 따라서 Gaussian을 퍼뜨려도 유사한 색상과 깊이 렌더링을 얻을 수 있다. 저자들은 이 문제를 완화하기 위해 Mip-NeRF360에서 영감을 얻어 교차점 사이의 거리를 최소화하여 가중치 분포를 집중시키는 depth distortion loss를 제안하였다.

\[\begin{equation} \mathcal{L}_d = \sum_{i,j} \omega_i \omega_j \vert z_i - z_j \vert \end{equation}\]

(\(\omega_i\)는 $i$번째 교차점의 알파 블렌딩 가중치, $z_i$는 교차점의 깊이)

Mip-NeRF360의 distortion loss는 $z_i$가 샘플링된 포인트 사이의 거리이고 최적화되지 않는 반면, \(\mathcal{L}_d\)는 $z_i$를 조정하여 splat의 집중을 직접적으로 촉진한다.

Normal Consistency

2DGS의 표현은 2D Gaussian surfel에 기반을 두고 있으므로 모든 2D splat이 실제 표면과 로컬하게 정렬되도록 해야 한다. 여러 개의 반투명 surfel이 광선을 따라 존재할 수 있는 볼륨 렌더링의 맥락에서, 누적 불투명도가 0.5에 도달하는 중간 교차점 \(\textbf{p}_s\)를 실제 표면을 고려한다. 그런 다음 splat의 normal을 다음과 같이 depth map의 gradient와 정렬한다.

\[\begin{equation} \mathcal{L}_n = \sum_i \omega_i (1 - \textbf{n}_i^\top \textbf{N}) \end{equation}\]

구체적으로, depth map의 gradient로 추정된 normal $\textbf{N}$은 다음과 같이 계산된다.

\[\begin{equation} \textbf{N} (x,y) = \frac{\nabla_x \textbf{p}_s \times \nabla_y \textbf{p}_s}{\vert \nabla_x \textbf{p}_s \times \nabla_y \textbf{p}_s \vert} \end{equation}\]

Splat의 normal을 depth map에서 추정된 normal과 정렬함으로써 2D splat이 실제 물체 표면에 로컬하게 근사되도록 한다.

Final Loss

전체 loss function은 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_c + \alpha \mathcal{L}_d + \beta \mathcal{L}_n \end{equation}\]

(\(\mathcal{L}_c\)는 \(\mathcal{L}_1\)과 D-SSIM 항을 결합한 3DGS의 RGB reconstruction loss)

Experiments

• 데이터셋: DTU, Tanks and Temples, Mip-NeRF360
• 구현 디테일
  • 3DGS의 커스텀 CUDA 커널을 기반으로 구현
  • 3DGS와 동일한 adaptive control 전략을 사용하여 Gaussian의 수를 조절
  • Projection된 2D 중심의 gradient에 직접적으로 의존하지 않기 때문에, 대신 3D 중심 \(\textbf{p}_k\)의 gradient를 screen space에 projection하여 근사값으로 사용
  • gradient threshold: 0.0002
  • 3,000 step 마다 0.05보다 불투명도가 작은 splat을 제거
  • GPU: RTX3090 GPU 1개
  • $\alpha$: bounded scene은 1000, unbounded scene은 100
  • $\beta$: 0.05
• 메쉬 추출
  • Depth map을 렌더링한 뒤, Open3D의 TSDF fusion으로 메쉬를 추출
  • voxel size: 0.004
  • truncated threshold: 0.02

1. Comparison

다음은 렌더링된 이미지, normal, 추출한 메쉬를 정성적으로 비교한 것이다.

다음은 DTU 데이터셋에서 Chamfer distance (CD)를 비교한 표이다.

다음은 DTU 데이터셋에서 평균 CD, PSNR, 재구성 시간, 모델 크기를 비교한 표이다.

다음은 DTU 데이터셋에서 추출한 메쉬를 정성적으로 비교한 것이다.

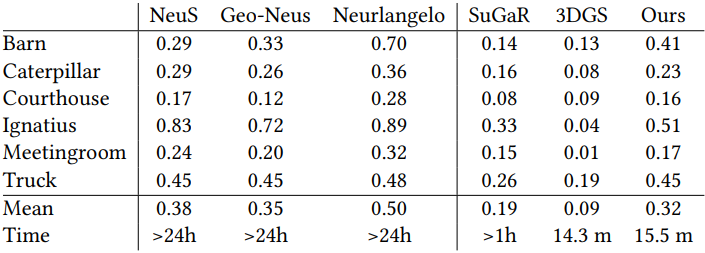
다음은 Tanks and Temples 데이터셋에서 F1 score와 학습 시간을 비교한 표이다.

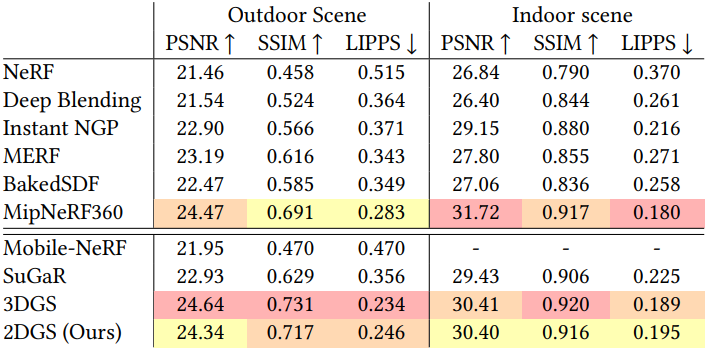
다음은 Mip-NeRF 360 데이터셋에서 렌더링 품질을 비교한 표이다.

2. Ablations

다음은 ablation 결과이다.