[RL공부] 1. Exact Dynamic Programming (Reinforcement Learning and Optimal Control - Bertsekas, MIT)
이 책의 가장 중요한 점은 강화학습을 optimal control 문제로 생각한다는 것이다. 그리고 optimal control 문제를 풀기 위해서 Dynamic Programming (DP)을 사용한다. DP로 강화학습 문제를 정의하는 것이 이 책 1장의 주요 내용이다. 2장부터는 강화학습 문제를 세분화하고 DP로 정의한 문제를 효율적으로 빠르게 풀기 위하여 문제를 근사하여 더 쉽게 만드는 다양한 접근법을 설명한다. 아래의 내용은 1장에 대한 내용만 다루었다.
1.1 Deterministic Dynamic Programming
1.1.1 Deterministic Problem
먼저 deterministic problem에 대하여 살펴보자. Deterministic problem은 아래와 같은 이산 시간의 동적 시스템으로 나타낼 수 있다.
\[\begin{equation} x_{k+1} = f_k (x_k, u_k), \quad \quad k = 0, 1, \cdots, N - 1 \end{equation}\]$k$는 시간 인덱스, $x_k$는 시스템의 상태, $u_k$는 control 혹은 decision variable이다. 상태 $x_k$에서 가능한 전체 control을 포함하는 집합을 $U_k (x_k)$라 표현할 수 있다.
Control $u_k$에 의해 $x_k$에서 $x_{k+1}$로 가는 과정을 “Stage $k$”라고 하며, stage $k$에서 stage cost $g_k (x_k, u_k)$라 발생한다.
가능한 모든 $x_k$의 집합을 시간 $k$에서의 state space라 부르며, $x_k$는 state space의 element이다.
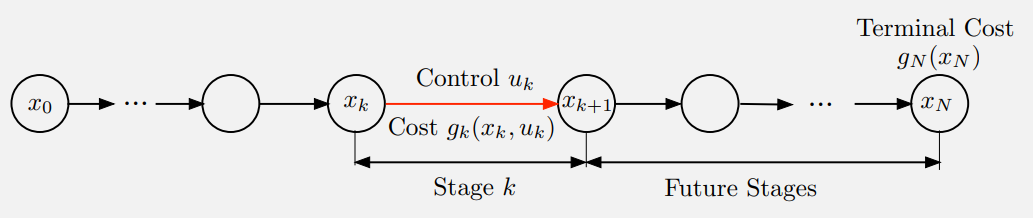
주어진 초기 state $x_0$에 대하여, control sequence \(\{u_0, \cdots, u_{N-1}\}\)이 정해지면 deterministic하게 state sequence \(\{x_1, \cdots, x_N\}\)가 정해지고 마지막 state $x_N$에 도착한다. $x_N$에서는 terminal cost $g_N (x_N)$이 존재하며, 일반적으로 어떤 control sequence를 선택하여도 마지막에는 state $x_N$에 도착한다.
이 때, 주어진 $x_0$와 control sequence의 전체 cost는 다음과 같다.
\[\begin{equation} J(x_0; u_0, \cdots, u_{N-1}) = g_N (x_N) + \sum_{k=0}^{N-1} g_k (x_k, u_k) \end{equation}\]우리가 원하는 것은 모든 control sequence에 대하여 이 전체 cost를 최소화하여 optimal value
\[\begin{equation} J^\ast (x_0) = \min_{u_k \in U_k (x_k) \\ k = 0, \cdots, N-1} J(x_0; u_0, \cdots, u_{N-1}) \end{equation}\]을 얻는 것이며, optimal value는 $x_0$의 함수이다.
1.1.2 The Dynamic Programming Algorithm
Principle of Optimality
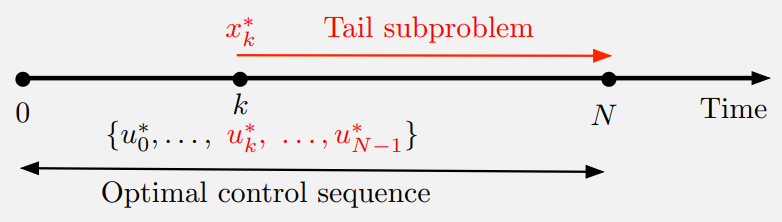
\(\{u_0^\ast, \cdots, u_{N-1}\ast \}\)가 $x_0$와 함께 state sequence \(\{x_1^\ast, \cdots, x_N^\ast\}\)를 결정하는 optimal control sequence이라 하자. $x_k^\ast$에서 시작하는 subproblem은 $k$에서 $N$까지의 “cost-to-go”
\[\begin{equation} g_k (x_k^\ast, u_k) + \sum_{m = k+1}^{N-1} g_m (x_m, u_m) + g_N (x_N) \end{equation}\]를 최소화하는 문제이다. 그러면 truncated optimal control sequence \(\{u_k^\ast, \cdots, u_{N-1}^\ast\}\)는 이 subproblem에 optimal이다.
즉, optimal sequence의 tail은 tail subproblem에 optimal이다.
Principle of Optimality에 의해 optimal cost function을 거꾸로 진행되는 방식으로 계산할 수 있게 된다. 가장 먼저 마지막 stage를 포함하는 tail subproblem의 optimal cost function을 계산한다. 그런 다음 마지막 2개의 stage를 포함하는 tail subproblem의 optimal cost function을 계산한다. 이를 전체 problem의 optimal cost function을 계산할 때까지 계속 진행하는 것이다.
DP 알고리즘은 이 아이디어를 기반으로 하여 $J_N^\ast (x_N), J_{N-1}^\ast (x_{N-1}), \cdots, J_0^\ast (x_0)$ 순서로 진행된다.

DP 알고리즘의 핵심 사실은 모든 $x_0$에 대하여 마지막 step에 얻어지는 $J_0^\ast (x_0)$가 optimal cost $J^\ast (x_0)$와 같다는 것이다. 또한, 더 일반적인 사실은 모든 $k = 0, 1, \cdots, N-1$과 모든 state $x_k$에 대하여
이라는 것이다. 여기서 $J_k^\ast (x_k)$는 $(N-k)$-stage tail subproblem의 optimal cost이다.
$J_0^\ast, \cdots, J_N^\ast$가 얻어지면, 주어진 $x_0$에 대하여 아래의 알고리즘을 사용하여 optimal control sequence \(\{u_0^\ast, \cdots, u_{N-1}^\ast\}\)를 구성할 수 있으며, 대응되는 state trajectory \(\{x_1^\ast, \cdots, x_N^\ast\}\)를 구성할 수 있다.

같은 알고리즘을 사용하여 임의의 tail subproblem의 optimal control sequence를 찾을 수 있다.
1.1.3 Approximation in Value Space
Optimal Control sequence는 모든 $k$와 $x_k$에 대하여 $J_k^\ast (x_k)$를 계산한 후에만 구성할 수 있다. 불행히도 실제로는 가능한 $k$와 $x_k$의 수가 굉장히 커서 계산에 시간이 굉장히 오래 걸린다.
한편, optimal cost-to-go function $J_k^\ast$를 어떤 근사 $\tilde{J}_k$로 대체하면 비슷한 forward 알고리즘을 사용할 수 있다. 이것이 approximation in value space의 토대이다. \(\{u_0^\ast, \cdots, u_{N-1}^\ast\}\)을 \(\{\tilde{u}_0, \cdots, \tilde{u}_{N-1}\}\)로 대체하고 $J_k^\ast$를 $\tilde{J}_k$로 대체한다.

적합한 $\tilde{J}_k$를 구성하는 것이 RL 방법론의 주요 목표이다.
Q-Factors and Q-Learning
$(x_k, u_k)$의 Q-factor를 다음과 같이 정의한다.
\[\begin{equation} \tilde{Q}_k (x_k, u_k) = g_k (x_k, u_k) + \tilde{J}_{k+1} (f_k (x_k, u_k)) \end{equation}\]Approximately optimal control의 계산은 Q-factor 최소화로 표현할 수 있다.
\[\begin{equation} \tilde{u}_k \in \underset{u_k \in U_k(\tilde{x}_k)}{\arg \min} \tilde{Q}_k (\tilde{x}_k, u_k) \end{equation}\]Approximation in value space 방식에서 cost function 대신 Q-factor를 사용할 수 있다. Q-factor를 사용하면 DP 알고리즘의 대체 형태를 사용해야 하며 $J_k^\ast$ 대신 optimal Q-factor $Q_k^\ast$를 사용해야 한다.
\[\begin{equation} Q_k^\ast (x_k, u_k) = g_k (x_k, u_k) + J_{k+1}^\ast (f_k (x_k, u_k)) \end{equation}\]따라서 optimal Q-factor는 DP 방정식의 표현을 간단하게 만든다.
\[\begin{equation} J_k^\ast (x_k) = \min_{u_k \in U_k (x_k)} Q_k^\ast (x_k, u_k) \end{equation}\]또한, DP 알고리즘은 Q-factor를 포함하여 아래와 같이 표현할 수 있다.
\[\begin{equation} Q_k^\ast (x_k, u_k) = g_k (x_k, u_k) + \min_{u_{k+1} \in U_{k+1}(f(x_k, u_k))} Q_{k+1}^\ast (f_k (x_k, u_k), u_{k+1}) \end{equation}\]1.2 Stochastic Dynamic Programming
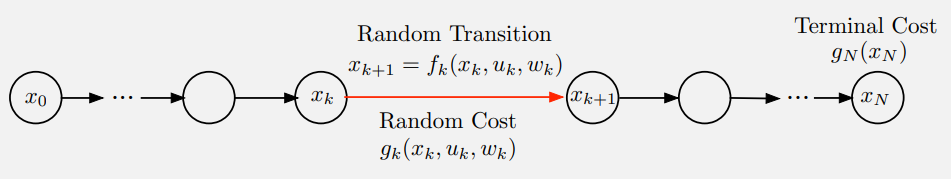
Stochastic finite horizon optimal control problem은 deterministic한 버전과 다르다. 이 시스템은 랜덤 “disturbance” $w_k$를 포함하며, $w_k$는 $x_k$와 $u_k$에 의존하는 확률 분포를 따르며, disturbance들은 서로 독립적이다. 시스템은 아래와 같은 형태로 나타낸다.
Cost도 $g_k(x_k, u_k, w_k)$로 나타낸다.
Deterministic한 버전과의 가장 중요한 차이점은 control sequence \(\{u_0, cdots, u_{n-1}\}\)가 아닌 policy
\(\begin{equation} \pi = \{\mu_0, \cdots, \mu_{N-1}\} \end{equation}\) 을 통해 최적화한다는 것이다. $\mu_k$는 $x_k$를 control $u_k = \mu_k (x_k)$로 매핑하는 함수이며 control constraints $\mu_k (x_k) \in U_k (x_k)$를 만족한다. 이러한 policy들을 admissible policy라 한다.
또다른 중요한 차이점은 stochastic한 버전의 경우 cost function과 같은 여러 값들을 기대값 형태로 평가해야 한다는 것이다.
$x_0$와 $\pi$가 주어지면 $x_k$와 $w_k$는 시스템 방정식
\[\begin{equation} x_{k+1} = f_k (x_k, \mu_k (x_k), w_k), \quad \quad k = 0, 1, \cdots, N-1 \end{equation}\]의 랜덤 변수이다. 따라서 $g_k$가 주어지면 $x_0$에서 시작하는 $\pi$의 expected cost는
\[\begin{equation} J_\pi (x_0) = \mathbb{E}_{w_k} \bigg[ g_N (x_N) + \sum_{k=0}^{N-1} g_k (x_k, \mu_k (x_k), w_k) \bigg] \end{equation}\]이다. Optimal policy $\pi^\ast$는 위의 expected cost를 최소화하는 policy이다.
\[\begin{equation} J_{\pi^\ast} (x_0) = \min_{\pi \in \Pi} J_\pi (x_0) \end{equation}\]$\Pi$는 모든 admissible policy들의 집합이다.
Finite Horizon Stochastic Dynamic Programming
Stochastic한 버전의 DP 알고리즘은 deterministic한 버전과 비슷하다.

(* 책에서는 $\mathbb{E}_{w_k}$ 대신 $E$로 표현)
Deterministic한 버전과 마찬가지로 모든 $x_0$에 대하여 마지막 step에 얻어지는 $J_0^\ast (x_0)$가 optimal cost $J^\ast (x_0)$와 같다.
또한 기대값을 계산해야 하기 때문에 deterministic한 버전보다 더 시간이 오래 걸린다. 따라서 $J_k^\ast$ 대신 얻기 쉬운 $\tilde{J}_k$로 대체된 suboptimal control 테크닉을 사용한다.
Q-Factors for Stochastic Problems
Deterministic problem과 비슷하게 optimal Q-factor를 정의할 수 있다.
\[\begin{equation} Q_k^\ast (x_k, u_k) = \mathbb{E}_{w_k} \bigg[ g_k (x_k, u_k, w_k) + J_{k+1}^\ast (f_k (x_k, u_k, w_k)) \bigg] \end{equation}\]$J_k^\ast$는 optimal Q-factor $Q_k^\ast$로 바꿀 수 있다.
\[\begin{equation} J_k^\ast (x_k) = \min_{u_k \in U_k (x_k)} Q_k^\ast (x_k, u_k) \end{equation}\]또한, DP 알고리즘은 Q-factor 항으로 다시 쓸 수 있다.
\[\begin{aligned} Q_k^\ast (x_k, u_k) =& \mathbb{E}_{w_k} \bigg[ g_k (x_k, u_k, w_k) \\ &+ \min_{u_{k+1} \in U_{k+1}(f(x_k, u_, w_k))} Q_{k+1}^\ast (f_k (x_k, u_k, w_k), u_{k+1}) \bigg] \end{aligned}\]